Таблицы объема и сбега древесных стволов.

Таксационные показатели насаждения и их определение.

На продольном разрезе ствола хорошо заметно последовательное уменьшение диаметра ствола от его основания к вершине. Изменение величины диаметра ствола приходящееся на единицу его длины называется сбегом. Его величина в разных частях одного и того же ствола различна: наименьшая – в средней части ствола, наибольшая – в области корневых наплывов и верхней части ствола. Различают его следующие виды:

- абсолютный (действительный)-изменение диаметра ствола в сантиметрах на протяжении всей длины ствола от основания до вершины через определенные интервалы (1,2ми т.д.). Дает возможность наглядно представить форму ствола. Является основным таксационным признаком ствола. Лежит в основе получения математических моделей определения объема ствола.

- относительный - выражает диаметры по длине ствола в процентах от принятого исходного диаметра. Обычно за 100% берут диаметр на высоте груди или на 0,1Н.

- средний - представляет разность между диаметром в нижнем D_н и верхнем D_в отрезах, разделенную на длину бревна L: 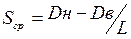. Иногда определяется и для целого ствола путем деления диаметра ствола на высоте груди на длину ствола, уменьшенную на 1,3 м.

Относительный сбег стволов по относительным высотам обычно выражают через коэффициенты формы. Этот способ впервые был предложен Шиффелем на рубеже XIX-XX веков в виде четырех коэффициентов формы (q_n).

Они представляют отношение диаметров на относительных высотах (0,25Н; 0,50Н; 0,75Н), к диаметру на высоте 1,3 м.

Наибольшее использование в лесной таксации приобрела величина q₂(q₂=d_0,5 : d_1,3), называемая вторым коэффициентом формы. Она характеризует степень сбежистости нижней половины стволов.

Проф. Н.В. Третьяков выдвинул иной показатель сбежистости ствола, названный им классом формы.Он представляет собой отношения диаметров на относительных высотах 1/2Н к диаметру на 1/4Н и 3/4Н к диаметру на 1/4Н.

Такие показатели лучше отражают действительную форму ствола, чем коэффициенты формы, вычисленные через диаметры на высоте 1,3 м..

По величинам q_2/1 и q₂ определяют сбежистость стволов при этом различают три градации:

q_2/1 = 0,75 — стволы сильносбежистые; q₂ = 0,55¸0,60

q_2/1 = 0,80 — стволы среднесбежистые; q₂ =0,65¸0,70

q_2/1 = 0,85 — стволы малосбежистые; q₂=0,75¸0,80.

Применяя эти показатели к правильным телам вращения с постоянной формой, получаем константные значения q_2/1 и q_3/1. Вычисляя эти показатели для тел вращения образующей ствола получаем:

для параболоида 2-го порядка q_2/1 = 0,815;

для конуса q_2/1 = 0,675;

нейлоида q_2/1 = 0,545.

Если для этих же тел взять отношения диаметров на высоте 1/2Н к диаметру при основании, т. е. d_1/2 : d₀ = q_1/0, то получим для цилиндра q_1/0=1,00; параболоида q_1/0=0,707; конуса q_1/0=0,500; нейлоида q_1/0=0,354.

Различают стволы сбежистые, полнодревесные и средней формы (с наличием многих переходных форм между этими группировками). Деревья, растущие на просторе, характеризуются большой сбежистостью, в то время как деревья в составе насаждения являются более полнодревесными. При одинаковых диаметрах на высоте 1,3 м и высотах объемы отдельных деревьев различны, что обусловливается различиями их формы.

Для установления объема ствола на основе величины диаметра на высоте 1,3 м и высоты стоящего дерева в таксации введено понятие - видовое число f, которое представляет соотношение объема ствола с объемом одномерного цилиндра, имеющего со стволом одинаковую высоту Н и площадь сечения g, взятую на высоте 1,3 м. Это соотношение получило название «старого видового числа» (от немецкого слова Formzahl) и определяется математически следующим соотношнием: 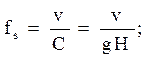. Откуда v = Cf_s = gHf =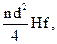

где: v — объем ствола; С — объем одномерного цилиндра.

Из формулы видно, что объем ствола равен произведению объема цилиндра на видовое число. Таким образом, видовое число является переводным коэффициентом для перехода от объема цилиндра к объему ствола.

Таким же образом вычисляется видовое число для всего дерева, т.е. объема ствола с кроной f_B =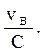

Разность между видовыми числами объема дерева f_B и объема стволa fs составит видовое число объема сучьев fa, т.е. fa - f_B = fs.

Закономерности изменения видовых чисел и коэффициентов формы. Исходя из формы древесного ствола, отвечающей форме параболоида 2-го порядка формула видового числа выражается в следующем виде:

f= ,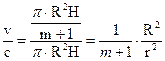

где: R - радиус параболоида при основании;

r - радиус параболоида на высоте 1,3 м,

m - показатель степени, характеризующий форму образующей (для параболоида m=1). После преобразований получаем: f =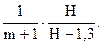

Изменение m в формуле характеризует особенности образующей ствола. Допуская постоянной высоту дерева видим, что при увеличении «m» - видовое число уменьшается, (то есть полнодревесность падает). При уменьшении m наоборот увеличивается.

Если допустить неизменным форму ствола (m = константа), то с увеличением Н видовое число уменьшается.

Обратная зависимость среднего видового числа от высоты Hпри неизменности формы выражается графически кривой, имеющей вид гиперболы, которая характеризуется уравнением общего вида: f = a +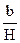

Старое видовое число, будучи в зависимости от H, не может характеризовать формы древесных стволов.

Закономерности изменения видовых чисел и коэффициентов формы. Многочисленные расчеты таксаторов показывают, что численное значение соотношения 1,3:Н лежит в пределах 0,03-0,1 в среднем принимая значение около 0,05. Тогда если в формулу вместо постоянной величины 1,3 и переменного отношения 1,3: Н ввести постоянную величину 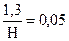, то она примет следующий вид: f = 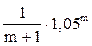, а при измерении диаметра на 0,1Н, формула примет вид f_n = 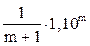, т.е. величина f_n обусловливается лишь влиянием формы ствола и не зависит от H.

Видовые числа, полученные по этой формуле и предложенные в 1873 г. Пресслером, получили название нормальных видовых чисел.

Нормальное видовое число f не зависит от H и остается неизменным при одинаковой форме стволов (в отношении правильных тел вращения). Так, для параболоида при всех высотах f=0,526, для конуса f=0,368, для нейлоида f=0,289.

Проф. В.К. Захаровым, было установлено, что при выражении коэффициентов формы в относительных единицах по наблюдаемым древесным породам среднее f_n приобретает значение постоянной величины, вычисляемой по формуле: f_n = 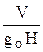, откуда объем ствола V = g_0,1 Hf_{n .}

Среднее значение f_n (по данным кафедры таксации БТИ, Минск) составляет для стволов сосны в коре 0,520, без коры 0,538, для ели соответственно 0,540 и 0,547, т.е. варьирование f_n небольшое (2,31- 4,60%). Распределение числа стволов по индивидуальным f_n характеризуется кривой нормального распределения.

Используя тесную взаимосвязь диаметра на высоте груди и диаметра на 0,1 Н переходим к диаметру на 0,1 Н.

Использовать нормальные видовые числа удобнее всего через видовые высоты (Hf_n). При постоянной величине средних f_n по породам составление таблиц для Hf_nне представляет особых затруднений.

В 1894г. Шпейдель рекомендовал способ использования абсолютных видовых чисел. Он предложил построить цилиндр, с которым следовало сопоставлять объем ствола не на площади сечения на высоте 1,3 м, а на основании ствола вычислять его диаметр d₀ по d_1,3 исходя из основного свойства образующей параболоида: квадраты диаметров относятся между собой как соответствующие им высоты, т.е.

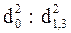= H: (Н-1,3), откуда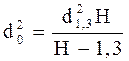

С этой целью были составлены вспомогательные таблицы значений d₀ по d_1,3 и Н. Положительной стороной абсолютного видового числа является то, что при одинаковой высоте ствола и диаметре на высоте 1,3 м оно отражает различия формы стволов. Тем не менее в практике абсолютные видовые числа не получили применения: вследствие необходимости дополнительных вычислений d₀ даже при использовании готовых таблиц. Еще менее приемлемым для практического использования оказалось предложение Риникера получать видовые числа делением объема ствола выше 1,3 мна объем цилиндра той же высоты. По этому способу объем нижней секции длиной 1,3 м нужно было бы определять дополнительно.

Таким образом, несмотря на приведенные выше недостатки старых видовых чисел, они оказались наиболее приемлемыми и прочно вошли в теорию и практику лесной таксации.

Проведенные исследования старых видовых чисел позволили впервые в Баварии (1846 г.) разработать таблицы средних видовых чисел и использовать их для составления первых таблиц объемов растущих стволов, известных под названием баварских.

Для их составления были использованы обмеры свыше 40 тысяч стволов разных древесных пород. Баварские таблицы видовых чисел как средних величин были составлены по породам, ступеням толщины и высотам. Кроме того, были приняты три группы возрастов: до 60 лет, от 61 до 90 лет и старше 91 года. Полученные средние величины по приведенным группам обмеров сглаживались простейшим графическим способом.

Баварские таблицы объемов, несмотря на местный характер, на протяжении почти полстолетия были единственными и нашли успешное применение и за пределами Баварии, в том числе в царской России (1869-1886).

По образцу баварских таблиц немецкими опытными станциями в конце XIX столетия был составлен ряд таблиц средних видовых чисел, а на основе их — таблицы объемов древесных стволов.

Видовые числа древесных стволов, характеризующие соотношения объемов ствола и одномерного цилиндра, дают относительное представление о полнодревесности стволов. Для характеристики формы древесных стволов, отражающей их сбег Шиффель (1899) предложил для этой цели принимать соотношения диаметров ствола, измеренных на разных высотах — у основания, на 1/4Н, 1/2Н и 3/4Н — к диаметру на высоте 1,3 м.

Эти отношения были названы коэффициентами формы

q₀ = 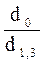; q₁ = 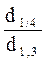; q₂ = 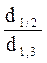; q₃ = .

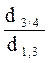Анализируя величины этих коэффициентов и их соотношения, Шиффель установил, что величины q₁, q₂, q₃ находятся между собой в определенной для известной высоты ствола постоянной взаимосвязи, что позволяет по одной из них определять величины двух других. В результате последующих исследований была установлена взаимосвязь коэффициентов формы q₂ с видовыми числами и высотами, выраженная эмпирическими формулами.

Простейшую взаимосвязь f и q₂ можно видеть из следующих сопоставлений.

Объем ствола по простой формуле срединного сечения равен: V = g H.

Объем одномерного цилиндра C = g_1,3 H,

где q_1,3 — площадь сечения на высоте 1,3 м..

Отсюда видовое число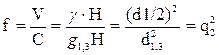

где d _½ - диаметр ствола на половине высоты.

Это приближенная формула Вейзе.

Таким образом, видовое число f равно квадрату коэффициента формы g₂. Следовательно, точность величины f по этому способу обусловливается точностью определения объема стволов по простой формуле срединного сечения и в отношении отдельных стволов может давать отклонения до ±10% и больше. Если брать средние величины f для нескольких стволов, то может быть полученаболее удовлетворительная точность.

Кунце (1891) при изучении закономерностей изменения видовых чисел также исходил из отношений диаметров d _1/2 и d_1,3, т.е. q₂ = 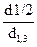, и на конкретном материале отдельных древесных пород (сосны, ели, бука) исследовал опытным путем разность между q₂ - f = C .

Было установлено, что для стволов длиной 15-18 м и более разность С является для отдельных пород величиной постоянной и составляет: для сосны 0,20; ели 0,21; бука 0,22-0,23; березы 0,22; осины 0,24; черной ольхи 0,22 и липы 0,21.

В общем виде формула для f имеет вид

f = q₂ - C.

Как показали исследования проф. А.В. Тюрина, формула Кунце дает лучшие результаты по сравнению с формулой 6.17. По исследованиям В.К. Захарова средняя величина С для отдельных пород составила следующие значения: сосна 0,211; ель 0,219; черная ольха 0,211; осина 0,217; дуб 0,197; ясень 0,200: кедр 0,207. Приведенные значения С получены на значительном экспериментальном материале и отличаются большой устойчивостью по породам.

Всеобщие таблицы видовых чисел позволяют получить уточненные значения С в зависимости от высот стволов и коэффициентов формы q₂.

Углубленные исследования видовых чисел и коэффициентов формы q₂ и зависимости их от древесных пород и высот были проведены Шиффелем в процессе составления таблиц объемов стволов лиственницы, сосны, пихты и ели. Изучая изменения видовых чисел по высотам и коэффициентам формы q₂ Шиффель пришел к выводу, что кривые изменения видовых чисел выражаются уравнением следующего общего вида: f = a + bq₂ + ,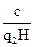

где: f — видовое число ствола; q₂ — коэффициент формы; q₂= ;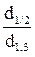

Н— высота ствола; а, b, с — некоторые постоянные коэффициенты.

Исходя из анализа экспериментального материала Шиффелем были установлены цифровые параметры приведенного уравнения и получены четыре уравнения для вычисления видовых чисел, а именно: для лиственницы, сосны, пихты, ели.

Выполнив в разное время работы по каждой породе и сопоставив значения видовых чисел по приведенным формулам, Шиффель убедился, что влияние древесной породы при одинаковых q₂, H и d_1,3 на величину видового числа и объема древесных стволов настолько незначительно, что представляется возможным пользоваться любой из приведенных формул. Для всех хвойных пород он рекомендовал в качестве общей формулу, выведенную для ели.

Таким образом, для всех древесных пород объем ствола можно вычисляют по формуле V = g_1,3H(0,14+0,66q 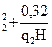. При анализе формы видовых чисел можно видеть, что величина f является функцией двух переменных величин q₂ и Н. При неизменности величины Н и повышении q₂ видовое число увеличивается. Наоборот, при одинаковых q₂ видовое число находится в обратной зависимости от Н, т.е. уменьшается.

В 1908 г. Маас (Швеция), анализируя видовые числа стволов сосны и ели в зависимости от Н и q₂ пришел к выводу, что при одинаковых Н и q₂ влияние древесной породы настолько незначительно, что позволяет составить для них единую таблицу видовых чисел.

Значения видовых чисел по классам коэффициента формы q₂

Высота,	Значения видовых чисел по классам коэффициента формы q2
м	0,60	0,65	0,70	0,75	0,80
	0,464	0,501	0,537	0,574	0,610
	0,444

В 1911 г. проф. М.Е. Ткаченко продолжил исследования Шиффеля и Мааса относительно лиственных пород и сформулировал закон формы древесных стволов.

Стволы хвойных и лиственных пород, взятые из древостоев, растущих при любых естественноисторических условиях, подчиняются одному и тому же закону формы стволов: при равных высотах, диаметрах и коэффициентах формы q₂ стволы всех древесных пород имеют близко равные видовые числа, а следовательно, и близко равные объемы. Таким образом, в таблицах М.Е. Ткаченко не учитывается влияние условий местопроизрастания на видовые числа при одинаковых высотах и коэффициентах формы q₂.

Основываясь этом проф. М.Е. Ткаченко составил таблицу всеобщих видовых чисел в зависимости от высот и коэффициентов формы q₂.

Из таблиц, приведенных М.Е. Ткаченко и Маасом, видно, что с увеличением видовых чисел повышаются значения q₂ при данной высоте и, наоборот, при одинаковых q₂ видовые числа уменьшаются при увеличении высот H..

Определение объема растущих деревьев. Как уже отмечалось нахождение объема ствола неотъемлемо от определения средней его формы. В лесотаксационной литературе среднюю форму стволов обычно выражают через средний коэффициент формы q₂.

Исследования Ф.П. Моисеенко и В.К. Захарова позволили составить объемные таблицы с учетом средней формы ствола.

В настоящее время установлены средние величины q₂ для главнейших пород: березы 0,65, сосны 0,67, дуба 0,68-0,69, ели, осины, ольхи черной, пихты 0,70. Если в формулу Шиффеля f = 0,14+0,66q ,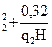

вместо q₂ подставить для данной породы абсолютную величину среднего q₂, то формула приобретет вид f = a + .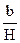

Таблица видовых чисел в зависимости от Н и q₂ (по М.Е. Ткаченко)

Вы- сота, м	Видовые числа при разных коэффициентах формы q2 по высотам
0,55	0,65	0,75
М±m	процент погреш-ности (Р)	М±m	процент погреш-ности (Р)	М±m	процент погреш-ности (Р)
	0,405±0,0180	±4,4	0,471±0,0042	±0,9	0,550±0,0052	±0,9
	0,396±0,0171	±4,3	0,463±0,0043	±0,9	0,544±0,0058	±1,1
	0,389+0,0166	±4,3	0,457±0,0037	±0,8	0,540±0,0056	±1,0
	0,383±0,0155	±4,0	0,454±0,0040	±0,9	0,537+0,0054	±1,0
	0,379±0,0156	±4,1	0,450±0,0034	±0,8	0,534+0,0052	±1,0
	0,374±0,0137	±3,7	0,447±0,0032	±0,7	0,531+0,0046	±0,9
	0,371±0,0138	±3,7	0,444±0,0023	±0,5	0,529+0,0049	±0,9
	0,367±0,0120	±3,3	0,441±0,0020	±0,5	0,527+0,0050	±0,9
	0,364±0,0108	±3,0	0,439±0,0022	±0,5	0,527+0,0048	±0,9
	0,361±0,0091	±2,5	0,437±0,0027	±0,6	0,525+0,0044	±0,8
	0,35±0,0083	±2,3	0,436±0,0028	±0,6	0,524+0,0044	±0,8
	0,357±0,0079	±2,2	0,434±0,0034	±0,8	0,523+0,0048	±0,9
	0,356±0,0076	±2,1	0,433±0,0036	±0,8	0,522+0.0048	±0,9
	0,352±0,0064	±1,8	0,430±0,0048	±1,1	0,520+0,0052	±1,0

Следовательно, видовое число при этом будет зависеть от Н, а не от изменения q₂ по высотам.

Для каждой породы В. Ф. Багинским получены свои цифровые значения параметров а и b, Для Беларуси они имеют вид:

сосна	F=1,268 / Н+0,4092 (5£ Н £ 35)
ель	F=1,004 / Н+0,4343 (5£ Н £ 35)
береза	F=0,980 / Н+0,3988 (11£ Н £ 34)
осина	F=0,887 / Н+0,4196 (11£ Н £ 34)
черная ольха	F=0,737 / Н+0,4521 (11£ Н £ 34)
дуб	F=0,855 / Н+0,4333 (11£ Н £ 34)

По этим уравнениям вычислены средние видовые числа насаждений названных древесных видов.

Они приведены в справочнике “Нормативные материалы для таксации леса Белорусской ССР, М., 1984. Для примера в таблице приведены величины F для разных пород.

Вычисление видовых чисел проводится в основном по уравнению гиперболы, по зависимости f от H. Для молодняков учитывается значение не только Н, но и Д. По формуле v = Σg×Hf и используя значения видовой высоты по приведенным регрессионным уравнениям вычисляют объем как отдельного дерева, так и насаждения в целом.

Средние видовые числа древостоев Беларуси

Средняя	Видовые числа для пород
высота, м	сосна	ель	дуб	береза	осина	ольха черная
	0,643	0,652	0,621	0,609	0,617	0,618
	0,529	0,541	0,517	0,502	0,516	0,525
	0,491	0,504	0,483	0,466	0,482	0,493
	0,472	0,485	0,465	0,448	0,466	0,478
	0,460	0,474	0,455	0,437	0,456	0,468
	0,453	0,467	0,448	0,430	0,449	0,462
	0,447	0,461	0,443	0,425	0,444	9,458

Формула Денцина. Многочисленные расчеты таксаторов показывают, что в спелых и приспевающих лесах наиболее часто встречаются деревья с Н = 25 м и f = 0,5. Если в уравнении для определения объема растущего дерева v = gHf = 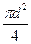Hf допустить, что произведение Hf = 40 / p = 12,74, то формула примет вид v = 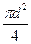× 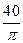=10d². Так как диаметры измеряются в сантиметрах, т.е. в 0,01 м, то d²=0,0001 м и объем ствола выразится

v = 10d² × 0,0001 = 0,001 d 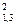, т.е. нужно измерить диаметр на высоте 1,3 м в сантиметрах, возвести его в квадрат и в произведении отделить справа налево три десятичных знака; в результате получаем объем ствола в кубических метрах.

По исследованиям Денцина, предложившего эту формулу, она верна в отношении стволов сосны, имеющих высоту 30 м, а для ели и дуба 26 м. На каждый лишний или недостающий метр высоты ствола надо вносить поправку в полученный по формуле объем: для сосны ±3%; ели ±3-4% и дуба ±5%. Приведенная формула не дает высокой точности и может быть использована лишь для суждения о приближенной величине объема ствола.

Формула Н.Н. Дементьева помимо d_1,3, включает и высоту ствола. Установив, что при q₂ = 0,65 видовое число f может быть принято равным 0,425, он включил эту величину в общую формулу объема растущего ствола: v=gHf= 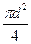Н ^. 0,425=(3,14 ^. 0,425 d²H) / 4 = 0,333 d²H= d^{2 .} H/3

Для стволов, имеющих иные q₂, в формулу к высоте ствола вносится поправка и формула приобретает вид v = d^{2 .} (H+h) / 3 На каждые 0,05q₂ следует прибавлять или убавлять 3 м. Так, для стволов, у которых q₂ = 0,70, поправка +3 м; при q₂ = 0,75 поправка +6 м; при q₂ = 0,60 поправка со знаком минус, т.е. - 3 м и т.д. Сопоставление объемов, полученных по формуле (6.25), с данными объемных таблиц показало, что значения объемов близко совпадают.

Формула проф. Б.А. Шустова выводится из соотношения q₂ : f, которое, по данным его исследований, носит константный характер: для сосны q₂ : f = 1,468, для дуба q₂ : f = 1,476, для ели q₂ : f = 1,450.

Исходя из этих соотношений получена формула объема по трем измерениям: v = 0,534 d_1/2 d_1/3 H

Например, d_1,3 = 20 см; d_1/2 = 14 см; Н = 23 м; тогда

v = 0,534 ^. 0,20 ^. 0,14 ^. 23 = 0,342 м³.

По таблицам Союзлеспрома объем такого ствола v = 0,332 м².

Таблицы объема и сбега древесных стволов. Используя обмеры ствола через 1; 2 м или через 0,1Н, а также имея коэффициенты формы, для облегчения таксационных расчетов моделируют сбег ствола и составляют по ним таблицы сбега. Для этого замеряют большое количество деревьев (несколько сот или тысяч деревьев одной породы), группируют их по диаметрам и высотам и усредняют значения диаметров на разной высоте. По полученным величинам строится адекватная аналитическая модель. Таблицы сбега обычно объединяют с таблицами объемов. Они имеют следующий вид.

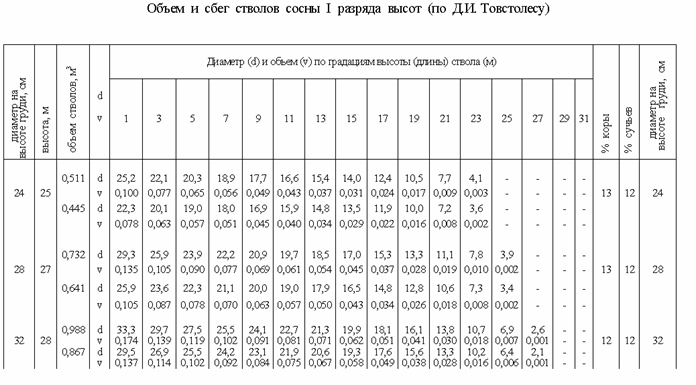
В настоящее время в практике лесного хозяйства применяют разные массовые таблицы.

Исходя из сочетания основных сомножителей объема ствола (d_1,3,H,f) существующие массовые таблицы объемов древесных стволов могут быть подразделены на следующие виды.

Массовые таблицы типа баварских. Объем ствола v приводится на основании измерений диаметра на высоте 1,3 м и высоты Н для некоторой средней формы ствола, представленной в таблицах. Для отдельных видов таблиц этого типа дополнительно учитываются элементы лесобиологического порядка: возрастные группы, области роста, вариации формы стволов и др.

К этому типу относятся следующие таблицы:

1) баварские; 2) общегерманские; 3) удельные таблицы Крюденера; 4) ряд таблиц других отечественных авторов.

В таблицах данного типа для одинаковых ступеней толщины предусмотрено значительное число высот, а следовательно, такое же количество отдельных объемов стволов.

Массовые таблицы по разрядам высот. Объемы стволов приводятся на основе: 1) измерения диаметров стволов на высоте 1,3 м; 2) отнесения таксируемой совокупности деревьев к одному из разрядов высот, представленных в таблицах, при заранее установленных соотношениях между диаметрами и высотами и 3) некоторой средней формы стволов, принятой в таблицах.

Таким образом, для таксируемой совокупности деревьев высота для каждой ступени толщины непосредственно не устанавливается, а весь объект таксации относится к одному из разрядов высот, имеющихся в таблицах.

В таблицах по разрядам высот соотношения между d и Ноформляются в виде соответствующих кривых высот по числу их разрядов. Для каждой ступени толщины приводится столько объемов, сколько разрядов высот представлено в таблицах. В свою очередь число разрядов высот различно в разных таблицах и обычно включает 3, 4, 5 и более разрядов.

К этому типу таблиц относятся следующие: 1) русские временные массовые таблицы (1886 г.); 2) современные таблицы по разрядам, называвшиеся ранее таблицами объемов по бонитетам, и 3) ряд таблиц зарубежных стран.

Таблицы объемов стволов по коэффициентам формы q₂. В таблицах этого типа объемы стволов даются на основе трех измерений для каждого ствола, а именно: 1) диаметра на высоте 1,3 м (d_1,3); 2) высоты ствола Н и 3) второго коэффициента формы q2=d_1/2 : d_1/3.

К таким таблицам относятся: 1) таблицы Шиффеля для сосны, ели, пихты, лиственницы; 2) таблицы Мааса для сосны и ели и 3) таблицы Ионсона для сосны и ели.

Из приведенной структуры трех типов таблиц видно, что число признаков, по которым учетные единицы объединяются в совокупности, называемые входами таблиц, различно. В таблицах первого типа входами являются порода, диаметр на высоте 1,3 м и высота ствола, в таблицах второго типа — порода, диаметр и разряд высот и, наконец, в третьем типе — диаметр на высоте 1,3 м; высота Н и коэффициент формы q₂. Что касается древесной породы, то она может быть опущена. Так, таблицы Мааса и Ионсона составлены для хвойных пород Швеции без подразделения на породы, что отвечает выводам ранее рассмотренных соотношений между видовыми числами, высотами и коэффициентами формы q₂.

Массовые таблицы типа баварских. Баварские массовые таблицы появились в 1846 г. и были первыми по времени их составления. Исходным материалом послужили данные обмера в лесах Баварии свыше 40 тысяч стволов разных пород. Собранный материал был подвергнут статистической обработке с вычислением средних величин и последующим их графическим сглаживанием.

Группировка опытных материалов в процессе их обработки проводилась по породам, d_1,3, Н и возрастным категориям: средневозрастные до 60 лет, приспевающие 61-90 лет и спелые свыше 90 лет. Первоначально были разработаны таблицы средних видовых чисел по указанной группировке, при помощи которых объемы стволов вычислялись по формуле v = gHf. .

Измерив d_1,3 и Н, искомый объем ствола легко найти в соответствующей таблице на пересечении граф диаметра и высоты. Количество высот, а следовательно, и объемов стволов для отдельных диаметров составляет 30, что дает широкие возможности подбора объемов по d и Н.

Баварские таблицы долгое время были единственными, они нашли практическое применение и за пределами Баварии, например в царской России.

При таксации совокупности деревьев на площади однородных участков леса нет необходимости измерять высоту каждого дерева. Учитывая закономерное соотношение в этом случае между d и Н, на основе замеров высот по ступеням толщины строят кривую высот, сглаженную надлежащим образом, по которой и берутся высоты по ступеням толщины, что предельно упрощает применение таблиц этого типа. Использовав данные перечета деревьев по породам и ступеням толщины и построив такую кривую высот, вычисляют запас данной совокупности по следующей форме:

Ступени толщины, см	Высоты, м	Число стволов, шт.	Объем одного ствола, м3	Объем всех стволов, м3

Массовые таблицы типа баварских находят применение для таксации совокупности отдельных деревьев (понятие, введенное проф. Н.В. Третьяковым), обладающих каким-либо однородным качественным признаком, например отобранные и заклейменные стволы сосны для заготовки авиасортиментов, стволы березы, дающие фанерные кряжи и т. п. Такие деревья, как правило, выборочно отбираются на значительной площади, они территориально разъединены, зачастую произрастают в разнообразных условиях внутренней и внешней среды. В процессе роста такие деревья не влияли друг на друга, поэтому не наблюдалось закономерных соотношений между d и Н, характерных для совокупности деревьев, растущих в составе насаждений. В этом случае перечет деревьев следует проводить не только по ступеням толщины, но и по классам высот 2-3 м.

Общегерманские массовые таблицы опубликованы в 1876 г. По методам построения и результатам применения они близки к баварским таблицам. Материалом для построения таблиц послужили обмеры более 60 тысяч древесных стволов в разных областях Германии.

Для стволов средней формы объемы даны в двух вариантах:

объем всего ствола (Baumholz) и объем крупной древесины (Derbholz), включающей объем ствола толщиной до 7 см в вершине. По разности этих объемов можно определить кубатуру сучьев и мелкой древесины.

Для стволов дуба в таблицах приводятся объемы средней формы при q₂=0,70; при таксации сбежистых (q₂=0,60) и полнодревесных (q₂=0,80) стволов нужно увеличивать или уменьшать средние объемы на 6-8%.

Объемы стволов по германским таблицам в сопоставлении с баварскими дают некоторое преувеличение (от 2 до 8%); это объясняется тем, что модельные деревья, использованные для составления таблиц, отбирались в качестве средних моделей и оказались лучшей формы, чем использованные для составления баварских, взятых в порядке сплошных рубок.

Порядок пользования германскими таблицами аналогичен описанному для таблиц баварских.

Общегерманские таблицы предусматривали две области роста: северную и южную Германию, а также возрастные группы деревьев: до 40 лет, 41-80 и выше 80 лет.

Удельные массовые таблицы А. Крюденера были составлены в период 1908-1913 гг. в России удельным лесничим А. Крюденером на основании большого фактического материала, собранного в лесах бывшего Удельного ведомства. При этом было обмерено свыше 108 тысяч модельных деревьев разных пород.

Методика составления этих таблиц предусматривала влияние на объем и сбег стволов (помимо обычных таксационных признаков) естественноисторических факторов: области роста; условий местопроизрастания, характеризуемых типами леса; возрастных категорий и типов деревьев по форме.

Предусматривалось две области роста — северная и южная Россия, — причем границы между ними были указаны довольно схематично.

Типы леса, дающие близкие по таксационным признакам объемы и сбег стволов, объединялись в группы. Для сосны было выделено пять групп, для ели и березы — четыре, для остальных пород этот признак не учитывался. По утверждению проф. М.М. Орлова, деление на группы типов леса приближается к классификации по бонитетам.

Для сосны также предусматривались три возрастные категории: от 65 до 90, от 95 до 120 и от 125 до 150 лет.

В целях индивидуализации формы стволов в таблицах А. Крюденера были приняты следующие типы деревьев:

1) деревья полнодревесные, выросшие в сомкнутых насаждениях;

2) деревья средней полнодревесности;

3) сильно сбежистые, выросшие в изреженных насаждениях.

Необходимо отметить, что приведенная группировка материалов не была выдержана для всех пород. По мере накопления и обработки этих материалов было установлено ничтожное влияние отдельных признаков, и автор пошел по линии упрощения структуры таблиц; в частности, для стволов липы даются объемы по диаметру и высоте с учетом лишь двух форм стволов.

Особенностью этих таблиц является наличие данных по сбегу стволов по секциям 1,4 м, а также толщины коры на разных высотах. Все измерения приведены в старых русских мерах: аршинах, вершках, футах. А. Крюденер рекомендовал для таксируемого участка строить кривую соотношений d и Н.

Весь материал опубликован в 20 томах. Порядок пользования таблицами такой же, как и баварскими. Таблицы А. Крюденера, составленные в русских мерах, не могли получить широкого производственного использования, особенно с введением метрической системы измерения в лесном хозяйстве.

Таблицы имеют ряд недостатков:не использованы известные к тому времени более совершенные способы обработки экспериментальных данных; форма древесных стволов была установливалась по фотографиям, а не путем объективных критериев, обоснованных измерениями диаметров и высот; использование возрастных категорий, не является достаточно обоснованным

На основе материалов своих таблиц А. Крюденер составил таблицы объемов бревен различных пород, причем таблицы объемов еловых бревен, составленные на основе обмера 26 тысяч бревен, в настоящее время, будучи перечислены на метрические меры, утверждены в качестве ГОСТ 2708, которые после небольших уточнений применяются как ГОСТ 2708-75.

Массовые таблицы по разрядам высот. Таблицы типа баварских получили исключительное применение в лесном хозяйстве западноевропейских стран. Огромные масштабы русского дореволюционного, а также современного лесного хозяйства требовали упрощения техники таксации леса на корню и вместе с тем обеспечения необходимой ее точности.

Ввиду этого в условиях Восточной Европы широкое применение получили объемные таблицы по разрядам высот (рисунок).

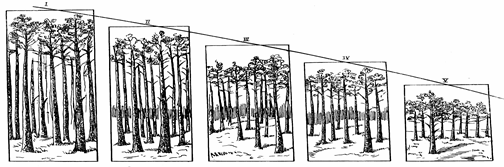Схема распределения насаждений по разрядам высот

Первыми таблицами этого типа были опубликованные в 1886 г. “Русские временные массовые таблицы”, которые использовались на протяжении сорокалетнего периода и были отменены только в 1928 г.

Для стволов дуба было принято четыре разряда высот, а для остальных пород — по три разряда. Объемы давались для средней формы.

Таблицы объема дополнены данными сбега стволов, на основе чего были составлены простейшие сортиментные таблицы, позволяющие проводить материальную и денежную оценку леса на корню с использованием таксовых цен.

Способ применения таблиц несложен. Для каждой пароды на таксируемом участке путем замеров ряда высот главнейших ступеней толщины определяли разряд высот, после чего для каждой ст