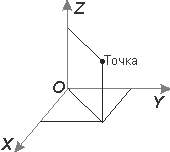
Пространственная прямоугольная система координат
Начало пространственных прямоугольных координат либо определяется под условием совмещения с центром масс Земли (в общеземных системах), либо находится вблизи от него (в референцных системах).
Ориентировка оси Z в каждой системе координат выполняется с учетом ориентировки средней оси вращения Земли. При установлении системы среднего полюса, в том числе и полюса в Системе МУН, не накладывают условия прохождения средней оси вращения через центр масс Земли, поэтому и в референцных и в общеземных системах оси Z не совпадают со средней осью вращения, а параллельны ей.
Плоскость XOY перпендикулярна оси Z и средней оси вращения Земли. Плоскость XOZ выбирается под условием ее параллельности плоскости начального астрономического меридиана. Благодаря названным условиям устанавливается взаимная связь между земными и звездными системами координат, применяемыми в геодезии. Оси Z не совпадают и не параллельны оси Мира, поэтому в установлении этой связи участвуют координаты мгновенного полюса относительно среднего полюса. Ось Z пересекает поверхность Земли в двух точках, которые являются геодезическими полюсами. Плоскость XOZ пересекает поверхность Земли по линии, называемой начальным геодезическим меридианом, а плоскость XOY — по линии, которая является геодезическим экватором.
Начала разных систем координат по-разному расположены относительно Земли, т. е. относительно ее центра масс, поэтому в разных системах координат геодезические полюсы, начальные геодезические меридианы и экваторы на земной поверхности разные. В общеземных системах эта разница невелика и вызвана тем, что совмещение начал этих систем с центром масс Земли и ориентирование осей выполняется не безошибочно.
Положение любой точки задается тремя пространственными координатами — абсциссой X, ординатой У, аппликатой Z.
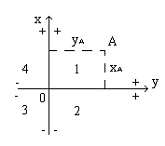
Прямоугольная система координат
Прямоугольная система координат – система плоских координат образованная двумя взаимноперпендикулярными прямыми линиями, называемыми осями координат x и y. Точка их пересечения называется началом или нулем системы координат. Ось абсцисс – OX, ось ординат – OY.
Существуют две системы прямоугольных координат: левая и правая. В геодезии чаще применяется левая система. Положение точки в прямоугольной системе однозначно определяется двумя координатами X и Y; координата X выражает расстояние точки от оси ОY, координата Y – расстояние от оси OY.
Значения координат бывают положительные (со знаком "+") и отрицательные (со знаком "-") в зависимости от того, в какой четверти находится искомая точка.
1.2. Система пространственных прямоугольных координат, система геодезических координат, система плоских прямоугольных геодезических координат, местные системы координат.
1.3. Система геодезических параметров Земли (ПЗ-90) и Мировая геодезическая система координат (WGS-84).
Тоже самое что и в 1.15 как я понял
1.4. Исходная геодезическая основа.
Местная система координат.
Под местной системой координат понимается условная система координат, устанавливаемая в отношении ограниченной территории, не превышающей территорию субъекта Российской Федерации, начало отсчета координат и ориентировка осей координат которой смещены по отношению к началу отсчета координат и ориентировке осей координат единой государственной системы координат, используемой при осуществлении геодезических и картографических работ.
Система координат – это способ задания положения точек в пространстве. Главное свойство всех систем координат – положение любой точки однозначно определяется ее координатами.
Местные системы координат устанавливаются для проведения геодезических и топографических работ при инженерных изысканиях, строительстве и эксплуатации зданий и сооружений, межевании земель, ведении кадастров и осуществлении иных специальных работ.
Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).
Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами.
Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.
Постановление Правительства РФ от 03.03.2007 N 139 «Об утверждении Правил установления местных систем координат»
Для установления местных систем координат городов, осевой меридиан системы проходит через центр города. Поправки за переход на плоскость проекции Гаусса-Крюгера уменьшаются. В Москве при работе с государственной СК поправки за переход составляют величину 1:3500, а если использовать местную СК то 1:35000. В Москве используют эллипсоид Бесселя.
В целях ведения ГКН, составления землеустроительных карт (планов), определения координат границ земельных участков и др. на территории РФ применяют местные системы координат.
Местную систему координат задают в пределах территории кадастрового округа. Местная система плоских прямоугольных координат является системой плоских прямоугольных геодезических координат с местными координатными сетками проекции Гаусса
При разработке местных систем координат используют параметры эллипсоида Красовского.
В местных системах координат применяют Балтийскую систему высот. Редуцирование линейных измерений в проекцию Гаусса с местной координатной сеткой и вычисление геодезических вы сот выполняют с помощью «Карты высот квазигеоида над эллип соидом Красовского». Эта карта соответствует государственной рефератной системе.
За основу местных систем координат может быть принята система координат
СК-63, которая покрывает территорию большинства субъектов Российской Федерации несколькими самостоятельными блоками. В то же время, вместо блочного покрытия территории страны, местные системы координат можно устанавливать на территории кадастрового округа или кадастрового района.
Применение единой местной системы координат позволяет однозначно и без дополнительных преобразований вести Единый государственный реестр земель.
Местные системы координат имеют названия. Названием системы может являться ее номер, равный, например, коду (номеру) субъекта РФ или города, устанавливаемому в соответствии с .«Общероссийским классификатором объектов административно-территориального деления».
В каждой местной системе координат устанавливаются следующие параметры координатной сетки проекции Гаусса:
· долгота осевого меридиана первой зоны L0
· число координатных зон N;
· координаты условного начала X0, Y0;
· угол поворота θ осей координат местной системы относительно государственной в точке местного начала координат;
· масштаб местной системы координат относительно плоской прямоугольной системы геодезических координат СК-42 или СК-95;
· высота H0 поверхности (плоскости) принятой за исходную, к которой приведены измерения и координаты в местной системе;
· референц-эллипсоид, к которому отнесены измерения в местной системе координат;
· соответствующие формулы преобразования плоских прямоугольных геодезических координат.
Преобразование координат из одной плоской системы координат
в другую.
При преобразовании координат из одной системы в другую используют различные алгоритмы. Участвующие в преобразовании геодезические пункты должны принадлежать одной и той же координатной зоне местной системы координат. Рассмотрим порядок преобразования координат по двум связующим точкам.
Дано: координаты п точек (пунктов) в системе координат первого блока (старая система координат) – x1y1, x2y2,…, xnyn; координаты тех же точек в системе координат второго блока (новая система координат) — x1´y1´, x2´y2´,…, xn´yn´
Примем, что точки с номерами 1 и 2 являются связующими, т. е. для них известны плоские прямоугольные координаты как в старой, так и новой системах координат.
Требуется определить координаты оставшихся (n2) точек в новой системе координат— x3´y3´, …,xn´yn´
Порядок решения задачи.
1. Вычисляют угол разворота (поворота) θ между новой и старой системами плоских прямоугольных координат.
2. Решают две обратные геодезические задачи: для отрезка, координаты начальной 1 и конечной 2 точек которого заданы в старой системе координат; для этого же отрезка, но в новой системе координат.
В результате решения этих задач получают соответствующие дирекционные углы α и горизонтальные приложения S, а именно:
в старой системе координат — α1 и S1, а в новой - α2 и S2.Угол разворота θ вычисляют по формуле θ =α2-α1.
3.Находят масштабный множитель m= S2/S1
а также коэффициенты К1= mcos θ, К2= msin θ
4. Вычисляют преобразованные координаты x´,y´ соответствующих точек, используя полученные коэффициенты К1 и К2 путем последовательного перехода от пункта к пункту по формулам:
X´j= X´j-1 + (Xj - Xj-1 )*К1- (Yj - Yj-1)*К2
Y´j= Y´j-1 + (Yj - Yj-1 )*К1- (Xj - Xj-1)*К2
Где j = 2,3,…, n.
При j =1 X´(j=1)= X1 и Y ´(j=1)= Y 1 .
В данной задаче первой (j -1 = 1) является начальная точка отрезка, а последней — конечная точка этого же отрезка (j= n, X´(j=n) = Xn и
Y ´(j= n)= Yn) .
Вычисление преобразованных координат второй связующей
точки (j= n) — контроль соответствующих вычислений.
При наличии более чем двух связующих пунктов параметры преобразования вычисляют, как правило, с использованием метода наименьших квадратов при условии: сумма квадратов поправок к координатам связующих пунктов в двух системах координат должна быть минимальной.
Переход от системы координат с одним осевым меридианом, к системе координат с другим осевым меридианом (из одной зоны в другую), в геодезии получил название «перехода из зоны в зону».
Рассмотрим в общем виде такое преобразование плоских прямоугольных координат Гаусса – Крюгера.
Все системы плоских прямоугольных координат (различных зон), вероятно, могут быть связаны между собой через систему геодезических координат, так как геодезические координаты B и L, являясь едиными для всей поверхности эллипсоида, не связаны с осевыми меридианами зон. Поэтому, наиболее общим, естественным и простым здесь будет путь, основанный на двойном преобразовании координат сначала плоских прямоугольных координат в геодезические, а затем геодезических – в плоские прямоугольные координаты, соответственно, по формулам (3.64) и (3.58). Если обозначить координаты условной исходной зоны через ха, уа, а координаты в определяемой зоне – через хб, уб, то более детально это можно показать схематично следующим образом
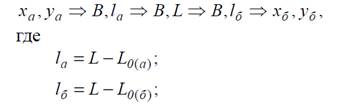
где L0(a) и L0(б) – долготы осевых меридианов, соответственно, зоны а и зоны б, а знак⇒ заменяет слова «преобразуется в…»
Этот способ в геодезической литературе получил название аналитического и имеет точность, соответствующую точности формул, применяемых для преобразования координат.