Ориентирование линий. Азимут, румб и дирекционный угол

Азимут - угол между горизонтальной плоскостью меридиана и вертикальной плоскостью наблюдаемого объекта (служит для определения местоположения светил, летательных аппаратов и др.).

При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.

Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.

В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута. Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).

Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.

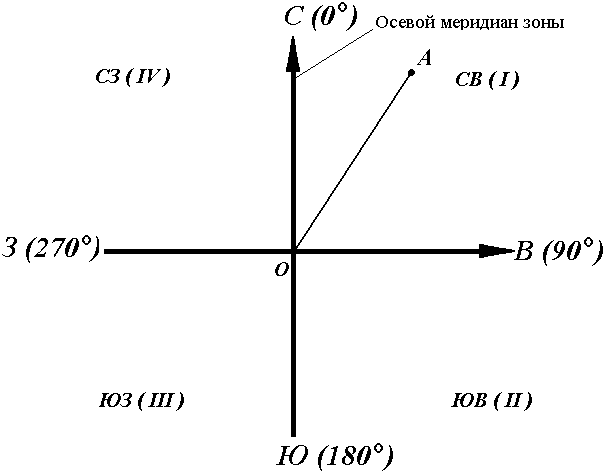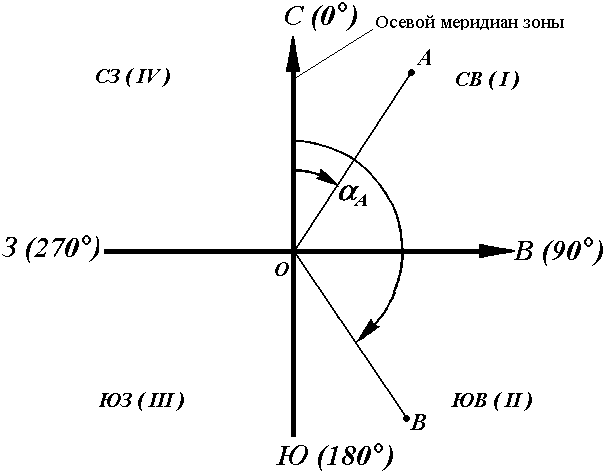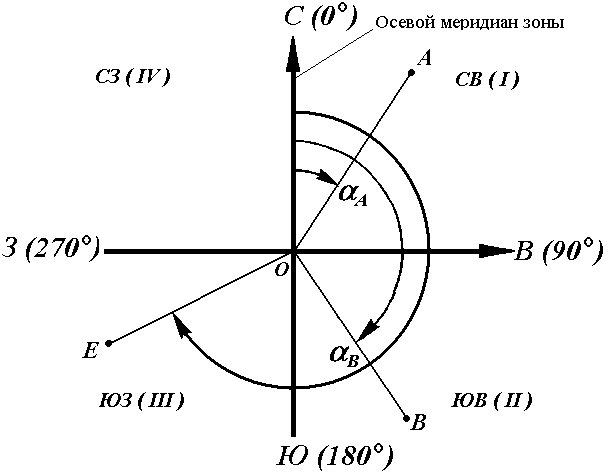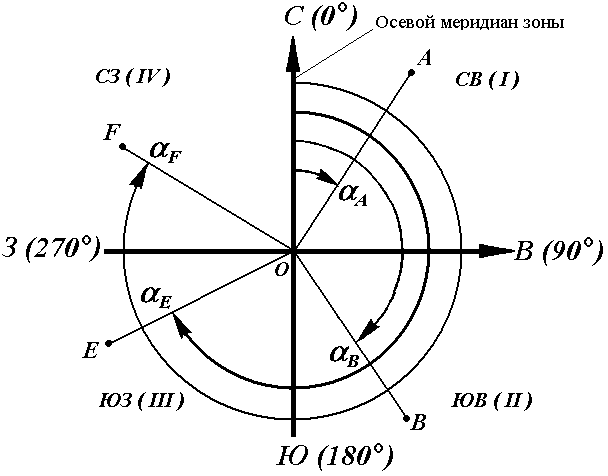
Рис. 16. Дирекционные углы

Для линии ОА её дирекционным углом в точке О является горизонтальный угол α_ОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – α_ОВ , α_ОE , α_ОF.

Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.

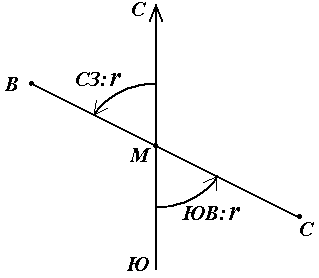
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим α_BC является прямым дирекционным углом линии ВС в точке М, а угол α_CB – обратным дирекционным углом этой же линии в той же точке.

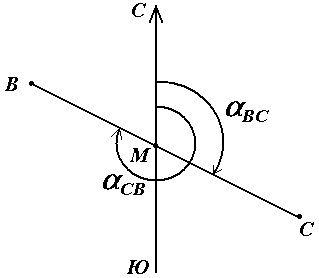
Рис. 17. Прямое и обратное направление линии

Из рисунка видно, что α_CB = α_BC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.

Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).

Осевым румбомназывается острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.

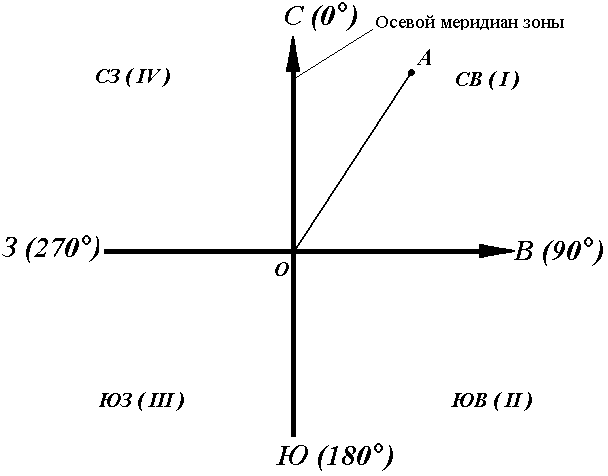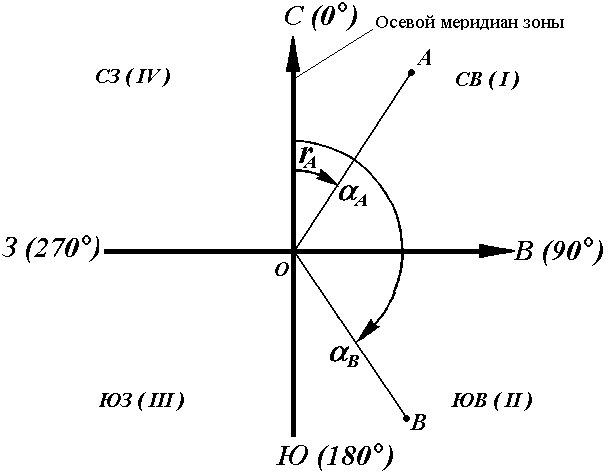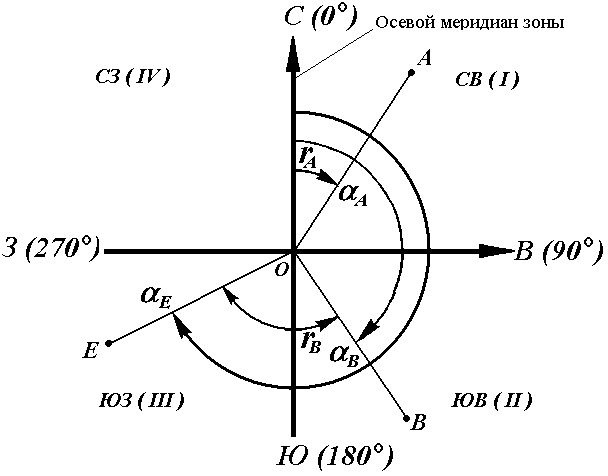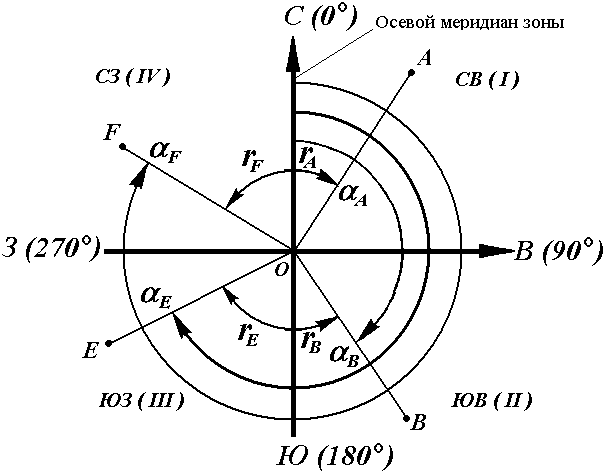
Рис. 18. Румбы и дирекционные углы

Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).

Зависимость между дирекционными углами и румбамиопределяется для четвертей по следующим формулам:

I четверть (СВ) r = α

II четверть (ЮВ) r = 180° – α

III четверть (ЮЗ) r = α – 180°

IV четверть (СЗ) r = 360° – α

Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.

Горизонтальное проложение

Горизонтальное проложение - проекция участка земной поверхности на поверхность земного эллипсоида с помощью нормалей (прямых, перпендикулярных к эллипсоиду).

Измеряемые на местности линии чаще всего бывают наклонными к горизонтальной плоскости. Для составления же плана нужно знать их горизонтальные проложения(проекции). Так, вместо измерений наклонной линии D (рисунок 20) нужно определить длину горизонтального проложения d.

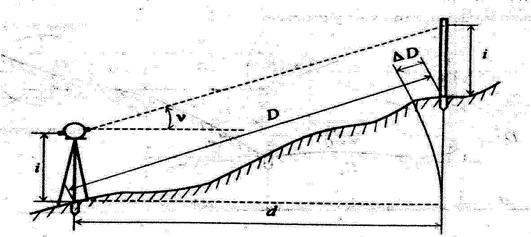
Рисунок. Приведение наклонной линии к горизонту

Для того чтобы получить горизонтальное проложение, то есть проекцию линии на горизонтальную плоскость, необходимо измерить угол наклона линии n по вертикальному кругу теодолита или эклиметром. Величина d горизонтальной проекции Dнайдется по формуле:

d = D × cosn(11)

Практически поправку за приведение линии к горизонту DD или проще поправку за наклон вычисляют по формуле:

DD = D – d = D – d × cos n = D ( 1 - cosn ) = 2×D×sin² n/2.

Поправку за наклон DD всегда вычитают из измеренной наклонной линии, т.е.: d = D - DD.