УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
Дисциплины PUNP «Применение удобрения нового поколения»
Специальность: –6М080900 «Плодоовощеводство»
2 кредита
Алматы 2017г
Учебно-методический комплекс по дисциплине «Применение удобрения нового поколения» для студентов КазИТУ по специальности : 6М080900 «Плодоовощеводство».
Составитель: д.т.н. профессор Султанова Зиада Клычбаевна Алматы: КазИТУ, 2017 г.
Аннотация: Учебно-методический комплекс дисциплин студента (УМК ДС) представляет собой документ, определяющий концепцию конкретного курса. Учебно-методический комплекс составляется тьютором на основе типовой программы, издается типографским способом и предназначается для студентов, обучающихся по кредитной системе. Учебно-методический комплекс выдается студенту перед началом изучения дисциплины и содержит учебную программу дисциплины (Syllabus), тематический план курса, систему заданий для самостоятельной работы студентов, график выполнения отчетных работ по дисциплине, тестовые задания для самоконтроля, тематику письменных работ и перечень экзаменационных вопросов. Ценность данного УМК состоит в распределении учебного времени по темам и видам учебных занятий, организации самостоятельной работы студентов в аудиторное и внеаудиторное время, активизации познавательной и творческой деятельности студентов и обеспечения взаимосвязи учебного и исследовательского процессов.
УМКД обсужден на заседании кафедры
протокол № 1 от 23.08. 2016 г. _____________
УМКД утвержден на заседании учебно - методического совета Каз.ИТУ
протокол № 1 от 24.08.2016
© Казахстанский инженерно-технологический университет, 2017 г.
Министерство образования и науки Республики Казахстан
Типовая программа
PUNP «Применение удобрения нового поколения»
М080900 – «ПЛОДООВОЩЕВОДСТВО»
2 кредита
Алматы 2017 г
Пояснительная записка
ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
Цель преподавания дисциплины: изучение физических и физико-химических, водно-воздушных и тепловых режимов, а также их агрохимические свойства и генезис основных типов почв РК и СНГ.
Задачи изучения дисциплины:
- составлять и осуществлять на практике систему агротехнических и специальных мероприятий для повышения плодородия почв и урожайности возделываемых сельскохозяйственных культур;
- подготовки и проведения экспертных работ по оценке почвенного покрова для обоснования организации и развития отраслей народного хозяйства;
- проведение земельно-кадастровых работ и экономической оценке земель;
- составление почвенных карт и картограмм хозяйствующим субъектам;
- определить степень соответствия почвенных условий к требованиям для тех или иных сельскохозяйственных культур;
- применять методы исследования почв в полевых и лабораторных условиях.
Пререквизиты дисциплины
Для изучения курса «Почвоведение» студентам необходимы знания следующих дисциплин:
- Растениеводство
- Микробиология
- Земледелие
Постреквизиты дисциплины
Знания данного курса необходимы при изучении дисциплин:
- Землеустройство
- Агрохимия
- Система применения удобрений
ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ
| Введение | |
| Комбинаторика конечных множеств. | |
| Реккурентные соотношения. Производящие функции. | |
| Элементы теории графов. | |
| Алгоритмы теории чисел. | |
| Конечные поля. | |
| Стандартные задачи криптографии. | |
| Введение в теорию кодирования. | |
| Алгебра логики. | |
| Элементы математической логики. |
СОДЕРЖАНИЕ
Введение
Дисциплина «Дискретная математика» ставит своей главной целью – ознакомление с базовыми алгоритмами дискретной математики и овладение основными результатами этой дисциплины для создания программных продуктов и моделирование реальных процессов.
Задачей этого курса является не только сообщение известного запаса сведений (определений, теорем, их доказательств, связей между ними, методов решения задач) и обучение их применениям. В его задачу входят развитие у учащихся логического мышления и математической культуры, необходимых для изучения математики (да и вообще для проведения научно-исследовательской работы), развитие математической (качественной, аналитической и геометрической) интуиции.
Элементы теории графов.
Понятие графа. Графы, сети, коды. Виды графов. Представление графов. Эйлеровы и гамильтоновы графы. Деревья. Хроматическое число графов. Теорема Эйлера о планарных графах. Теорема Понтрягина-Куратовского.
Алгоритмы теории чисел.
Кольцо целых чисел. Теорема о делении с остатком. Алгоритм Эвклида. Простые и составные числа. Основная теорема арифметики. Взаимно простые числа и их свойства. Теоремы Ферма и Эйлера. Китайская теорема об остатках.
Конечные поля.
Сравнения и их свойства. Кольцо вычетов. Необходимое и достаточное условие, что кольцо вычетов является полем. Построение конечных полей. Алгоритм нахождения примитивного элемента поля.
Алгебра логики.
Булевы алгебры. Булевы функции. Лемма о числе булевых функции. Равносильные преобразование булевых функции. СДНФ и СКНФ. Полиномы Жегалкина. Теорема Жегалкина. Основные классы булевых функции. Полные системы логических связок.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ СЕМИНАРСКИХ ЗАНЯТИЙ
1. Множества и операции над ними.
2. Принципы суммы и произведения.
3. Принцип включения и исключения. Характеристическая функция подмножества.
4. Принцип Дирихле и его применения.
5. Бинарные отношения и операции над ними.
6. Бином Ньютона. Свойства биномиальных коэффициенттов.
7. Рекурентные соотношения. Числа Фибоначчи и Каталана.
8. Элементарные производящие функции и определямые ими ряды.
9. Произведение производящих функции. Операция свертки.
10. Представление графов. Эйлеровы и гамильтоновы графы. Деревья.
11. Хроматическое число графов. Применения теоремы Эйлера о планарном графе.
12. Кольцо целых чисел. Кольцо вычетов. Сравнения.
13. Малая теорема Ферма. Теорема Эйлера.
14. Китайская теорема об остатках.
15. Построение полиномов Жегалкина.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬОЙ РАБОТЫ СТУДЕНТОВ
1. Теорема Эрдеша-Шекереша.
2. Нахождение производящей функции для ряда Фибоначчи.
3. Нахождение производящей функции для ряда Каталана.
4. Делители нуля, нильпотентные и обратимые элементы в кольце вычетов. Идеалы и гомомрфизмы.
5. Решение систем сравнении первой степени.
6. Построение полей Галуа. Вычисления в полях Галуа.
7. Примеры задач криптографии с открытым ключом.
8. Примеры задач теории кодирования.
9. Линейно реккурентные соотношения.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ С ПРЕПОДАВАТЕЛЕМ
1. Применения теоремы о разбиении.
2. Перестановки, размещения и сочетани.
3. ТеоремаЛагранжа для конечных групп.
4. Классические алгебраические системы.
5. Конечные группы.
6. Построение конечных полей.
7. Вычисления на конечных полях.
8. Подполя поля Галуа.
9. Алгоритмы нахождения примитивного элемента конечного поля.
Министерство образования и науки Республики Казахстан
Казахстанский инженерно-технологический университет
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
PUNP «Применение удобрения нового поколения»
для специальности магистратуры 6М080900 – «Плодоовощеводство»
Форма обучения - дневная
Количество кредита – 2
Курс - 1
Семестр - 2
Лекции - 15 часов
Практические занятия -15часов
СРСП - 30 часов
СРС - 30 часов
Вид контроля: Экзамен
Всего:90 часов
Алматы 2016
Рабочая учебная программа дисциплины (syllabus) составлена по дисциплине «Применение удобрения нового поколения» на основании типовой учебной программы для специальности для специальности магистратуры 6М080900 – Плодоовощеводство
Рассмотрена и одобрена на заседании кафедры «Технологии, оборудования и стандартизации»
«___23__»_августа2016г. Протокол № _1___
Зав. кафедрой ТОиС ______________ Каржаубаев К.Е.
Составитель ______________ Султанова З.К.
Рассмотрена и утверждена на заседании учебно-методического совета протокол № 1 от 24.08.2016
© Казахстанский инженерно-технологический университет, 2016
Тематический план
| Наименование темы | Количество академических часов | |||||
| Лекций | Практические занятия | Лабораторные занятия | СРО(из них) | |||
| СРСП | СРС | |||||
| Множества. Функции и отношения. Тождества алгебры множеств. | ||||||
| Мощность множества. Конечные и бесконечные множества. Отношения. Отношения и основные операции над ними. | ||||||
| Специальные бинарные отношения. Порядковые отношения. | ||||||
| Отношения эквивалентности. Теорема о разделении. Функции. Функции и операции над ними. | ||||||
| Инъекция, сюръекция, биекция. Правила вычисления. Правило Дирихле. | ||||||
| Правило входа и выхода. Замена. Размещение и подбор. Бином Ньютона. Треугольник Паскаля. | ||||||
| Инъекция, сюръекция и биекция в конечных множествах. Метод математической индукции. Рекуррентные отношения. | ||||||
Операция деления на целочисленных кольцах. Простые и сложные числа. Сравние целых чисел по модулю 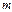 | ||||||
| Китайская теорема об остатках. Мультипликативные функции. | ||||||
| Теоремы Эйлера и Ферма. Последовательные дроби. | ||||||
| Решение уравнении в целых числах. Шифрование. Криптосистема с открытым ключом. | ||||||
| Определение графов. Мультиграф. Изоморфизм графов. | ||||||
| Внутренние графы. Операции применяемые над графами. | ||||||
| Связь графов. Эйлеровые графы. Плоские графы. Ветки и леса. | ||||||
| Машина Тьюринга. Программы копирования и замены. | ||||||
| Всего: | ||||||
Основная
1. Судоплатов С.В., Овчинникова Е.В., Элементы дискретной математики, М, Инфра – М, 2002.
2. Гаврилов Г.П., Сапоженко А.А., Задачи и упражнения по курсу дискретной математики. М, Наука, 1992.
3. Лавров И.А., Максимова Л.Л., Задачи по теории множеств, математической логике и теории алгоритмов, М, Наука, 1984.
4. Емеличев В.А.және басқалар, Лекции по теории графов, М, Наука, 1990.
5. Р.Грэхем, Д.Кнут, О. Паташник, Конкретная математика, М., Мир, 1998 .
6. Джумадильдаев А.С., Элементы дискретной математики, Учебное пособие, часть 1, Университет Сулеймана Демирели, Алматы, 2004.
7. Судоплатов С.В., Овчинникова Е.В., Элементы дискретной математики, М, Инфра – М, 2002.
8. Новиков Ф. А., Дискретная математика для программистов., СПб, Питер, 2001.
9. Э. Мендельсон. Введение в математическую логику. М.: Наука, 1984.
10. Виноградов И.М., Основы теории чисел, М., Наука, 1972.
11. Емеличев В.А.және басқалар, Лекции по теории графов, М, Наука, 1990.
12. Ершов Ю.Л., Палютин Е.А., Математическая логика. М, Наука,1987.
13. Гаврилов Г.П., Сапоженко А.А., Задачи и упражнения по курсу дискретной математики. М, Наука, 1992.
14. Лавров И.А., Максимова Л.Л., Задачи по теории множеств, математической логике и теории алгоритмов, М, Наука, 1984.
Дополнительная
1. С.В. Яблонский, Введение в дискретную математику, М., Наука, 1979 г.
2. Новиков Ф. А., Дискретная математика для программистов., СПб, Питер,
3. О. Оре, Теория графов , М., Наука, 1985 г.
4. М. Холл, Комбинаторика, М., Мир, 1970 г.
5. Горбатов В. А., Фундаментальные основы дискретной математики. М, Физматлит, 2000.
6. Горбатов В. А., Фундаментальные основы дискретной математики. М, Физматлит, 2000.
7. Яблонский С.В., Введение в дискретную математику. М, Наука, 1986.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахстанский инженерно-технологический университет
Кафедра «Вычислительная техника, автоматизация и телекоммуникация»
«Утверждаю»
Проректор поУНиВ работе
_______к.ф.н.Сарсенбекова Г.А.
“ ____” _____________ 2016г

УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ (SYLLABUS)
PUNP «Применение удобрения нового поколения»
для специальности магистратуры 6М080900 – Плодоовощеводство
2 кредита
Форма обучения - дневная
Количество кредита – 2
Курс - 1
Семестр - 2
Лекции - 15 часов
Практические занятия - 15 часов
Лабораторные занятия - 30 часов
СРСП - 30 часов
СРС - 90 часов
Вид контроля: Экзамен
Всего: 150 часов
Алматы 2016
Учебная программа дисциплины (syllabus) составлена по дисциплине «Применение удобрения нового поколения» на основании типовой учебной программыдля специальности магистратуры 6М080900 – Плодоовощеводство
Рассмотрена и одобрена на заседании кафедры «Технологии, оборудования и стандартизации»
«___23__»_августа 2016 г. Протокол № _1___
Зав. кафедрой ТоиС ______________ Каржаубаев К.Е.
Составитель ______________ Султанова З.К.
Рассмотрена и утверждена на заседании учебно-методического совета протокол № 1 от 24.08.2016
© Казахстанский инженерно-технологический университет, 2016
УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИН (SYLLABUS)
1.Данные о преподавателе:
Султанова Зиада Клычбаевна - преподаватель кафедры «Технологии, оборудования и стандартизации»2 корпус, кафедра ТОиС (№ 307 ауд.)
Контакты: 87017264955
2. Название дисциплины–«Применение удобрения нового поколения».
3. Время и место проведения аудиторных занятий курса указано в расписании учебных занятий, график консультаций СРСП размещен на информационной доске университета и кафедры ТОиС (каб. 313)
4. Пререквизиты и постреквизиты учебной дисциплины
Пререквизиты
биология, химия, технология, математика, экономика
Постреквизиты
Применение удобрения нового поколения
5 Характеристика учебной дисциплины
5.1 Краткая информация о дисциплине.
5.4.Содержание дисциплины
5. 4.1 Теоретическая подготовка (30 час.)
Таблица 1
| № п/п | Наименование тем | Кол-во часов |
| Множества. Функции и отношения. Тождества алгебры множеств. | ||
| Мощность множества. Конечные и бесконечные множества. Отношения. Отношения и основные операции над ними. | ||
| Специальные бинарные отношения. Порядковые отношения. | ||
| Отношения эквивалентности. Теорема о разделении. Функции. Функции и операции над ними. | ||
| Инъекция, сюръекция, биекция. Правила вычисления. Правило Дирихле. | ||
| Правило входа и выхода. Замена. Размещение и подбор. Бином Ньютона. Треугольник Паскаля. | ||
| Инъекция, сюръекция и биекция в конечных множествах. Метод математической индукции. Рекуррентные отношения. | ||
Операция деления на целочисленных кольцах. Простые и сложные числа. Сравние целых чисел по модулю 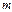 | ||
| Китайская теорема об остатках. Мультипликативные функции. | ||
| Теоремы Эйлера и Ферма. Последовательные дроби. | ||
| Решение уравнении в целых числах. Шифрование. Криптосистема с открытым ключом. | ||
| Определение графов. Мультиграф. Изоморфизм графов. | ||
| Внутренние графы. Операции применяемые над графами. | ||
| Связь графов. Эйлеровые графы. Плоские графы. Ветки и леса. | ||
| Машина Тьюринга. Программы копирования и замены. | ||
| Всего |
5. 4.2 Практическая подготовка
Таблица 2
Тематика практических занятий (15)
| № п/п | Наименование тем | Кол-во часов |
| Тождества алгебры множеств. Множества и основные операции над ними. | ||
| Отношения и основные операции над ними. | ||
| Порядковые отношения. | ||
| Эквивалентные отношения. | ||
| Инъекция, сюръекция и биекция. Правила вычисления. Правило Дирихле. | ||
| Правило входа и выхода. Размещение и подбор. | ||
| Рекуррентные отношения. | ||
| Числа Фиббоначи. Производящие функции. Целые числа и операции деления. | ||
| Мультипликативные функции. | ||
| Последовательные дроби. Приближенные дроби. | ||
| Решение уравнения в целых числах. Нахождение простых чисел в конечных множествах | ||
| Изоморфизм графов. | ||
| Операции применяемые над графами. | ||
| Эйлеровые графы. Плоские графы. Раскраска графов. | ||
| Программы вычисления функций простых чисел. | ||
| Всего |
5.4.3 Наименование тем самостоятельной работы студентов с преподавателем(СРСП),их содержание и объем в часах
Таблица 3
График СРС, СРСП
| недели | Номер занятий по syllabus | СРС | в том числе СРСП | ||||
| Тема и вид задания (с указанием страниц литературы) | Срок выдачи и приема задания (нед) | Тема и вид задания (с указанием страниц литературы) | Срок выдачи и приема задания (нед) | ||||
| 1-3 | СРСП - 1 | Парадокс Рассела (Дж. 3-8 с., Суд. 9-15 с., Мен.) Принцип максимума. Аксиома выбора (Мен.) | Парадокс Рассела (Дж. 3-8 с., Суд. 9-15 с., Мен.) Принцип максимума. Аксиома выбора (Мен.) | ||||
| 3-4 | СРСП - 2 | Обобщенные правила сложения и умножения (Дж. 25-32, Суд. 164-165, Нов. 151-153) | Обобщенные правила сложения и умножения (Дж. 25-32, Суд. 164-165, Нов. 151-153) | ||||
| 4-5 | СРСП - 3 | Повторение, рамещение и подбор. Суд. 157-164, Нов. 135-141 | Повторение, рамещение и подбор. Суд. 157-164, Нов. 135-141 | ||||
| 5-6 | СРСП - 4 | Производящие функции и их свойства. (Дж. 38-45, 53-55, Суд. 22-25, 165-168,86-91, Вин.7-18) | Производящие функции и их свойства. (Дж. 38-45, 53-55, Суд. 22-25, 165-168,86-91, Вин.7-18) | ||||
| 6-7 | СРСП - 5 | Мультипликативность функции Мебиуса. (Дж.58-60,64-67,Вин.54-57,26-32, Суд. 91-98) | Мультипликативность функции Мебиуса. (Дж.58-60,64-67,Вин.54-57,26-32, Суд. 91-98) | ||||
| 7-8 | СРСП - 6 | Мультипликативность функции Эйлера. (Дж. 58-69, Вин. 54-57, 26-32, Суд. 91-98) | Мультипликативность функции Эйлера. (Дж. 58-69, Вин. 54-57, 26-32, Суд. 91-98) | ||||
| 8-9 | СРСП - 7 | Решето Эратосфена. Компьютерное тестирование для определении простых чисел. (Дж. 72-78, Нов. 180-183, 185-188) | Решето Эратосфена. Компьютерное тестирование для определении простых чисел. )Дж. 72-78, Нов. 180-183, 185-188) | ||||
| 9-10 | СРСП - 8 | Описание отношений с помощью графов. (Суд.107-113, Нов.189-197) | Описание отношений с помощью графов. (Суд.107-113, Нов.189-197) | ||||
| 10-11 | СРСП - 9 | Раскраска графов. (Суд. 150-152, 132-135, 114-117, Нов. 197-199, 234-238, Суд. 129-131, 152-154, Нов. 263-264) | Раскраска графов. (Суд. 150-152, 132-135, 114-117, Нов. 197-199, 234-238, Суд. 129-131, 152-154, Нов. 263-264) | ||||
| 11-14 | СРСП - 10 | Задача о мостах Кенисберга | Задача о мостах Кенисберга |
Самостоятельная работа студентов (СРС) и (СРСП) проводится в соответствии с расписанием .
5.5 План изучения дисциплины.
| № п/п | Наименование темы учебной дисциплины | Содержание раздела темы в дидактических единицах |
| Комбинаторика конечных множеств. | Множества и операции над ними. Тождества алгебры множеств. Принципы суммы и произведения. Характеристическая функция подмножества. Принцип включения и исключения. Принцип Дирихле и его применения. Отображения и и виды отображения. Бинарные отношения и операции над ними. Бином Ньютона. Свойства биномиальных коэффициенттов. | |
| Реккурентные соотношения. Производящие функции. | Рекурентные соотношения. Алгебра бесконечных последовательностей. Числа Фибоначчи и Каталана. Теорема Юнга. Числа Белла и Мерсенна. Производящие функции и операции над ними. Элементарные производящие функции и определямые ими ряды. Произведение производящих функции. Операция свертки. | |
| Элементы теории графов. | Понятие графа. Графы, сети, коды. Виды графов. Представление графов. Эйлеровы и гамильтоновы графы. Деревья. Хроматическое число графов. Теорема Эйлера о планарных графах. Теорема Понтрягина-Куратовского. | |
| Алгоритмы теории чисел. | Кольцо целых чисел. Теорема о делении с остатком. Алгоритм Эвклида. Простые и составные числа. Основная теорема арифметики. Взаимно простые числа и их свойства. Теоремы Ферма и Эйлера. Китайская теорема об остатках. | |
| Конечные поля. | Сравнения и их свойства. Кольцо вычетов. Необходимое и достаточное условие, что кольцо вычетов является полем. Построение конечных полей. Алгоритм нахождения примитивного элемента поля. | |
| Стандартные задачи криптографии. | Исторические шифросистемы. Шифры замены и подстановки. Шифросистемы с открытым клюом и алгоритмы дешифрования шифров с открытым ключом. | |
| Введение в теорию кодирования. | Обзор схем кодированя. Неравенство Макмиллана. Алгоритмы сжатия данных, алгоритм Лемпела-Зива. | |
| Алгебра логики. | Булевы алгебры. Булевы функции. Лемма о числе булевых функции. Равносильные преобразование булевых функции. СДНФ и СКНФ. Полиномы Жегалкина. Теорема Жегалкина. Основные классы булевых функции. Полные системы логических связок. | |
| Элементы математической логики. | Высказывания, таблица истинности. формул. Нормальные формы. Понятия предиката и терма. Кванторы и формулы. Понятие модели. Выполнимость формулы в модели. Эквивалентность формул. Универсальные и хорновы формулы. Теорема Эрбрана, сколемизация. Понятие алгоритма. Машины Тъюринга. Методы математических доказательств. |
Политика и процедура курса
Студент обязан:
-во время занятий отключать мобильные телефоны;
-регулярно,без опозданий, посещать все виды аудиторных занятий (лекции, практические занятия, лабораторные занятия) и занятия по самостоятельной работе студента под руководством преподавателя (СРСП);
- самостоятельную работу студента (СРС) выполнять в заданном объёме и установленные сроки с использованием рекомендованной учебной и учебно-методической литературы или других источников в читальных и интернет- залах библиотек;
-строго соблюдать графики сдачи работ(СРСП или СРС)
в заданном объёме(незавершенные работы не засчитываются);
- лично присутствовать на рейтинговых и итоговом контролях;
-регулярно читать периодическую литературу по вопросам организации телекоммуникаций как в РК, так и за рубежом.
Содержание лекционного материала
Лекция 4. Состав почвы
Почва состоит из твердой фазы, жидкой (или почвенного раствора) и газовой фазы (или почвенного воздуха), которые находятся между собой в тесном взаимодействии.
Почвенный воздух отличается от атмосферного повышенным содержанием углекислого газа и несколько меньшим –кислорода. В почве постоянно идет потребление кислорода и выделение СО2 при разложении органического вещества микроорганизмами. В атмосферном воздухе содержится 0,03% СО2, в почвенном растворе 0,3-1%.
Обогащение почвенного раствора углекислым газом усиливает растворяющее действие его на минеральные соединения почвы, способствует переводу их в усвояемые для растений формы. Но избыток СО2 в почвенном воздухе отрицательно влияет на развитие растений.
Жидкая фаза почвы или почвенный раствор- наиболее подвижная и активная часть почвы, в которой соверщаются разнообразные химические процессы и их которой растения непосредственно усваивают питательные вещества.
Состав и концентрация почвенного раствора могут изменяться под влияние разных факторов. Содержание солей в нем повышается при внесении удобрений, снижением влажности почвы, усилении минерализации органического вещества.
Твердая фаза почвы содержит основной запас питательных веществ для растений. Она состоит из минеральной части, на которую приходится 90-98% твердой фазы и органической части, которая играет очень важную роль в ее плодородии. Почти половина твердой фазы почвы приходится на кислород049%, затем идет кремний-33%, более 10% на алюминий и железо, и только 7% на остальные элементы. В состав твердой фазы входит более 45 элементов.
Все элементы твердой фазы почвы содержатся в минеральной части почвы, входят в состав различных минеральных соединений. Углерод, водород, кислород, фосфор и сера находятся и в минеральной , и в органической части почвы. Азот почти полностью содержится в органической части почвы.
Минеральная часть почвы состоит из частиц различных минералов. По химическому составу минералы подразделяются на кремнекислородные соединения или силикаты и алюмокремнекислородные соединения или алюмосиликаты.
Из кремнекислородных соединений наиболее распространен в почве кварц (SiO2), он содержится в виде частиц песка. Почти во всех почвах содержание кварца достигает 60%, а в песках-90%
Алюмокремнекислородные соединения представлены в почве в виде полевых шпатов, слюд, биотита. Разные механические фракции минеральной части почвы различаются между собой по размеру частиц, а также по минералогическому и химическому составу.
Важнейшей частью почвы является органическое вещество почвы. Органическая часть почвы представляет собой сложный комплекс разнообразных органических веществ, которые подразделяются на две группы:
1.Негумифицированные органические вещества растительного и животного происхождения.
2. Органическое вещество специфической природы- гумусовые или перегнойные.
В первую группу входят преимущественно отмершие, но еще не разложившиеся растительные остатки, остатки животных, микроорганизмов.
Во вторую группу входит органическое вещество отмерших растений и животных при благоприятных условиях быстро разлагается микроорганизмами с выделением углекислоты, катионов аммония, калия, кальция и других элементов, а также анионов N03, PO4. Остальная часть разлагающегося органического вещества входит в состав гумуса. В эту же форму переходит значительная часть корневых выделений и продуктов жизнедеятельности микроорганизмов. Гумус является основным источником питательных веществ для растений. Он содержит от 3,5 до 5% азота. Органическое вещество играет важную роль в создании почвенного плодородия и в питании растений.
Новые виды удобрений
Навоз- основное органическое удобрение. Однако в настоящее время его запасы не восполняют потребность почвы в органическом веществе. Поэтому создалась необходимость использования органического удобрения из отходов птицеводства или животноводства с добавкой насыщенного раствора гумата натрия в разных соотношениях, а также органики с минеральными удобрениями.
В последнее время появились научные публикации, посвященные использованию гуматов при выращивании посадочного материала винограда (12-15).
Гуматы- сложные почвенные биопродукты трофических (пищевых) отношений между растениями и почвообразующими микроорганизмами, представляющие собой соли гуминовых кислот. Растения используют их как естественный метаболит. В естественных условиях гуматы возникают в результате процессов гумификации, гидролиза и жизнедеятельности почвенных микроорганизмов. Промышленные способы получения гуматов основаны на реакции получаемых из углей или других сырьевых источников гуминовых кислот со щелочами КОН или NаОН. Гумат натрия является продуктом переработки Нарынкольского угля. Препарат, являясь природным веществом, сходным по строению с гуминовыми кислотами почв не изменяет природу сельскохозяйственных культур, вследствие чего отнесены Госкомиссией к веществам не нуждающимся в гигиеническом нормировании. Гуматы представляют особую группу универсальных регуляторов роста и стрессовых адаптогенов и в этом отношении они не имеют себе равных. Гуматы, в отличие от регуляторов роста не являются фитогорманами и не заменяют работу фитогормонов. Они стимулируют выработку самим растением естественных фитогормонов и активизируют их функциональную деятельность, поддерживая ее на оптимально высоком уровне. Гуматы обладают физиологически активными свойствами, в малых дозах стиулирую рост и деление клеток, обладают антистрессовым эффектом, т.е. повышают устойчивость растений к климатическим, техногенным и прочим стрессам. Гумат натрия усиливает рост корневой системы, а затем надземные массы растений, существенно влияет на образование хлорофилла и фотосинтез.
Особый интерес представляют различные сочетания гуматов с синтетическими регуляторами роста, микроудобрениями. Смешивание гуматов с указанными препаратами обладает ярко выраженным усилением эффекта. Сотрудниками КазНТУ им. К.Сатпаева созданы препараты гуматового класса Шубаршинского месторождения, обогащенные органическим веществом, повышающие адаптогенные свойства препарата.
Для ускоренного размножения оздоровленного посадочного материала, повышения его качества и адаптивности в лаборатории биотехнологии ВНИИВиВ им. Я.И. Потапенко изучаются возможности применения калийного лигногумата. В качестве источника гуминовых веществ использован калийный лигногумат марки AM. Низкомолекулярные соединения гуминовых веществ обладают повышенным биостимулирующим действием на рост и развитие растений, им свойственна высокая миграционная подвижность в почве (15,17) Высокомолекулярные соединения при меньшей миграционной подвижности и невысоком биостимулирующем действии имеют повышенные сорбционные свойства связывания элементов по механизму комплексования, что снижает возможности попадания токсичных и вредных веществ в растение. Эти особенности лигногумата обеспечивают увеличение приспособляемости растений к пестицидному токсикозу и минеральной передозировке, а также позволяют уменьшить последствия стрессовых факторов (пересадки, засухи, переохлаждения). По данным А.Н.Реброва (18) лигногумат в концентрациях 0,1, 0,3 и 0,5 %, оказывал ингибирующее действие. Наряду с ингибирующим действием им было отмечено и положительное действие лигногумата. На субстратах с применением лигногумата раньше образовывались корневые бугорки, и первые корни появлялись (через 7-8 дней) еще до прорастания почек, тогда как на контроле корневая система образовывалась только после появления первых листьев (через 2 недели).
Применение мелиорантов и удобрений в сочетании их с физиологически активными гуминовыми препаратами – адаптогенами, в совокупности с другими агротехническими приемами способствует повышению почвенного плодородия и продуктивности сельскохозяйственных культур, при этом особый интерес представляют различные сочетания гуматов с синтетическими регуляторами роста, микроудобрениями. Смешивание гуматов с указанными препаратами обладает ярко выраженным усилением эффекта.
Инновационное развитие в сфере агрохимии предполагает широкое использование достижений современной биотехнологии, в том числе и применение различных групп биологических препаратов, созданных на основе разных растительных комплексов. Практическим выражением такого подхода стало использование биопрепарата типа ККМ 17. Полученный из бурых углей Нарынкольского месторождения в его состав входит сбалансированный набор макро- и микроэлементов (азот, фосфор, калий, железо, медь, марганец, цинк, кобальт, молибден и другие), а также специальные биодобавки, повышающие адаптогенные свойства препарата, улучшающие плодородие почв. Этот препарат создан в НИИ почвоведения и агрохимии им. У.У.Успанова.
Лекция 8. Азотные удобрения
Азот в изобилии имеется в природе в двух формах: в свободном состоянии в атмосфере земли. Это инертный газ. Он находится также в минеральной и органической форме.
Азот в минеральной форме является одним из основных элементов питания растений, которые могут усваивать его только в этой форме. Азот в органической форме является составной частью живой материи.
Азот стимулирует рост растения. Растение хорошо обеспеченное азотом, растет быстро, образует много листьев и стеблей, приобретает красивую темно-зеленую окраску, благодаря обилию хлорофилла в лиятьях.ю улучшается формирование и развитие репродуктивных органов, что способствует повышению урожайности. По этой причине азот является решающим фактором урожая и основой удобрения.
Однако избыточное азотное питание, особенно в второй половине вегетации, задерживает созревание растений, способствует образованию большой вегетативной массы. Это приводит к снижению урожайности. При обильном азотном питании повышается восприимчивость растений к болезням и вредителям.
При из
