Примеры решения типовых задач. Рассчитайте размер частиц диоксида кремния, если известно
Задача 1.
Рассчитайте размер частиц диоксида кремния, если известно, что время их оседания t на расстояние h = 10-2м составляет 60 мин. Плотности дисперсной фазы ρ = 2,7 ∙ 103 и дисперсионной среды ρ0 = 1 ∙ 10 3 кг/м3; вязкость среды η = 1,5 ∙ 10-3 Па ∙ с.
Решение.
По закону Стокса
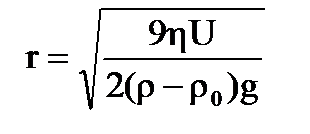 .
.
Скорость седиментации:
U = 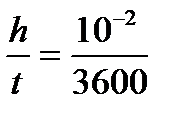 м/с.
м/с.
Размер частиц:
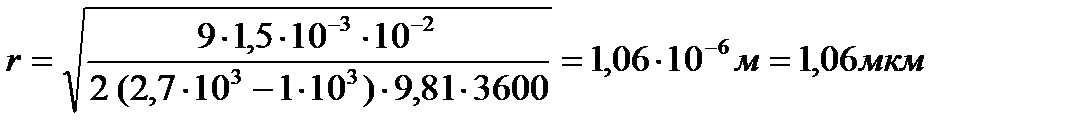 .
.
Задача 2.
В три колбы было налито по 100 мл золя Fe(OH)3. Чтобы вызвать коагуляцию золя, потребовалось добавить в первую колбу 10,5 мл хлорида калия с концентрацией 1моль/л, во вторую − 16,5 мл сульфата натрия с концентрацией 0,01моль/л, в третью – 13,7 мл фосфата натрия с концентрацией 0,001моль/л. Вычислить порог коагуляции каждого электролита и определить знак заряда частиц золя.
Решение.
Вычисляем порог коагуляции для хлорида калия по уравнению 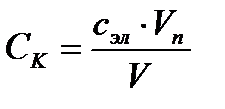 .
.
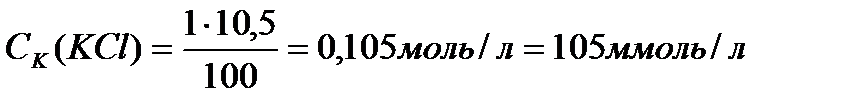 .
.
Аналогично рассчитываем пороги коагуляции для электролитов Na2SO4 и Na3PO4:
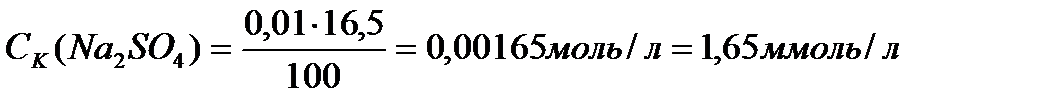 .
.
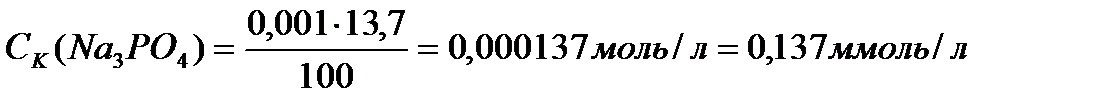 .
.
Электролиты KCl, Na2SO4 и Na3PO4 содержат катионы одинакового заряда, а анионы − разного. Чем заряд иона больше, тем порог коагуляции оказывается меньше. Самый наименьший порог коагуляции и наивысшая коагулирующая способность у ионов PO43-. Следовательно, частицы золя Fe(OH)3 заряжены положительно.
Задача 3.
Пороги коагуляции золя Fe(OH)3 для электролитов KI и K2Cr2O7 соответственно равны 10,0 и 0,195 ммоль/л золя.
Во сколько раз коагулирующая способность дихромата калия больше, чем у иодида калия?
Решение.
Коагулирующие способности электролитов являются величинами, обратными их порогам коагуляции.
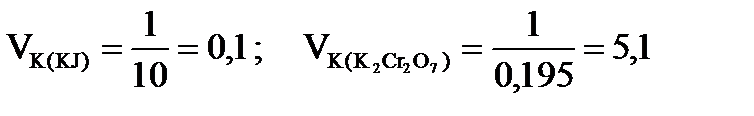 ,
,
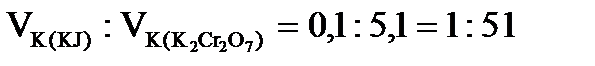 .
.
Для золя Fe(OH)3 коагулирующая способность дихромата калия больше, чем для иодида калия в 51 раз.
Задача 4.
Зная частичную концентрацию золя n0 = 5 ∙ 108 частиц/см3, период коагуляции θ = 335с, рассчитайте общее число частиц Vt , спустя следующее время от начала коагуляции: 100, 200, 250, 350, 400 с.
Постройте график зависимости 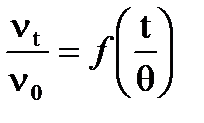 .
.
Решение.
Согласно теории кинетики коагуляции Смолуховского
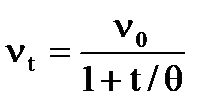 ,
,
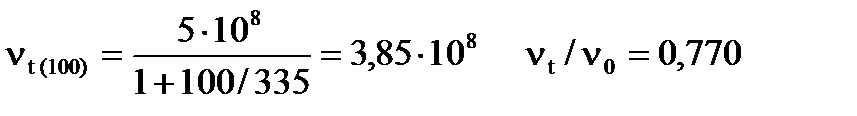 ,
,
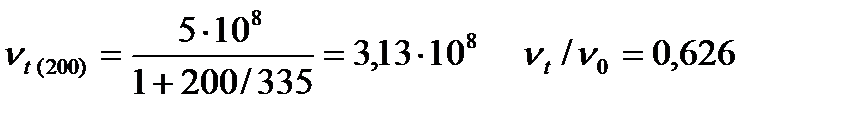 ,
,
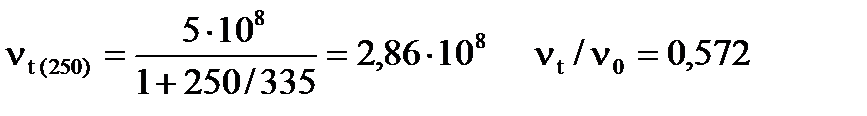 ,
,
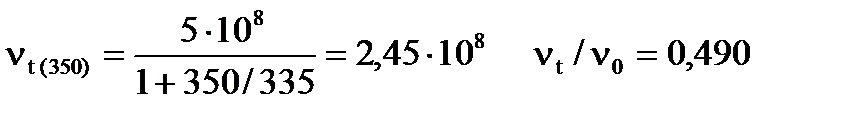 ,
,
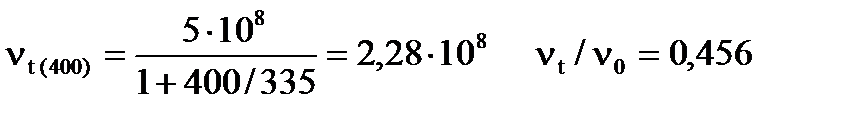 .
.
По полученным данным строим график nt/n0 = f(t/θ).
Задача 5.
Проверьте применимость теории быстрой коагуляции Смолуховского к кинетике процесса коагуляции гидрозоля золота с начальной концентрацией ν0 = 20·1014 частиц/м3.
Определите графически время половинной коагуляции золя θ при температуре T= 300 K. Данные по кинетике коагуляции, где t − время от начала коагуляции, следующие:
t, c 0 30 60 120 240 480
n·10-14, частиц/м3 20,0 14,7 10,8 8,25 4,90 3,00
Решение.
При быстрой коагуляции изменение числа частиц во времени выражается уравнением
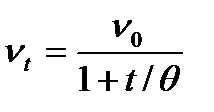 или
или 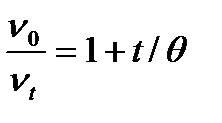 ,
,
где q не зависит от времени коагуляции и является постоянной величиной. Зависимость 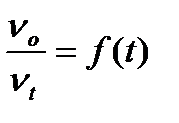 представляет собой прямую, не проходящую через начало координат. Тангенс угла наклона этой прямой к оси абсцисс равен 1/q. Построив график, определяем tg a = 1,25·10-2 и q = 80 c.
представляет собой прямую, не проходящую через начало координат. Тангенс угла наклона этой прямой к оси абсцисс равен 1/q. Построив график, определяем tg a = 1,25·10-2 и q = 80 c.
Теоретическое значение q рассчитываем по уравнению 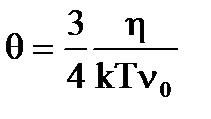 , где k − постоянная Больцмана, k = 1,38·10-23 Дж·K-1, h − вязкость воды равная 1·10-3 Па·с. Тогда
, где k − постоянная Больцмана, k = 1,38·10-23 Дж·K-1, h − вязкость воды равная 1·10-3 Па·с. Тогда
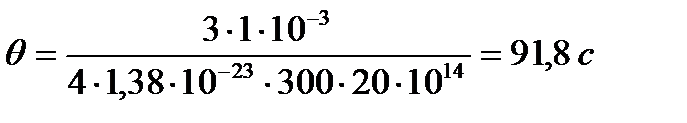 .
.
В пределах ошибок опыта экспериментально найденное значение совпадает с теоретически рассчитанным. Можно считать, что слипание частиц золя золота в данных условиях происходит по типу быстрой коагуляции.
