Механизм окислительно-востановительных процессов
Два атома, которые обмениваются электронами в растворе, представляют собой отдельный гальванический микроэлемент. Атомы играет роль электродов, а вода служит проводником. При отсутствии равновесия между этими электродами имеется разность потенциалов ∆E, которая заставляет электроны переходить от одного атома к другому и тем самым вызывает электрический ток. Величина максимальной полезной работы такого тока пропорциональна переносимому им заряду. Этот заряд равен числу электронов, т.е. стехиометрическому коэффициенту электрона ve в полуреакции,умноженному на число Фарадея Φ (96484,56 Кл×моль-1=23,06 ккал×В-1моль-1=96,55 кДж× В-1моль-1=96487 Дж В-1 г-экв -1). В итоге максимальная полезная работа отдельного гальваничесого микроэлемента j равна:
-DZr,j = ve × Φ ×∆Er,j. (II‑152)
Ту же максимальную полезную работу при отсутствии равновесия в стандартных условиях можно выразить через уравнение изотермы реакции (уравнение Вант-Гоффа):
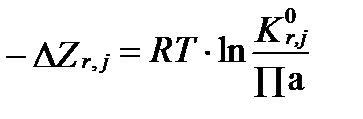 . (II‑153)
. (II‑153)
Уравнения II-147 и II-148 позволяют связать неравновесность окислительно-восстановительной реакции с разностью электрических потенциалов. Приравняв эти уравнения, получим значение электроического потенциала между взаимодействующими атомами-электродами j в стандартных условиях, как функцию их химической неравновесности:
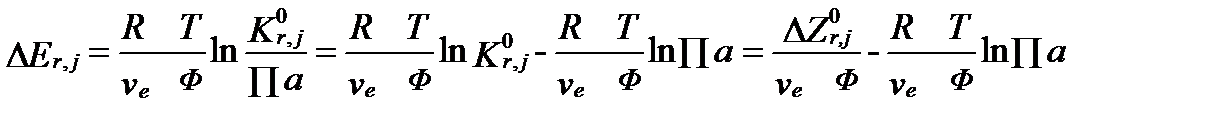 . (II‑154)
. (II‑154)
Согласно этому уравнению напряжение (электродвижущая сила) между атомами-электродами, определяется суммой двух слагаемых.
Первое слагаемое характеризует электрический потенциал окислительно-восстановительной реакции, когда все её компоненты имеют активности равные 1, и второе слогаемое равно 0. Это означает, что первое слагаемое определяет напряжение между атомами редокс-пары j, представленными в виде чистого вещества, в стандартных условиях. Для ионов такими чистыми веществами служат растворы с концентрацией в 1 моль/кг (моляльность), а для газовых компонентов - с парциальным давлением 1 атм (100 кПа). При этом коэффициенты активности в них равны 1. Величина этого первого слагаемого:
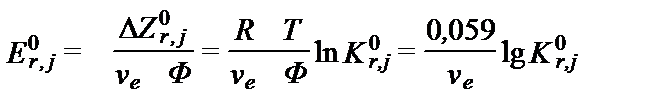 , (II‑155)
, (II‑155)
называется стандартным (нормальным) потенциалом реакции (standard electrode potential). Этот стандартный (нормальный) потенциал характеризует разность потенциалов редокс-пары j при активностях равных 1. Он фактически является термодинамической константой равновесия реакции, выраженной в единицах напряжения (вольтах или милливольтах).
Второе слагаемое характеризует отклонение реального напряжения между элементами редокс-пары j в растворе от стандартного потенциала их реакции 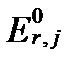 вследствие разницы между реальными и стандартным условиями.
вследствие разницы между реальными и стандартным условиями.
Общее уравнение электрического напряжения между атомами любой редокс-пары j имеет вид:
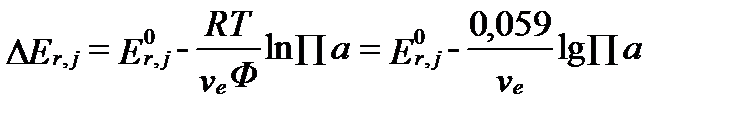 . (II‑156)
. (II‑156)
Это уравнение характеризует реальное напряжение между элементами редокс-пары и обычно называется уравнением Нернста (Nernst equation), в честь его автора Вальтера Германа Нернста (1864-1941).
Если в этом уравнении активности выразить через концентрации и коэффициенты активности, то получим:
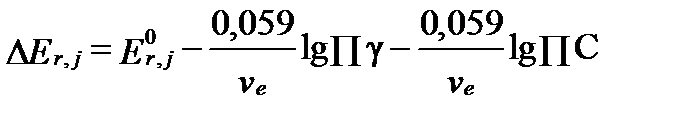 . (II‑157)
. (II‑157)
Первых два слагаемых в этом уравнении справа:
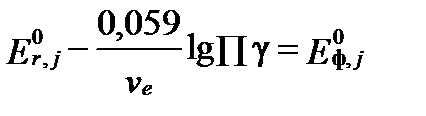 (II‑158)
(II‑158)
называют формальным стандартным потенциалом (formal standard potential). Тогда уравнение Нернста принимает вид:
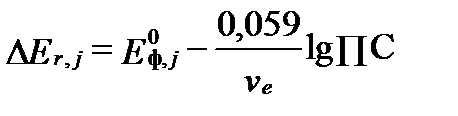 . (II‑159)
. (II‑159)
В разбавленых растворах, где коэффициент активности почти равен 1, 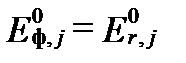 , и формальный потенциал практически равен стандартному. Точность такого приближения для многих расчетов оказывается достаточной.
, и формальный потенциал практически равен стандартному. Точность такого приближения для многих расчетов оказывается достаточной.
Часто окислительно-восстановительный потенциал удобно выражать не величиной электрического потенциала, а непосредственно активностью электронов ae, участвующих в реакции. Для этого в произведение активность вводят активность электронов и рассматривают её, как самостоятельный сомножитель:
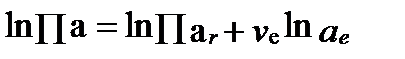 . (II‑160)
. (II‑160)
В этом уравнении Πar характеризует произведение активностей всех компонентов, кроме электронов реакции, а величина ve (положительная при окислении и отрицательная при восстановлении) отражает число электронов, участвующих в полуреакции. Тогда уравнение II-151 примет вид:
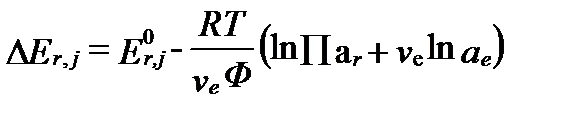 . (II‑161)
. (II‑161)
Когда в стандартных условиях ΔEr,j = 0 и все взаимодействующие компоненты, кроме ae,имеют концентрации 1моль/кг (моляльность). Тогда:
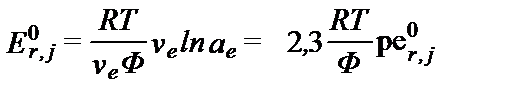 . (II‑162)
. (II‑162)
В этом уравнении величина 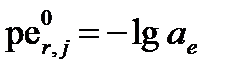 и характеризует активность электронов эквивалентную стандартному потенциалу реакции
и характеризует активность электронов эквивалентную стандартному потенциалу реакции 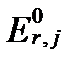 . Из него следует, что если напряжение
. Из него следует, что если напряжение 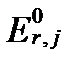 выражено в вольтах, то
выражено в вольтах, то
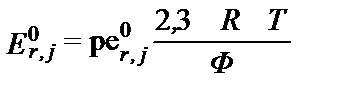 и
и 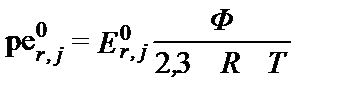 , (II‑163)
, (II‑163)
а в стандартных условиях (при температуре 25oC) имеем:
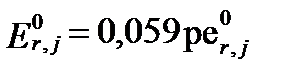 , а
, а 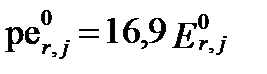 . (II‑164)
. (II‑164)
Величина 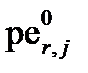 характеризует концентрацию электронов в электронных оболочках атомов одной редокс-пары, при которой их компоненты находятся в равновесии, а
характеризует концентрацию электронов в электронных оболочках атомов одной редокс-пары, при которой их компоненты находятся в равновесии, а 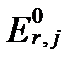 – электрическое напряжение при этой концентрации. Сравнивая уравнения II-150 и II-159, получим
– электрическое напряжение при этой концентрации. Сравнивая уравнения II-150 и II-159, получим
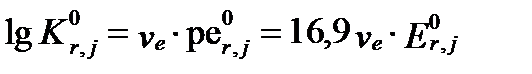 . (II‑165)
. (II‑165)
Таким образом, величины 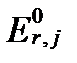 ,
, 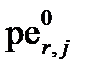 , и
, и 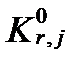 представляют собой разные формы выражения константы равновесия отдельных окислительно-восстановительных реакций. Первая из них измеряется в вольтах электрического напряжения, а остальные представляют собой безразмерные величины. Обычно в качестве константы равновесия окислительно-восстановительных реакций используют их стандартные потенциалы, выраженные в вольтах.
представляют собой разные формы выражения константы равновесия отдельных окислительно-восстановительных реакций. Первая из них измеряется в вольтах электрического напряжения, а остальные представляют собой безразмерные величины. Обычно в качестве константы равновесия окислительно-восстановительных реакций используют их стандартные потенциалы, выраженные в вольтах.
