Исследование влияния переменной нагрузки на реакции связей

Если одна из сил, действующих на систему, является переменной, то реакции связей также будут изменяться и решение системы становиться чрезвычайно трудоемким. Закономерность изменения реакций связей в этом случае следует определять с помощью встроенного в систему вычислительного блока команд Given...FricFac...Find. Что означает нахождение неизвестных реакций связей для частного значения аргумента с присвоением их переменным с индексом.

Влияние изменяющейся нагрузки на реакции связей можно тут же наглядно представить, воспользовавшись графическим редактором системы Mathcad.

Для реализации программы расчета реакций пространственной системы сил с изменяющейся нагрузкой введем новую переменную и выразим через нее дискретное значение аргумента. Например, если сила F изменяется по направлению в горизонтальной плоскости от 0 до 180°, то, введя переменную i, дискретно изменяющуюся от 0 до 18 с шагом 1, можно выразить силу F через дискретное значение аргумента f_i.

Таким образом, аргумент и функция примут вид:

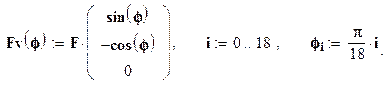Главный вектор иглавный момент системы также должны быть представлены в этом случае как функции аргумента f:

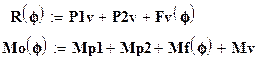В этом случае программа расчета реакций пространственной системы сил с использованием векторной формы геометрических и силовых (с изменяющейся нагрузкой) параметров в системе Mathcad примет вид, показанный ниже.

Программа расчета реакций с использованием численного метода

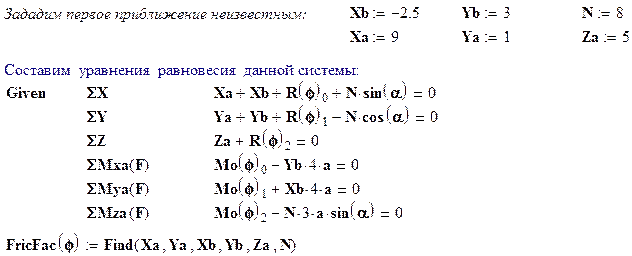( случай изменяющейся нагрузки)

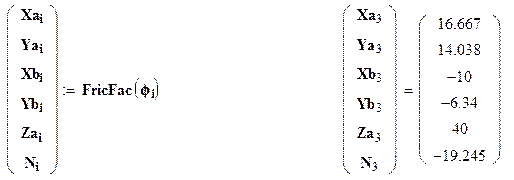Заканчивается вычислительный блок выводом неизвестных реакций связей для частного значения аргумента с присвоением их переменным с индексом.

Вызвав графический редактор системы Mathcad, покажем влияние изменяющейся по направлению силы F на реакции связей в функции угла f.

Самоконтроль осуществляется сравнением результатов расчета, полученных различными методами, что и подтверждает правильность решения задачи.

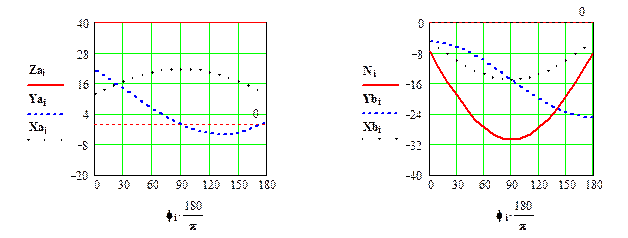Рис. 1.2. Влияние угла наклона силы - F на реакции в опорах

Проверкой усвоения материала являются самостоятельно выполненное контрольное задание по данной теме.

Варианты заданий по теме пространственная система сил

Две однородные тонкие плиты (схема 1.1 – 1.7, табл. 1.1) жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником ) в точке А, цилиндрическим шарниром (подшипником) в точке Ви невесомым стержнем 1;или же двумя подшипниками в точках А и В и двумя невесомыми стержнями 1 и 2 (схема 1.6, 1.8 - 1.10). Все стержни прикреплены к плитам и к неподвижным опорам шарнирами.

Размеры плит указаны на рисунках; вес большой плиты Р1=5 кН, вес меньшей плиты Р2=3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость xy -горизонтальная).

На плиты действуют пара сил с моментом М=4 кНм, лежащая в плоскости одной из плит, и две силы. Значение этих сил, их направления и точки приложения указанны в таблице 1.1; при этом силы F1 и F4 лежат в плоскостях xy, сила F2 в плоскости, параллельной xz, и сила F3 в плоскости, параллельной yz. Точки приложения сил(D, E, H, K) находятся в углах или в серединах сторон плит.

Определить реакции связей в точках A и B и реакцию стержней.

Указание. При решении задач на равновесие тела под действием произвольной пространственной системы сил необходимо учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) - две составляющие, лежащие в плоскости, перпендикулярной оси подшипника. При вычислении момента от действия сил удобно разложить ее на три составляющие, параллельные координатным осям и представить их в векторной форме. Координаты приложения действующих на систему сил, также должны быть представлены в векторной форме.

Начинать решение задачи следует с составления шести уравнений равновесия плит под действием пространственной системы сил.

Для прочного усвоения материала рекомендуется решить задачу, как аналитическим методом, так и численным, несмотря на то, что решать подобные задачи с использованием компьютерных технологий численным методом несравненно проще.

При подсчетах принять a=0,5 м.

Таблица 1.1.