Кинетика поликонденсации

Рассмотрим основные кинетические закономерности поликонденсации на примере полиэтерификации. Катализаторами реакции этерификации являются кислоты и щелочи. Механизм кислотного катализа к настоящему времени надежно установлен. Он включает две стадии:

1. Протонирование кислоты-реагента кислотой-катализатором (НА):

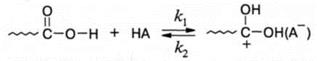
2. Атаки протонированным реагентом гидроксильной группы спирта с последующим распадом интермедиата до продуктов реакции:

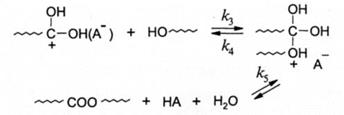
Если в данной реакции удалять воду, то можно учитывать лишь прямое направление реакции. Тогда:

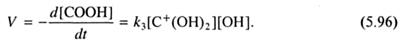
Неопределяемая величина [С⁺(ОН)₂] может быть исключена с помощью выражения (5.97):

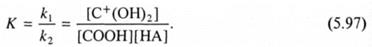
В результате получаем:

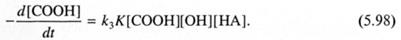
В отсутствие внешнего катализатора его функцию выполняет кислота-мономер. Тогда:

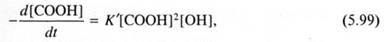
где К' = k₃К. Поскольку при поликонденсации концентрации разных функциональных групп обычно равны (в целях получения высокомолекулярного полимера), то уравнение (5.99) можно упростить:

Интегрирование этого уравнения приводит к выражению:

и далее, с использованием понятия степени завершенности реакции (5.88), приходим к конечному результату:

Уравнение (5.102), исходящее из третьего порядка скорости по концентрации мономера, достаточно хорошо описывает экспериментальные данные. Встречающиеся отклонения при средних и глубоких степенях завершенности связаны с изменением состояния реакционной среды - уменьшением полярности, вследствие исчерпания карбоксильных и гидроксильных (или других полярных) групп мономеров, и возрастанием вязкости.

Степень ступенчатой полимеризации равна числу мономерных звеньев в цепи. При ступенчатой полимеризации двух гомофункциональных мономеров A-R-A и B-R-B степень полимеризации равна половине их количества в цепи. Сочетание (5.92) и (5.102) приводит к зависимости степени полимеризации от времени:

Из этого уравнения следует, что темп нарастания молекулярной массы продукта поликонденсации уменьшается со временем. Данную зависимость не следует путать с той, что вытекает из уравнения Карозерса (5.92), согласно которому темп возрастания 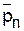с ростом конверсии увеличивается.

Изложенное выше касалось самокатализируемой поликонденсации. При наличии специально введенного, так называемого внешнего катализатора, уравнение скорости отвечает второму порядку по концентрации мономера:

Интегрирование (5.104) приводит к (5.105) и далее с использованием (5.92) к уравнению (5.106):

Из уравнения (5.106) следует, что при катализируемой поликонденсации имеет место линейная зависимость степени полимеризации от времени.

На практике самокатализируемая реакция используется при получении полиамидов, тогда как при получении полиэфиров и фенопластов - продуктов поликонденсации фенола с формальдегидом - применяется катализатор.

При предыдущем изложении предполагалось равенство концентраций мономеров, что является одним из условий получения высокомолекулярного полимера при поликонденсации. Количественной мерой, отражающей степень эквивалентности концентраций мономеров, является параметр

вследствие [M₁] ≥ [M₂]. Связь среднечисловой степени полимеризации с параметром эквивалентности дается выражением:

При строго эквивалентных количествах функциональных групп на концах макромолекул реакция между ними может продолжаться сколь угодно долго, теоретически - вплоть до образования гигантской макромолекулы. Из этого следует, что для стабилизации молекулярной массы полимера небольшой избыток одного из мономеров может оказаться полезным. В этом случае все макромолекулы будут иметь одинаковые функциональные группы, например 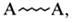что исключает возможность реакции между ними. Для этих целей используют также малые добавки монофункционального соединения. При этом уравнение (5.108) по-прежнему применимо, однако параметр r рассчитывается по-другому. При поликонденсации двух гомофункциональных мономеров ARA и BR₁B в присутствии монофункционального соединения R₂B

где [ARA] = [BR₁B]. Коэффициент 2 вводится потому, что эффект добавки R₂B аналогичен эффекту избытка бифункционального мономера BR₁B, a уравнение (5.109) получено применительно к реакции двух бифункциональных мономеров. При поликонденсации одного гетерофункционального мономера ARB в присутствии BR₁