Уравнение состояния. Термодинамическая характеристика раствора
В том случае, когда нужно охарактеризовать осмотическое давление раствора полимера в достаточно широком диапазоне концентраций, раствор нельзя рассматривать как идеальный с невзаимодействующими молекулами растворенного вещества. Химический потенциал растворителя в реальном растворе наилучшим образом может быть представлен степенным рядом, т.е. путем вириального разложения.
Применительно к разбавленному реальному раствору указанный подход приводит к следующему выражению для химического потенциала растворителя:
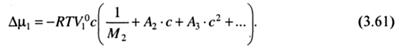
Исходя из (3.61) и с учетом (3.56), зависимость осмотического давления раствора от концентрации растворенного вещества будет представлена следующим выражением:
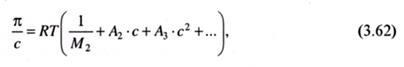
где А1, А2, ... или соответствующие им В, С, ... в других, также принятых обозначениях, являются константами, зависящими от температуры и природы растворенного вещества, которые называются вириальными коэффициентами.
Для теории растворов полимеров особое значение имеет второй вири-альный коэффициент, обозначаемый как А2 или В. Под первым вириальным коэффициентом подразумевается первый член в скобках уравнения (3.61), равный 1/М2.
Значения вириальных коэффициентов могут быть определены, исходя из выражения для химического потенциала растворителя, полученного как конечный результат теории Флори-Хаггинса. Из (3.42) с учетом (3.56) имеем:
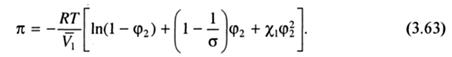
При малых концентрациях полимера член ln(1 - φ2) можно разложить в ряд по степеням φ2, тогда:
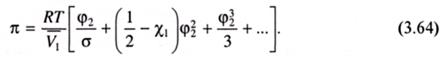
где ρ1, ρ2 - плотности растворителя и полимера; М1 - молекулярная масса растворителя. При достаточно малой концентрации полимера членами ряда в скобках, начиная с третьего, в уравнении (3.65) можно пренебречь, тогда:
Уравнения (3.65), (3.68) относятся к уравнениям состояния, поскольку они связывают значения параметров раствора и его термодинамических характеристик со свойствами, доступными для измерения, в данном случае - с осмотическим давлением.
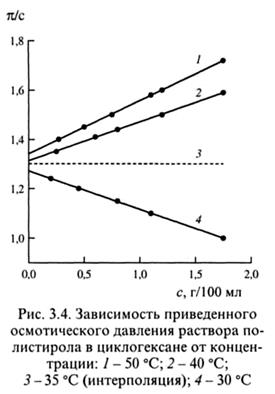
Зависимость, вытекающая из уравнения (3.68), используется для термодинамической характеристики качества растворителя в растворе. На рис. 3.4 приведены три возможных случая:
кривые 1,2 А2 > 0,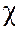 
< 1/2 - хороший растворитель;
кривая 3 А2 = 0, 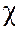= 1/2 - идеальный растворитель;
кривая 4 А2 < 0, 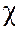> 1/2 - плохой растворитель.
Экспериментально найдено, что в хороших растворителях величина А2 обратно пропорциональна молекулярной массе полимера в степени 0,05 - 0,25, т.е. А2 ~ 1/М0,1. Напомним, что состояние, отвечающее термодинамически плохому растворителю, реализуется в очень узком интервале, т.к. при Т < θ раствор становится термодинамически неустойчивым и разделяется на две фазы.