Результаты измерений и их достоверность

Наблюдаемые значения представляют собой только исходный материал, использумый для обоснования величин показателей свойств и состава подземных вод. Величины показателей свойств и состава, расчитанные на основании наблюдамых значений, представляют собой результаты измерений (measuring result). Если наблюдаемое значение одно, оно и являтся результатом измерения. Чем больше наблюдаемых значений использовано в обосновании результата измерений, тем выше достоверность последнего. Определение результатов измерений регламентируется и, согласно ГОСТ’у Р ИСО 5725-1-2002, зависит от числа (одно или несколько) наблюдаемых значений, способа их усреднения (среднее арифметическое значение, медиана, стандартное отклоне­ние и т.д.) и формы представления. Иногда требуется введение стандартных поправок (например, таких как приведение объема газа к нормальной температуре и давлению). Согласно ГОСТ’у Р 51592-2000, результаты измерений характеризуются двумя величинами: математическим ожиданием идоверительным интервалом, т.е. в форме .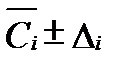

Химический потенциал

Максимальная полезная работа согласно этому уравнению достигает своих значений только в условиях обратимости, т.е. термодинамического равновесия, когда величины ΔS, ΔU и ΔV бесконечно малы. Это значит, что максимальная полезная химических процессов равна:

. (II‑33)

В этом случае максимальная полезная работа является такой же функцией состояния, как и остальные параметры, и может быть использована наравне с ними.

Химический потенциал

В последнем уравнении II-33 максимальная полезная работа химических процессов в растворе W_z зависит от величины 5 параметров состояния. Для её измерения число этих переменных сокращают до 3. Для этого термодинамические процессы рассматривают в условиях, где, величины, как минимум, 2 параметров состояния не меняются. Тем самым они исключаются из интегрального уравнения, как переменные. Однако, такими параметрами могут быть только те, которые можно стабилизировать и контролировать в процессе эксперимента.

Визохорно-адиабатных условиях, когда dV = 0 и dS= 0, максимальная полезная работа обратимого процесса

W_z,max= –∫dU = – (∆U)_S,V = – (U₂ –U₁)_S,V. (II‑34)

Это значит, что в изохорный-адиабатических условиях величина максимальной полезной работы равна изменению внутренней энергии U. Поэтому внутреннюю энергию также называют изохорно-адиабатным потенциалом (isochoric adiabatic potential). Однако обеспечивать постоянство объема и, тем более, энтропии системы крайне сложно.

В изобарно-адиабатных условиях, когда dP=0 и dS=0, максимальная полезная работа обратимого процесса равна

W_z,max= – ∫U– ∫PdV = – (∆U+P∆V)_S,P = – (U₂+ PV₂ ) – (U₁+PV₁)_S,P . (II‑35)

Эта сумма внутренней энергии и работы U+PV называется энтальпией (enthalpy)и обозначается обычно символом H,

W_z,max = – (H₂–H₁)_S,P= – (∆H)_S,P.

Это значит, что энтальпия является изобарно-адиабатным потенциалом, т.е. мерой максимальной полезной работы при постоянстве давления и энтропииОднако сохранять и контролировать постоянство энтропии в реальных условиях сложно.

В изохорно-изотермических условиях, когда dT=0 и dV=0, максимальная полезная работаравна

W_z,max=∫TdS -∫dU = ∆(TS – U)_T,V = ( TS₂ – U₂) _T,V – (TS₁- U₁)_T,V. (II‑36)

Разность U – TS =F характеризует экстенсивное свойство, которое называют изохорно-изотермическим потенциалом (potential isochoric -isotermal). Этот потенциал ввел в 1882 г. Герман Людвиг Гельмгольц (1821-1894). Так как теплота TS рассматривается, как связанная энергия, он назвал его свободной энергией (free energy). Часто этот потенциал называют свободнаяэнергией Гельмгольца (Helmholtz free energy). Таким образом, в изохорно-изотермических условиях максимальная полезная работа является функцией изменения свободной энергии или энергии Гельмгольца:

W_z,max= – (∆F)_V,T. (II‑37)

Но и эти условия сложно соблюдать из-за невозможности исключить тепловое расширение системы.

Наконец, в изобарно-изотермических условиях, когда dP=0 и dT=0, максимальная полезная работа равна

W_z,max= ∫TdS - ∫dU - ∫PdV= –∆(U+PV –TS)_P,T = – (U₂ +PV₂ –TS₂)– (U₁+ PV₁–TS₁)_P,T. (II‑38)

Сумма U +PV –TS = F+PV = H – TS = Z характеризует экстенсивное свойство, называемое изобарно-изотер­мическим потенциалом (potential ) . Этот потенциал был введен в 1874 Джозайем Уиллардом Гиббсом (1839-1903) и первоначально назван им также свободной энергией, что вызвало путаницу. Чтобы ввести порядок этот потенциал называли свободной энергией Гиббса (Gibbs free energy). По своему содержанию он представляет собой энтальпию без связанной энергии. Поэтому изобарно-изотермический потенциал часто называют свободной энтальпией (free enthalpy). Отсюда следует, что в изобарно-изотермических условиях мерой максимальной полезной работы является свободная энтальпия:

W_z,max= – (∆Z)_P,T. (II‑39)

Этот потенциал характеризует изменение энергии при постоянстве температуры и давления системы, параметров, которые относительно легко мерить и контролировать.

Итак, интересующая нас максимальная полезная работа может быть измерена как функция изменения внутренней энергии, энтальпии, свободной энергии или свободной энтальпии. Но в практике термодинамических исследований наиболее удобной и используемой является свободная энтальпия.

В связи с этим полезная работа самопроизвольных химических реакций измеряется в величинах свободной энтальпии, которые в реальных условиях связаны неравенством:

W_z < – (∆Z)_P,T. (II‑40)

Лишь в одном случае полезная работа самопроизвольных химических реакций достигает максимального значения. Таким случаем является термодинамическое равновесие, для которого справедливо равенство

, (II‑41)

где ΔZ_i – свободная энтальпия изменения концентрации каждого компонента с порядковым номером i.

Согласно этому уравнению средняя парциальная величина характеризует увеличения свободной энтальпии раствора при добавлении в него 1 моля каждого компонента i и равна:

. (II‑42)

Тогда частной производной изменения свободной энтальпии при изменении состава раствора будет:

, (II‑43)

т.е. истинной парциальной величиной свободной энтальпии (свободной энергии Гиббса), называемой химическим потенциалом (chemical potential).

Строго говоря, химический потенциалхарактеризует изменение энергии раствора при изменении содержания любого компонента i на бесконечно малую величину в условиях обратимых процессов. В общем случае химическийпотенциал может быть определён, как изменение величины любого термодинамического потенциала (внутренней энергии U при dV = 0 и dS= 0, энтальпии H при dP=0 и dS=0, свободной энергии F при dT=0 и dV=0, свободной энтальпии Z при dP=0 и dT=0) за счёт изменении содержания только одного компонента i. Таким образом:

(II‑44)

Однако, чаще пользуются химическим потенциалом, выраженным через свободную энтальпию. Тогда, согласно первому уравнению Гиббса-Дюгема, свободная энтальпия всего раствора равна:

, (II‑45)

а для 1 моля раствора:

, (II‑46)

где C_j –мольная доля компонента i. Если раствор состоит только из одного соединения H₂O, то его свободная энтальпия Z_моль= . Так как в этом случае мольная доля =1, свободная энтальпия будет равна средему химическому потенциалу чистого вещества, Z = . Поэтому изменение свободной энтальпии раствора вследствие изменения его остава можно принять равным:

, (II‑47)

или для одного моля раствора:

(II‑48)

Согласно второму уравнению Гиббса-Дюгема имеем:

. (II‑49)

Это уравнение Гиббса-Дюгема связывает изменения химических потенциалов разных компонентов раствора между собой. Действительно, если в растворе присутствуют только два компонента, то имеем уравнение:

N₁dm₁ + N₂dm₂ = 0. (II‑50)

Это означает, что если при постоянной температуре и давлении химический потенциал одного компонента увеличивается, то потенциал другого должен уменьшаться.

Химический потенциал, как и концентрация, является интенсивным параметром и не зависит от количества раствора. Он служит основным критерием равновесности состава и состояния систем. Именно градиент химического потенциала, а не концентраций является движущей силой массообмена подобно тому, как градиент давления является движущей силой фильтрации. Равновесие достигается тогда, когда не концентрации, а химические потенциалы растворенных компонентов уравниваются во всём объеме среды или в сравниваемых средах. При равных химических потенциалах концен­трации компонен­тов могут быть совершенно разными. Поэтому для определения скорости и направленности химических процессов или массообменов необходимо уметь измерять величины химических потенциалов.

Термодинамические концентрациии