Учет сольватации в квантовохимических расчетах

КЛАССИФИКАЦИЯ МОДЕЛЕЙ

Большинство органических реакций протекает в жидкой фазе. Очень часто растворитель изменяет не только выходы конечных продуктов, но и механизм реакции. В газовой фазе многие реак­ции идут по радикальному механизму, а в растворе - по ионному. Поэтому при квантовохимическом изучении реакционной способно­сти органических соединений необходимо учитывать взаимодейст­вие со средой.

В основе современных представлений о взаимодействии раство­ренных соединений с растворителем лежат ставшие классическими работы Борна, Дебая, Леннард-Джонса, Лондона, Кирквуда и Онзагера. Эти работы, их дальнейшее развитие и роль в химии подробно проанализированы в монографии [84]. Однако исполь­зовать непосредственно приведенные там результаты для учета сольватации в квантовохимических расчетах не удается, поэтому были разработаны более простые модели, которые позволяют рас­считать энергию сольватации с достаточно высокой степенью точ­ности. Прежде чем перейти к описанию этих моделей, рассмотрим возможные типы сольватации.

Сольватацию принято разделять на два типа - специфическую и неспецифическую. Для первой характерно существование в ра­створах структурно-определенных образований между сольватом и сольвентом, время жизни которых заметно превышает период сво­бодного колебания этой выделенной системы. Примерами подобных образований являются водородные связи, комплексы с переносом заряда и т.д. Для всех них характерны структурная определенность и относительно большая величина энергии взаимодействия, которая может иногда превышать 10% от энергии химической связи, а также существенное перераспределение заряда между растворенным соеди­нением и растворителем.

Несколько особняком лежит случай сольватации малых одно-, двух- и некоторых трех- и четырехатомных ионов. Для этих соединений характерны все перечисленные особенности, но связь оказывается необычайно прочной. Так, энергия гидратации ОН ^- составляет 445 кДж/моль, Н₃О⁺ 382 кДж/моль, NH₃ 344 кДж/моль. Такие структуры, по-видимому, было бы правильнее рассматривать как координированные.

В случае неспецифической сольватации энергия взаимодействия между растворенным соединением и молекулами растворителя неве­лика и не может создать сольватационные оболочки с жестко-фиксированной структурой. Основной вклад в энергию сольва­тации этого типа вносят ван-дер-ваальсово взаимодействие и элект­ростатическое взаимодействие дипольных моментов растворенного соединения и молекул растворителя.

Методы квантовой химии, которые в настоящее время исполь­зуются для описания сольватационных эффектов, можно разделить на две большие группы, дискретные и континуальные. Дискретные подходы обычно имеют дело с описанием какого-либо выделенного объема системы растворенное соединение-растворитель с вклю­чением до десяти молекул последнего. Эти молекулы располагают вокруг растворенного соединения в определенной системе (при­ближение "супермолекулы", различные варианты модели точечных диполей или зарядов). Подобное описание близко к химическому определению специфической сольватации. Они различаются лишь тем, что в расчет частично включается неспецифическое взаимо­действие растворенного соединения и растворителя.

В некоторых работах рассматривались дискретные системы, со­держащие 200-300 молекул растворителя (метод Монте-Карло с атом-атомными потенциалами). Такие большие кластеры пригодны для описания как специфического, так и неспецифического взаимо­действия растворенного соединения с растворителем. Однако рас­четы для них связаны с очень большими затратами машинного времени. Поэтому для учета неспецифической сольватации широ­кое распространение получили континуальные модели (сольватонная модель, модель самосогласованного поля реакции). В них не учитывается микроскопическая структура растворителя, поэто­му отпадает необходимость определять строение сольватационной оболочки. Благодаря этому расчет становится существенно проще.

Полную энергию молекулы в растворителе можно представить как сумму двух отдельных вкладов: Е_полн= Е_М + Е_С ,

где Е_М — энергия изолированной молекулы; Е_С — энергия сольвата­ции. В предположении отсутствия специфического взаимодействия между растворенным соединением и растворителем, т.е. существенно­го перераспределения заряда между ними (этот случай будет рассмот­рен отдельно), Е_С является суммой трех вкладов:

Е_С = Е_эл + Е_дисп + Е_кав.

где Е_эл - энергия электростатического взаимодействия между соб­ственными и наведенными зарядами растворенного соединения и мо­лекулами растворителя;

Е_дисп - дисперсионная составляющая энергии взаимодействия, учитывающая ван-дер-ваальсово взаимодействие; Е_кав - так называемая кавитационная энергия, т.е. энергия реорганизации растворителя, необходимая для образования полости, в которой поме­щается растворенное соединение. Расчеты с учетом всех трех вкла­дов в энергию сольватации показали, что для наиболее интерес­ных полярных и заряженных систем в полярных растворителях, когда сольватация может существенно изменить результаты газо­фазных расчетов, Е_эл превышает Е_дисп и Е_кав; кроме того, ока­залось, что именно Е_эл существенно изменяется в ходе реакции, а небольшие изменения Е_дисп и Е_кав в значительной мере компен­сируют друг друга. Это привело к разработке ряда моделей, в кото­рых сольватация учитывается в электростатическом приближении (различные варианты модели точечных диполей или зарядов, боль­шинство континуальных моделей).

В настоящее время предложено много разных способов учета сольватации. Ниже будут рассмотрены лишь те из них, которые получили наиболее широкое распространение.

2.2. СОЛЬВАТОННАЯ МОДЕЛЬ

Эта модель была предложена Джано [85] и Клопманом [86]. В ее основе лежит предположение, что с каждым атомом рас­творенного соединения связан индуцированный в растворителе элект­рический заряд - сольватон. Заряд сольватона по абсолютной ве­личине равен заряду на атоме, который его индуцировал, но имеет противоположный знак. Сольватоны не взаимодействуют между собой. Энергия взаимодействия между сольватоном С и атомом А вы­числяется по следующей формуле:

E_СА=q_Cq_Aе²(ε - 1)/(2rε)

где r — радиус атома А, если сольватон С индуцирован зарядом данного атома, или расстояние между атомами А и В, если сольва­тон индуцирован зарядом атома В;

q_C и q_А — заряды сольватона С и атома А в единицах заряда электрона;

е - заряд электрона; ε - диэлектрическая проницаемость среды.

Чаще для оценки Е_СА исполь­зуют аналогичное выражение с кулоновскими интегралами, взя­тыми из квантовохимического расчета, т.е. е²/r полагается равным γ_АА, если сольватон С индуцирован зарядом на атоме А, или γ_АB, если сольватон С индуцирован зарядом атома В (γ_АA и γ_АB — одно- и двухцент­ровые кулоновские интегралы соответственно; см.разд. 1.2). Для энергии сольватации в этом приближении можно записать следующее выражение, где сумма берется по всем атомам растворенной молекулы:

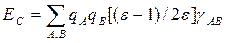
В качестве примера использования сольватонной модели для изучения механизмов органических реакций рассмотрим результа­ты работы [87], в которой изучена Z,E-изомеризация α,β-дизамещенных α,β-непредельных альдегидов.

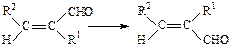
Расчеты были проведены методами ППДП/2 и МЧПДП/3. Эта реакция связана с внутренним вращением вокруг двойной связи С=С и в газовой фазе идет с очень высоким активационным барье­ром 200 - 250 кДж/моль. Преодолеть такой активационный барьер при нормальных условиях очень трудно, поэтому скорость газо­фазной реакции будет ничтожно мала.

Для реакции в растворе можно предложить следующие два механизма катализа, которые позволяют снизить активационный барьер.

1. Если растворитель обладает кислотными свойствами, то ста­новится возможной протонизация исходного соединения, после чего по данным квантохимических расчетов активационный барьер реак­ции должен уменьшиться до 105 - 110 кДж/моль.

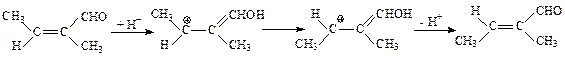
Учет влияния растворителя с использованием сольватонной мо­дели (величина ε полагалась равной 5 и 10) приводит к допол­нительному понижению высоты активационного барьера, и он ста­новится равным 75 - 85 кДж/моль. Реакции с таким активацион­ным барьером могут проходить при нормальных условиях. Таким образом, если растворитель обладает кислотными свойствами, то он может существенно ускорить реакцию Z,E-изомеризации α,β-дизамещенных α,β-непредельных альдегидов.

2. Если растворитель способен катализировать перенос атома Н от группы СН₃ к СО, то становится возможным второй меха­низм увеличения скорости изомеризации:

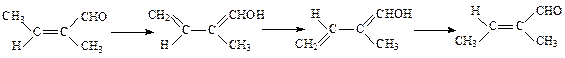
Высота активационного барьера изомеризации, проходящей по второму механизму, определяется высотой активационного барье­ра переноса протона от группы СН₃ к карбонильному кисло­роду. Эта реакция, согласно результатам квантовохимических рас­четов в газовой фазе, требует затраты около 65 кДж/моль. Учет сольватации повышает эту величину до 80 кДж/моль. Если раст­воритель обладает хорошей способностью к переносу протона (та­кой же, как вода), то высота активационного барьера будет близ­ка к тепловому эффекту реакции, т.е. активационный барьер будет немногим выше 80 кДж/моль. С таким активационным барьером реакция может проходить при нормальных условиях.

Сольватонная модель проста и экономична. Однако она обла­дает рядом серьезных недостатков. Самый неприятный из них заключается в том, что сольватоны локализуются в непосредст­венной близости от атомов растворенной молекулы, которые их индуцировали, т.е. фактически проникают внутрь молекулы. В слу­чае ионов сольватонная модель учитывает изменение энергии соль­ватации только за счет изменения степени делокализации заряда, хотя в действительности определяющим фактором в данном случае является их объем. Если изменение степени делокализации заряда коррелирует с изменением объема иона, то сольватонная модель будет давать правильные результаты. Из этого становятся ясными ограничения области ее применения. В частности, сольватонная модель не может учесть эффекты экранирования заряда неполяр­ными группами или молекулами реагентов. По этой причине ее нельзя применять в комбинации с приближением "супермолекулы" при необходимости учесть эффект специфической сольватации.

В заключение настоящего раздела отметим еще одно важное обстоятельство. Выше было указано, что заряды на атомах, вы­численные разными методами, сильно различаются. Из-за этого сольватонная модель, будучи примененной в рамках разных ме­тодов, дает разные результаты. Она неплохо работает с методом ППДП/2. Мы пробовали использовать ее также в расчетах мето­дами МЧПДП/2, МЧПДП/3 и МПДП, но результаты получились гораздо хуже.

2.3. МОДЕЛЬ САМОСОГЛАСОВАННОГО ПОЛЯ РЕАКЦИИ

В рамках макроскопической теории (шарик с фиксированным распределением зарядов погружен в среду с диэлектрической про­ницаемостью ε, заряды локализованы внутри шарика) энергия взаи­модействия с растворителем задается электростатическим класси­ческим потенциалом

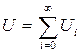, где U₀=(q²/2α)(1– 1/ε); U₁=(μ²/2α³)[2(ε – 1)/(2ε + 1)]

и т.д. Здесь q, μ и α - заряд, дипольный момент и радиус шарика соответственно. Первый член этого ряда называют борновским, вто­рой - онзагеровским. Следующие члены ряда зависят от квадрупольного и более высоких мультипольных моментов шарика. Для электрически нейтральных шариков U_o=0 и первым ненулевым членом ряда будет U₁. В работах Тапиа с сотр. [88 - 92] предложено добавить аналог члена U₁ к гамильтониану изолированной моле­кулы и учесть таким способом взаимодействие с растворителем. В результате ими было получено следующее выражение для вычисления гамильтониана молекулы, находящейся в растворителе:

Ĥ=Ĥ₀ -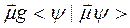

где g - тензор, который определяется восприимчивостью электро­статического поля молекулы средой. В работах [88 - 92] он задавался в параметрической форме.

Этот метод учета взаимодействия с растворителем получил наз­вание модели самосогласованного поля реакции. Основные его не­достатки очевидны. Они заключаются в необходимости учета зави­симости тензора g от значения диэлектрической проницаемости растворителя и размеров молекулы. Это нельзя сделать без очень грубых дополнительных предложений. Обычно полагают, что диа­гональные элементы g равны 2(ε - 1)/[(2ε + 1)α³], а недиагональные - нулю. Однако перенесение макроскопической формулы на микроскопи­ческий уровень, вообще говоря, неверно, диэлектрическая прони­цаемость при этом теряет свой физический смысл, а выбор значения параметра α (радиуса молекулы) достаточно произволен. Поэтому модель самосогласованного поля реакции имеет ограниченную область применения. Практически ею можно пользоваться при рассмотре­нии реакций изомеризации и переноса протона. В остальных случаях ее использование нежелательно.

2.4. ПРИБЛИЖЕНИЕ СУПЕРМОЛЕКУЛЫ

С точки зрения построения модели наиболее простым спосо­бом учета сольватации является включение большого числа моле­кул среды в систему, для которой проводится квантовохимический расчет. Все ее электроны (сольватируемой молекулы и молекул среды) включаются в электронный гамильтониан. Этот способ явля­ется непосредственным обобщением квантовохимических методов, развитых для отдельных молекул на случай больших систем, состоя­щих из нескольких или даже большого числа отдельных молекул. Если нам удастся учесть таким способом взаимодействие растворен­ной молекулы с большим числом молекул cреды, рассчитать энерге­тически наиболее выгодную конформацию растворенной молекулы и конфигурацию молекул растворителя и получить для этой конфигурации электронную волновую функцию, то мы сможем объяснить или даже предсказать практически все интересующие нас свойства молекулы в растворе. При этом следует с особой осторожностью подходить к выбору квантовохимического метода, к которому в этом случае предъявляются повышенные требования, а именно он должен быть пригоден для изучения межмолекулярных взаимодействий.

Из предыдущей главы было видно, что многие квантовохимические методы, которые успешно используются для изучения реак­ционной способности органических соединений дают неправильные результаты при расчете параметров, характеризующих межмолекуляр­ные взаимодействия. Например, метод МПДП дает неудовлетворительные результаты при расчете систем с водородными связями. Поэто­му при использовании приближения "супермолекулы" для учета сольватации приходится выбирать достаточно совершенный квантовохимический метод. При этом возникают трудности, связанные с очень большим размером супермолекулы, которая состоит из растворенного соединения и молекул среды. Кроме того, в супермолекуле обычно неизвестно большое число геометрических параметров, которые опре­деляют строение сольватационной оболочки. Поэтому выполнить реаль­но такие расчеты удается только для систем с небольшим числом молекул среды.

Такой учет сольватации, при котором система из сольватируемой молекулы и некоторого ограниченного числа молекул раст­ворителя рассчитывается квантовохимическим методом как одна молекула, получил название "приближения супермолекулы" [93, 94]. Расчеты в этом приближении широко распространены. К ним от­носятся работы, в которых вычисляются параметры для комплек­сов, состоящих из растворенной молекулы и одной молекулы раст­ворителя, а также расчеты для комплексов с двумя, тремя и т.д. молекулами среды. В этих работах впервые удалось получить данные о строении и энергии взаимодействия для гидратных обо­лочек ионов ОН^- и Н₃О⁺ [65]. Несколько позже аналогичными методами исследованы гидратационные оболочки простейших ионов: Li⁺, Be²⁺, Na⁺, Mg²⁺, Al³⁺, К⁺, Ca²⁺, F^-, Сl^-, NH₄⁺ [95 - 102], CH₅⁺, CH₅^- [103], алкиламмониевых ионов [104].

Методика проведения перечисленных выше работ заложила осно­ву подхода к изучению сольватации в приближении супермолеку­лы. Суть этих подходов заключается в следующем. Вначале рас­считывается энергия взаимодействия иона с одной молекулой воды и определяется наиболее энергетически выгодная конформация, по­том в систему добавляется еще одна молекула воды и вновь рассчитываются энергия взаимодействия и структура комплекса и т.д. В результате такого расчета получается набор величин, ко­торые являются энергиями гидратации иона А каждой последующей молекулой воды (E_n,n-1):

А•(n - 1)Н₂O + Н₂O → А•nН₂O + E_n,n-1.

Для простейших ионов эти энергии были сопоставлены с экспе­риментальными данными, полученными методами масс-спектрометрии высоких давлений и циклотронного резонанса. Хорошее согласие с экспериментом подтвердило широкие возможности квантовохимических расчетов для изучения сольватации. Кроме того, были по­лучены данные о числе молекул воды в первой гидратационной сфере и их конфигурация.

При переходе к более сложным молекулам расчеты в прибли­жении супермолекулы существенно усложняются, так как центров сольватации уже много и заполнить даже всю первую гидратационную оболочку практически не удается. Поэтому в большинстве работ придерживаются следующей последовательности:

1) детально изучается взаимодействие сольватируемой молекулы с одной молекулой растворителя и получается предварительное представление о строении сольватационной оболочки;

2) изучается влияние второй, третьей и т.д. молекул раство­рителя на строение сольватационной оболочки и уточняются данные, полученные на первом этапе;

3) в изучаемую систему вводится максимально возможное ко­личество молекул растворителя, для которого удается выполнить расчет, и для такой супермолекулы вычисляются все интересующие величины.

Детальное изучение взаимодействия сольватируемого соединения и одной молекулы растворителя включает их сближение (с различ­ной взаимной ориентацией) и вращение вокруг собственных ло­кальных осей. На этом этапе получают данные об основных наи­более выгодных положениях молекул растворителя, энергиях взаи­модействия в таких положениях, расстояниях между растворен­ным соединением и молекулами растворителя и о подвижности последних. Обычно различают три вида подвижности: в положении равновесия, вблизи положения равновесия и вдали от положения равновесия.

Подвижность в положении равновесия — возможность молекулы растворителя вращаться вокруг собственных локальных осей. Для изучения этого вида подвижности рассчитывают зависимость энер­гии взаимодействия растворенного соединения и молекулы раст­ворителя от углов поворота последней вокруг ее локальных осей. Расстояние между ними при этом не меняется. Подвижность вблизи положения равновесия — возможность мо­лекулы растворителя смещаться на небольшие расстояния от по­ложения равновесия. Для изучения этого вида подвижности рассчи­тывают форму ППЭ при небольших удалениях молекулы раст­ворителя от положения равновесия без разрыва водородных свя­зей, которые были в положении равновесия. Подвижность вдали от положения равновесия — возможность молекулы растворителя смещаться на большие расстояния от по­ложения равновесия. Для изучения этого вида подвижности рас­считывают ППЭ при больших удалениях молекулы растворителя от положения равновесия, когда водородные связи между ней и растворенным соединением разорваны.

На втором этапе увеличивают число молекул растворителя в супермолекуле. При этом используют данные о положениях ло­кальных минимумов, полученные на первом этапе, и лишь уточ­няют их положение. На третьем этапе в супермолекулу включают максимально воз­можное количество молекул растворителя (исходя из возможностей ЭВМ) и проводят расчет того или иного параметра.

В качестве примера рассмотрим результаты работы [105], в ко­торой изучено строение гидратационной оболочки мочевины. Это соединение обладает рядом уникальных свойств. Так, в его при­сутствии резко снижается температура, при которой в водных растворах происходит денатурация белков и других биополимеров, повышается растворимость неэлектролитов и т.д. Принято гово­рить, что в присутствии мочевины разрушаются водородные связи между молекулами воды, другими словами, молекулы воды в вод­ном растворе становятся более подвижными. Это приводит к пере­численным выше химическим и биохимическим эффектам. Однако механизм этого явления на микроскопическом уровне установлен не был. Для решения этого вопроса было изучено [105] строение гидратационной оболочки мочевины с помощью квантовохимических расчетов методами ППДП/2 и ОСТ-ЗГФ.

На первом этапе был проведен расчет строения комплекса, образованного одной молекулой мочевины с одной молекулой во­ды, и рассмотрена подвижность последней в этом комплексе. Ока­залось, что наиболее устойчивый комплекс имеет следующую кон­фигурацию:

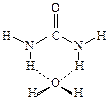
В этом комплексе молекула воды связана двумя водородными связями с двумя атомами Н связей N—Н, которые находятся в транс-положении по отношению к карбонильной группе. Расчет также показал, что в этом положении молекула воды обладает необычайно высокой подвижностью. Она может смещаться на рас­стояния до 0,15—0,20 нм от положения равновесия, и при этом энергия взаимодействия в комплексе почти не меняется. Таким образом, было обнаружено, что в исследованном комплексе мо­лекулы воды и мочевины частично сохраняют свободу независимых перемещений в пространстве.

На втором этапе было увеличено количество молекул воды в комплексе, однако оказалось, что вторая молекула Н₂О не может связаться с молекулой мочевины аналогично первой и образовать комплекс типа

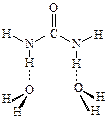
Таким образом, первая молекула воды, присоединяясь к моче­вине, попадает в широкую потенциальную яму (именно этим объяс­няется ее высокая подвижность), но вторая молекула воды в эту потенциальную яму попасть не может, поэтому при увеличении количества молекул воды в комплексе высокая подвижность одной из них сохраняется. По-видимому, наличие этой достаточно ши­рокой и глубокой потенциальной ямы обусловливает способность мочевины "разрушать структуру воды".

Введение мочевины в воду приводит к тому, что часть мо­лекул воды, которые в чистом водном растворе (без мочевины) образовывали упорядоченную структуру (за счет образования во­дородных связей между собой), попадают в широкую потенциаль­ную яму, созданную мочевиной. Такие молекулы не занимают оп­ределенного положения в пространстве и сохраняют способность перемещаться на большие расстояния (в пределах размеров по­тенциальной ямы). Поэтому как сами эти молекулы, так и моле­кулы воды из их непосредственного окружения не могут участво­вать в образовании упорядоченной структуры воды. Подвижность молекул воды в данном случае увеличивается. Происходит как бы локальное повышение термодинамической температуры. Однако в действительности этот эффект обусловлен не повышением энергии молекулы воды, локализованной на ее вращательных и поступа­тельных степенях свободы, а снижением потенциальных барьеров на пути ее перемещения.

Таким образом, предложен [105] механизм повышения термо­динамической температуры водных растворов при добавлении в них мочевины. Квантовохимические расчеты помогли его найти, но сами по себе они не могут служить доказательством, что экспериментально наблюдаемые эффекты происходят именно по такому механизму. Для этого необходимо на основе предложен­ного механизма сделать предсказания, которые можно проверить экспериментально. Такие предсказания были сделаны [105]. Они ка­сались влияния алкильных заместителей на способность мочевины повышать термодинамическую температуру водных растворов.

У метилмочевины наиболее устойчивой является следующая конформация:

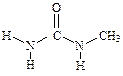
Наличие двух связей N—Н в транс-положении по отношению к карбонильной группе ведет к сохранению особенностей строения комплекса, описанных выше. Поэтому у метилмочевины сохраняется способность повышать термодинамическую температуру воды.

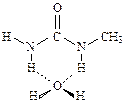
У диметилмочевины возможны два изомера

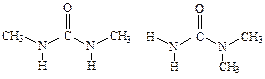
У первого из них две связи N—Н в транс-положении по отношению к карбонильной группе, а у второго - лишь одна. Следователь­но, первый изомер будет повышать термодинамическую темпе­ратуру воды и приводить к тем же эффектам, что и мочевина, а второй - нет. Это теоретическое предсказание получило экспе­риментальное подтверждение.

Приближение супермолекулы позволяет решать многие задачи, связанные с влиянием сольватации на реакционную способность органических соединений. Однако при его использовании необходи­мо самое серьезное внимание уделить выбору метода расчета. При этом следует руководствоваться двумя требованиями: 1) ме­тод расчета должен быть достаточно точным и хорошо передавать как основные свойства растворенной молекулы, так и строение сольватационных оболочек; 2) расчет в приближении супермолеку­лы связан с вычислением электронной волновой функции для очень большой системы, и он должен быть практически реализуем исхо­дя из возможностей имеющихся ЭВМ, их быстродействия и памяти. До недавнего времени расчеты с учетом сольватации в приближе­нии супермолекулы проводились методами ППДП/2 и ОСТ-ЗГФ. Именно эти методы были использованы в приведенном выше при­мере изучения особенностей строения гидратационной оболочки мо­чевины. В настоящее время предпочтительнее использовать метод МПДП/Н и неэмпирические расчеты в базисе 3-21ГФ.

2.5. МЕТОД АТОМ-АТОМНЫХ ПОТЕНЦИАЛОВ

В приближении супермолекулы мы рассматривали систему из сольватированного соединения и некоторого числа молекул раство­рителя как одну большую молекулу. Такой подход является не­посредственным обобщением методов квантовой химии, разрабо­танных для расчета свойств отдельных (изолированных) соедине­ний на межмолекулярные взаимодействия. При этом в качестве исходных частиц приходится оперировать электронами и атом­ными ядрами. При изучении системы, состоящей из одной молекулы, такой подход является единственно возможным, так как только на этом уровне можно анализировать большинство химических свойств молекулы. При рассмотрении межмолекулярных взаимо­действий появляется возможность оперировать не с электронами и атомными ядрами, а с отдельными молекулами. Для этого не­обходимо иметь потенциалы, описывающие межмолекулярные взаимодействия. В случае системы, состоящей из электронов и ядер, необ­ходимо решать уравнение Шредингера, так как электроны следует рассматривать как квантовые частицы. При рассмотрении межмо­лекулярных взаимодействий молекулы можно рассматривать как классические объекты. Благодаря этому появляется возможность использовать для их описания эмпирические потенциальные функции. Это существенно упрощает задачу.

Различные эмпирические потенциалы, которые предлагались раз­личными авторами для описания межмолекулярных взаимодействий, не удовлетворяют точности, необходимой при учете сольватации. Отсутствие достаточно надежных потенциалов делало невозможным использование такого подхода для изучения сольватации. Сущест­венный прогресс в этой области был достигнут благодаря работам Клементи с сотрудниками. Ими была выдвинута идея использовать неэмпирические квантовохимические расчеты для определения потен­циалов межмолекулярных взаимодействий [106—109]. Первоначально потенциалы генерировались в численной форме путем неэмпирического расчета энергии взаимодействия сольватированной молекулы и моле­кулы растворителя. Но, так как дальнейшее использование числен­ного потенциала для построения сольватационной оболочки затруд­нительно, была подобрана аналитическая функция для его аппрокси­мации, которая представляла собой сумму атом-атомных потенциалов. При этом все атомы в молекуле были разбиты на классы в зависимости от того, к каким функциональным группам и в каких положениях в группах находится данный атом. В результате число классов во много раз превышало число различных атомов. Для атомов каж­дого класса подбирались свои атом-атомные потенциалы. Аналити­ческая форма, в которой производился поиск атом-атомных по­тенциалов, выбиралась разной и зависела от базиса, использован­ного в расчете. При вычислении потенциала взаимодействия между молекулами в небольших базисах обычно использовалась относи­тельно простая аналитическая функция

U_ij = -A_ij/r⁶_ij + B_ij/r¹²_ij + C_ijq_iq_j/r_ij

где U_ij - энергия взаимодействия между атомами i и j; r_ij - расстояние между этими атомами; q_i и q_j - заряды на атомах; А_ij, В_ij и С_ij - эмпирические параметры, зависящие от того, к каким классам при­надлежат атомы i и j.

Для нахождения потенциалов межмолекулярных взаимодействий неэмпирическими методами с использованием больших базисов, близ­ких к хартри-фоковскому пределу, использовались более сложные аналитические функции. Расчеты в больших базисах были про­ведены для определения аналитических потенциалов, описывающих взаимодействие между молекулами воды. Расчеты в минимальном базисе были использованы для определения атом-атомных потен­циалов, описывающих взаимодействие между молекулой воды и осно­ваниями ДНК, аминокислотами и т.д.

Число классов атомов у молекул типа оснований ДНК и амино­кислот составляет несколько десятков, число неизвестных параметров в атом-атомных потенциалах достигает нескольких сотен. При определении значений этих параметров приходится варьировать относительное положение и взаимную ориентацию молекул в доста­точно широких пределах, практически для вычисления каждого пара­метра приходится делать 15 - 20 расчетов. Таким образом, для рас­чета потенциала межмолекулярного взаимодействия молекул среднего размера типа оснований ДНК и молекул воды необходимо сделать не­сколько десятков тысяч расчетов полной энергии системы неэм­пирическим методом. Поэтому процедура подбора параметров свя­зана с очень большими затратами машинного времени. Но следует отметить одно благоприятное обстоятельство: по мере накопле­ния наборов параметров и создания их банка для каждого нового соединения объем вычислений сокращается, так как оказывается возможным отнести большинство атомов к уже известным классам, для которых все параметры аналитических потенциалов известны из расчетов других молекул [110].

После нахождения потенциалов расчет строения сольватационной оболочки и энергии взаимодействия между растворителем и растворенным соединением становится относительно простой зада­чей, аналогичной задачам конформационного анализа. Аналитическая форма, в которой в настоящее время найдены потенциалы для описания взаимодействия молекул среднего размера и молекул воды, также совпадает с наиболее широко распространенными по­тенциалами, которые используются в конформационных расчетах. Однако параметры в потенциалах Клементи для межмолекулярных взаимодействий имеют совершенно иную природу. В конформационном анализе потенциалы типа 6 - 12 описывают ван-дер-ваальсовы взаимодействия между атомами, а у Клементи - электронодонорные и электроноакцепторные взаимодействия. Третий член в фор­муле для атом-атомных потенциалов соответствует кулоновскому взаимодействию. Для электрически нейтральных молекул значение коэффициента С_ij в потенциалах Клементи близко к единице. Од­нако для ионов оно не превышает 0,5; это связано, по-видимому, с эффектами экранирования и перераспределения заряда.

Использование потенциалов Клементи позволяет рассматривать гидратацию весьма сложных молекул большим числом молекул воды. Пока число молекул воды не превышает 10 - 15, каких-либо сущест­венных трудностей при расчете строения гидратационной оболоч­ки не возникает. Однако при дальнейшем увеличении числа мо­лекул воды появляется ряд новых проблем. Для достаточно точ­ного описания гидратационной оболочки даже небольшого соеди­нения количество молекул воды желательно увеличить до 200 - 300. При расчете строения такой огромной гидратационной оболочки основная трудность заключается в существовании большого числа структур с близкими энергиями. Задача сводится к нахождению всех таких структур, определению вероятности реализации каждой из них и усреднению по всем найденным структурам. В таком расчете приходится учитывать температурную зависимость.

В работах Клементи показано, что для нахождения строения гидратационных оболочек можно успешно использовать метод Мон­те-Карло, с помощью которого были проведены расчеты строения гидратационных оболочек ряда простых ионов с учетом их взаимо­действия с 200 - 250 молекулами воды. При этом возникла еще одна проблема. Распределение молекул воды в расчетах методом Монте-Карло носит вероятностный характер, поэтому перед исследователя­ми встала задача перехода к таким простым и наглядным характе­ристикам гидратации, как число молекул воды в первой гидратацион­ной сфере и ее радиус. Для получения этой информации было пред­ложено вычислить зависимость плотности атомов водорода или кислорода от расстояния до центра иона. На таких графиках по­лучается ряд четко выраженных максимумов. Их положение для атомов кислорода обычно связывают с радиусами гидратацион­ных оболочек, а площадь под кривыми - с количеством молекул воды в оболочке. Ниже приведены радиусы первых гидратацион­ных оболочек (R) и число молекул воды в них (N), вычисленные таким способом [108, 109].

Ион	R, нм	N
Li+	0,19—0,20
Na+	0,23—0,24	5—6
К+	0,28—0,29	5—7
F-	0,27—0,28	4—6
Cl-	0,34—0,35	6—7

Использование атом-атомных потенциалов весьма перспективно и может существенно расширить наши представления о сольватации и ее влиянии на реакционную способность органических соедине­ний. Банк параметров в настоящее время достаточно велик, и можно надеяться, что в будущем он будет еще расширен. Однако следует подчеркнуть те допущения, которые делаются в этих рас­четах.

1. Используется приближенный квантовохимический метод (для молекул среднего размера весьма грубый) для вычисления пара­метров атом-атомных потенциалов. В случае небольшого числа молекул растворителя ошибки могут быть невелики, но по мере увеличения их количества они будут накапливаться.

2. Ошибки в расчетах могут возникать за счет аппроксима­ции численного потенциала весьма простыми аналитическими функ­циями.