Фермой с составными, или сложными элементами
Фермой с составными, или сложными элементами, называют такую ферму, в которой ряд прямолинейных стержней заменен составными стержням в виде фермочек. В ферме изображенной на рис. 1.4.6, а, вместо простых элементов по нижнему поясу даны сложные элементы Оа, аb, bf
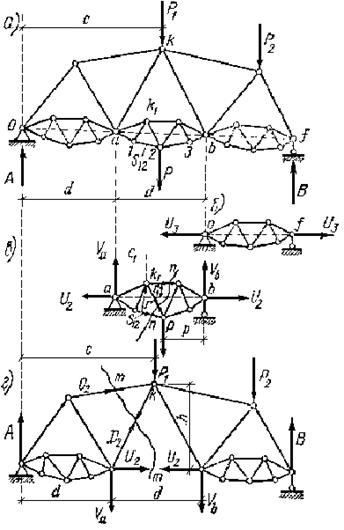
Рисунок 1.4.6
Заменяя составные стержни прямолинейными, получаем первоначальную, так называемую основную ферму, из которой образована ферма с составными элементами. Узлы составной фермы называют главными; узлы, расположенные между главными, дополнительными. При отсутствии составных элементов и том же приложении нагрузки стержень основной фермы аb испытывал бы кроме действия осевой силы еще поперечный изгиб от силы Р.
Рассматриваем два случая действия нагрузки:
1) нагрузка не приложена в дополнительных узлах данного сложного элемента;
2) нагрузка имеется и в промежуточном узле фермочки.
В первом случае (элемент bf на рис.1.4.6 б), выделяя фермочку разрезами у главных узлов, получаем из условия равновесия фермочки, что по концам ее со стороны главных узлов будут воздействовать только осевые силы U3 направленные по прямой, соединяющей главные узлы. Эти осевые силы легко определить способом, известным для простых ферм.
Рассмотрим теперь определение усилия S12 в стерженьке составного элемента ab к промежуточному узлу 2 которого приложена вертикальная нагрузка Р (рис. 1.4.6, а). Выделим этот элемент из фермы разрезами у узлов а и b (рис.1.4.6, в). Реакции со стороны узлов а и b представляем каждую в виде двух составляющих Va, U2 и Vb, U2 из которых составляющие U2 направлены по оси составного элемента, т.е. по линии аb.
Из условия равновесия фермочки 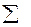 Х = 0 получаем, что правая горизонтальная реакция U2 равна по величине и противоположна по направлению левой реакции U2; найти же величину U2 из условия равновесия фермочки невозможно. Вертикальные реакции фермочки легко находятся. Составляя условие равновесия в виде суммы моментов относительно точки b:
Х = 0 получаем, что правая горизонтальная реакция U2 равна по величине и противоположна по направлению левой реакции U2; найти же величину U2 из условия равновесия фермочки невозможно. Вертикальные реакции фермочки легко находятся. Составляя условие равновесия в виде суммы моментов относительно точки b:
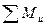 =0
=0
получаем: Vad – Pp =0
откуда Va = Pp/d (а)
Составляя условие равновесия в виде суммы моментов относительно точки а, получаем
-Vb d + P (d – p) =0
откуда Vb= P (d – p) / d (б)
Вертикальные реакции Va и Vb малой фермочки от местной нагрузки находят так же, как реакции простой балки с пролетом l = d. Можно считать фермочку аb опертой статически определимо на главные узлы. Усилия в стерженьках этой фермочки можно найти, зная все внешние силы для нее, в том числе и осевые силы U2.
Для определения осевых сил рассмотрим равновесие части всей фермы (рис. 1.4.6, г). Выделив сложный элемент аb из заданной фермы, возмещаем его связи в а и b опорными давлениями Va и Vb и осевыми силами U2 направленными от узлов. Опорные давления Va и Vb по величине равны вертикальным опорным реакциям фермочки и определяются формулами (а) и (б). Рассекая ферму разрезом м—м и рассматривая равновесие левой ее части, составляем условие равновесия:
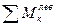 =0
=0
или в развернутом виде Ас - Va (с—d)- U2h = 0
откуда U2 = [Ас - Va (с—d)]/h =М 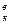 / h (в)
/ h (в)
где М 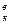 - момент левых вертикальных сил относительно точки к. Выражение (в) показывает, что осевая сила сложного элемента вычисляется так же, как в элементе простой фермы, но особенностью является разложение промежуточной нагрузки на составляющие Va и Vb приложенные к главным узлам.
- момент левых вертикальных сил относительно точки к. Выражение (в) показывает, что осевая сила сложного элемента вычисляется так же, как в элементе простой фермы, но особенностью является разложение промежуточной нагрузки на составляющие Va и Vb приложенные к главным узлам.
После определения осевой силы U2 возвращаемся к рассмотрению фермочки аb (рис. 1.4.6, в). Найдем усилие во втором элементе нижнего пояса фермочки S12. Для этого проводим разрез п—п и рассматриваем равновесие левой части фермочки:
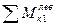 =0
=0
или Vac1 +U2 r 1 –S12r= 0,
откуда S12 = Vac1/r +U2 r 1/r (г)
Первый член правой части представляет собой усилие в стерженьке 1—2 составного элемента от местной вертикальной нагрузки; назовем его S12мес. Второй член правой части можно рассматривать как усилие в том же стерженьке 1—2 от осевых сил U2 обозначим второй член S12ос. Получаем следующее общее выражение для полного усилия в любом стержне фермочки:
S12= S12мес + S12ос
где в данном случае: S12мес= Vac1/r ;
S12ос= U2 r 1/r
Усилие от местной нагрузки возникает только тогда, когда нагружен данный сложный элемент, и это воздействие называют потому местным. Усилие от осевых сил может быть равно осевой силе, если r = r 1.
Различают для ферм с составными элементами четыре категории стержней (рис 1.4.7):
- стержни первой категории, в которых возникают усилия только от осевых сил (стержни основной фермы, например 6—7, 6—8, 6—5, 6—3);
-стержни второй категории, которые получают усилии только от местной вертикальной нагрузки и входят лишь в состав шпренгеля (стерженьки 3—1, 3—4, 4—5, 1—4, 4—2, 2—5);
- стержни третьей категории, которые входят в состав основной фермы и в состав малой фермочки, причем усилия в таких стержнях определяют по общей формуле (г) путем суммирования усилий от осевых сил и от местной вертикальной нагрузки(а—1, 1—2, 2—b, а—З, b—5);
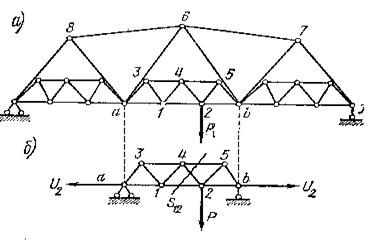
Рисунок 1.4.7
В фермах, в которых шпренгели меняют характер воздействия груза на главные узлы и меняются усилия в стойках основной фермы, то такие стойки относят к стержням четвертой категории.
