Расчет рН сильных кислот и оснований

Задача.

В реакции А ® В + С с общим порядком, равным единице, константа скорости k₁ = 5×10^-5 с^-1. Определите концентрацию веществ А и В и скорость реакции через 1 час и через 5 часов, если начальная концентрация А составляла 0,2 моль/л.

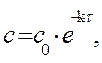Решение. Для реакции 1-го порядка справедливо уравнение

где с – текущая концентрация вещества в момент времени

τ, с₀ – начальная концентрация, k – константа скорости, τ – время.

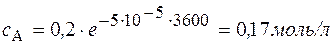
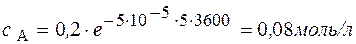Через 1 час

Через 5 часов

Концентрация вещества В находится по стехиометрическому соотно­шению веществ А и В. Из уравнения реакции следует, что концентрация вещества В возрастает на ту же величину, на какую убывает концентрация А, т. к. из 1 моль А получается 1 моль В.

Поэтому через 1 час

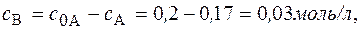
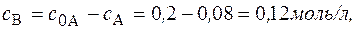Через 5 часов

Рассчитаем скорость реакции по уравнению: υ = k×с_А

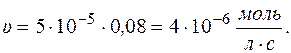
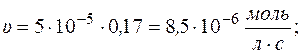Через 1 час

Через 5 часов

Задача. Для реакции первого порядка А ® 2В определите время, за которое прореагирует 90 % вещества А. Константа скорости реакции k₁ = 10^-4 с^-1.

Решение. После превращения 90 % вещества А его концентрация соста­вит 10% от начальной концентрации, т. е. 0,1 с_0.

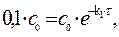
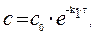Из уравнения получим, что

Þ τ = ln 10/k₁ = 23026 с = 6,4 ч.

Задача. При изучении кинетики термического разложения ацетона, являющегося реакцией первого порядка, в соответствии с уравнением:

СН₃СОСН₃(г) ® С₂Н₄(г) + СО(г) + Н₂(г)

получены следующие экспериментальные данные при Т = 802 К: давление в реакторе изменилось от начального р₀ = 312 мм. рт. ст. до 408 мм. рт. ст. за 390 с. Рассчитайте константу скорости реакции.

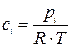Решение. Все вещества в системе находятся в газообразном состоянии, и, учитывая условия проведения опыта, предполагаем, что они подчиняются законам идеальных газов. Следовательно, концентрация и парциальное давление газа связаны зависимостью

p_i=c_i×R×T или

Þ для реакции I-го порядка

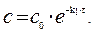
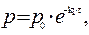
Если р₀ – это начальное давление ацетона в реакционном сосуде, то для решения задачи необходимо определить парциальное давление этого веще­ства к моменту времени, когда общее давление

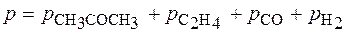составило 408 мм. рт. ст.

Из стехиометрии реакции видно, что 1 моль ацетона, распадаясь, обра­зует 3 моль газа. Из закона Авогадро следует, что при уменьшении парци­ального давления ацетона на Dр сумма парциальных давлений образовав­шихся газов составит 3Dр. Таким образом, можно записать

P = p₀ – Dp + 3×Dp

или

408 = 312 + 2×Dp, Dp = 48 мм рт.ст.

Следовательно, парциальное давление ацетона через 390 с после начала опыта составило 312 – 48 = 264 (мм. рт. ст.).

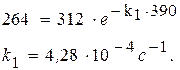После подстановки в уравнение получим:

Задача.При температуре 100 °С константа скорости реакции второго порядка

2НI(г) ® Н₂(г) + I₂(г)

равна 8,83×10^-16 л/(моль×с). Определите время полупревращения йоди­стого водорода, если начальная концентрация его равна 1 моль/л.

Решение. Для реакции с n = 2:

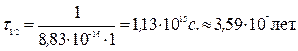
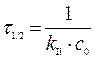Задача. В реакции второго порядка А + В ® D за 1 час концентрации веществ А и В уменьшились по сравнению с начальной с_0А = с_0В = 0,2 моль/л на 30 %. Определите константу скорости и скорость реакции в начальный момент времени и через час после начала реакции.

Решение. Концентрации веществ А и В за 1 час уменьшились на

0,3×с₀ = 0,06 моль/л. Отсюда, через час концентрации составят

с_А = с_В = 0,2 – 0,06 = 0,14 (моль/л).

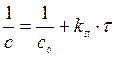Для реакции II-го порядка

Þ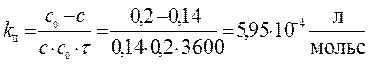

υ₀ = k_II• c_0A• c_0B = 5,95∙ 10^-4∙0,2∙0,2 = 1,38∙ 10^-5 моль/(л∙с)

Через 1 час:

υ = k_II• c_A• c_B = 5,95∙ 10^-4∙0,14∙0,14 = 1,16∙ 10^-5 моль/(л∙с)

ЗАДАЧА. Рассчитайте изменение константы скорости реакции, имеющей энергию активации 191 кДж/моль, при увеличении температуры от 330 до 400 К.

Решение. Зависимость константы скорости реакции от температуры опре­деляется уравнением Аррениуса

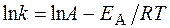
или

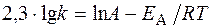
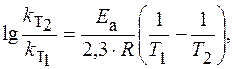Логарифм отношения констант скоростей реакции при температурах Т₂ и Т₁ соответственно равен

где R = 8,31 Дж/(моль×К).

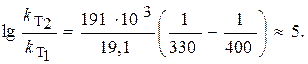Подставив в это уравнение данные задачи, получим

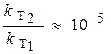
Вывод: при увеличении температуры на 70 К скорость реакции возросла в 100000 раз (!)

ПРИМЕР. Имеется раствор H₃PO₄ с массовой долей w = 30% и плотностью r = 1,18 г/см³. Вычислите с_{М ,} с_{эк ,} Т, c_m и χ H₃PO₄ в этом растворе.

Молярность - ?

Масса 1л раствора равна:

m_р-ра= r_р-раV_р-ра = 1,18×1000 = 1180 г.

В 1 л р-ра:

m(H₃PO₄) = (m_р-ра ∙ w)/100% = (1180×30)/100 = 354 г.

M(H₃PO₄) = 98 г/моль.

v( H₃PO₄)= m(H₃PO₄)/M(H₃PO₄) =354/98 = 3,61 моль.

Þ с_М = 3,61 моль/л, (3,61 М H₃PO₄).

Нормальность -?

Э(H₃PO₄) =1/3 H₃PО₄, f_э (H₃PO₄) = 1/3

в 1 моле H₃PО₄ содержится 3 моль-эквивалента

Þ в 1 л раствора 3,61×3 = 10,83 моль -экв Н₃РО₄.

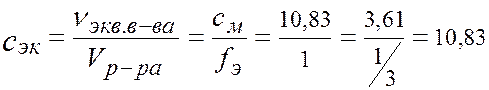моль/л

с_эк = 10,83 моль/л, (10,83 н H₃PO₄).

Титр -?

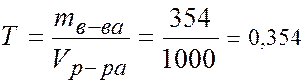г/мл

Т= 0,354г/мл/

Моляльность - ?

В 100 г раствора: 30 г Н₃РО₄ и 70 г Н₂О.

В 1000 г Н₂О:

m (H₃PO₄)= (1000×30)/70 = 428,5 г.

v(H₃PO₄) = m(H₃PO₄)/M(H₃PO₄) = 428,5/98 = 4,37 моля.

Þ с_m = 4,37 моль/1000 г Н₂О.

Молярная доля - ?

В 1л раствора:

m(H₂O) = 1180 – 354 =826 г.

v(H₂O) = m(H₂O)/M(H₂O) = 826/18 = 45,89 молей.

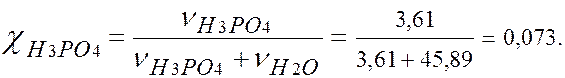
χ (H₃PO₄ ) = 0,073.

ЗАДАЧА

Р _н.п. чистого ацетона(СО(СН₃)₂) при 20º С равно 23940 Па.

Р _н.п. ацетона над раствором, содержащем 5 г камфоры на 200 г ацетона, при той же Т равно 23710 Па. Определите молекулярную массу камфоры.

Решение.

М (ацетона) = 58 г/моль. М камфоры – х г/моль.

Согласно закону Рауля:

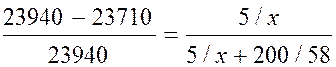, откуда х = 151 г/моль.

ЗАДАЧА

Вычислите Т_кип и Т_зам водного раствора глицерина с массовой долей С₃Н₈О, равной 5%. M(С₃Н₈О) = 92 г/моль.

Решение

В 100 г раствора: 5 г С₃Н₈О и 95 г Н₂О.

В 1000 г Н₂О:

m (С₃Н₈О)= (1000×5)/95 = 52,6 г.

v(С₃Н₈О) = m(С₃Н₈О)/M(С₃Н₈О) = 52,6/92 = 0,57 моля.

Þ с_m = 0,57 моль/1000 г Н₂О.

Используя закон Рауля и справочные значения К_э и К_к для воды, находим:

ΔТ_зам = 1,86 · 0,57 = 1,06º, ΔТ_к = 0,52 · 0,57 = 0,29º,

Þ Т_з = -1,06º С, Т_к = 100,29º С.

ЗАДАЧА. При 18 ºС осмотическое давление раствора глицерина равно 3,039 · 10⁵ Па. Каково будет Р осм, если раствор разбавить в 3 раза, а Т повысить до 37 º С?

Решение.

В соответствие с уравнением Вант-Гоффа:

· концентрация раствора С₁ до разбавления: .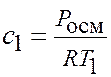

· осмотическое давление раствора Р'_осм. после разбавления и повышения Т:

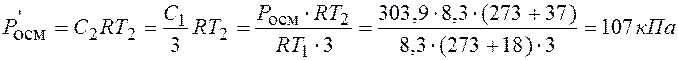
ПРИМЕР

Оцените степень диссоциации a по 1-й ступени в 0,005 М и 0,05 М растворах сернистой кислоты Н₂SО₃.

Решение.

Н₂SО₃ 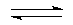Н⁺ + НSО₃^-, К_Д1 = 1,7×10 ^-2 (1-я ступень)

! значение К_Д1 относительно велико (> 10^-4) Þ

расчет a по строгой формуле Оствальда:

К_Д = a²с₀/(1 - a).

·

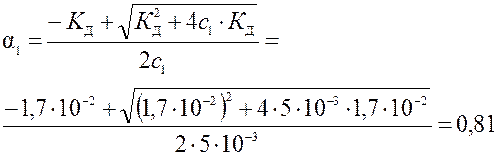Для 0,005 М раствора:

! Расчет по приближенной формуле (К_Д » a²с₀) приводит к величине a > 1, что не имеет смысла.

· Для 0,05 М раствора

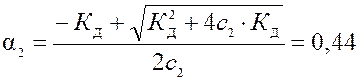Значение a, рассчитанное по при­ближенной формуле (» 0,58) сильно отличается и неверно!

a - уменьшается с ↑ концентрации

ПРИМЕР.

Рассчитайте активность ионов в 0,01 М растворе СаСl₂.

СаCl₂ ® Ca²⁺ + 2Cl^-

С, моль/л: 0,01 0,012×0,01

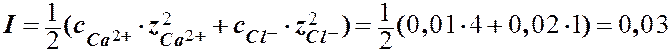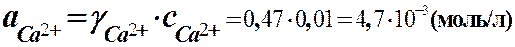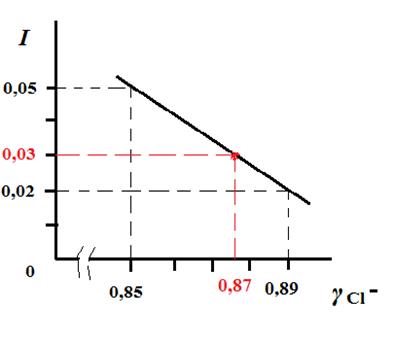
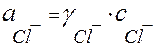= 0,87×0,02 = 1,74×10^-2 (моль/л)

Расчет рН сильных кислот и оснований

а) для кислот:

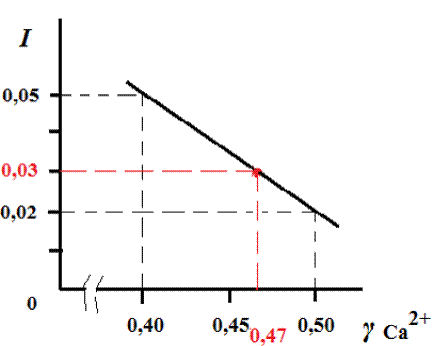
I_р-ра = 0,5 × å(с_i × z²_i ) Þ g_Н⁺ (по таблице или формуле)

Þ а_Н⁺ = g_Н⁺ × с_Н⁺ Þ рН = -lg а_Н⁺

б) для оснований:

I_р-ра= 0,5 × å(с_i × z²_i ) Þg_OН^- (по таблице или формуле)Þ а_ОН^- = g_ОН^-× с_ОН^-Þ рН = 14 + lg а_ОН^-

рН = 14 - рОН =14 + lg а_ОН^- = 14 + lg g_ОН^-.с_ОН^-

ЗАДАЧА

Рассчитайте рН 0,05 М раствора НСN.

Решение.

НСN 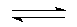Н⁺ + СN^-

слабая кислота, с_о = 0,05 моль/л, К_Д= 7,9×10^-10 (из таблицы)

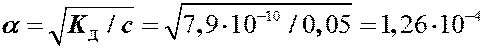a < 0,07 Þ расчет по упрощенной формуле:

с_H⁺ = aс_о = 1,26×10^-4×0,05 = 6,3×10^-6 моль/л

рН = ‑lg с_H⁺ = - lg 6,3×10^-6 = 5,18.

ЗАДАЧА

Рассчитайте концентрацию азотистой кислоты НNО₂ в растворе с рН = 2,7.

Решение.

НNО₂ Н⁺ + NО₂^-.

слабый электролит, К_Д= 4,6×10^-4

рН = 2,7 Þ при равновесии

[H⁺] = [NO₂ ^–] = 10^-2,7 моль/л, [HNO₂] = (с_о - 10^-2,7) моль/л

К_{Д HNO2} = [H⁺] [NO₂^–]/ [HNO₂] Þ

4,6×10^-4 = 10^-2,7×10^-2,7 / (с_о – 10^-2,7)

Þ с_о =0,00214 моль/л.