Выбор параметров устройств дискретизации аналоговых сигналов

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

Московский технический университет связи и информатики

Волго-Вятский филиал

ФАКУЛЬТЕТ СЕТИ И СИСТЕМЫ СВЯЗИ

Курсовая работа

По дисциплине:

«Цифровые системы передачи»

______________________________

Нижний Новгород

Исходные данные:

1) Задание 1.Выбор параметров устройств дискретизации аналоговых сигналов

а) Первый сигнал: f_н = 20 кГц , f_в=700кГц – широкополосный сигнал;

б) Второй сигнал: f_н = 59 кГц , f_в=75кГц – узкополосный сигнал;

2) Задание 2. Исследование защищенности сигнала от помех квантования и ограничения.

U_огр=1.14В -напряжение ограничения;

U_вх=0.6 В – амплитуда гармонического колебания;

А_зкв= А_з =41.5 дБ – защищенность от шумов квантования;

3) Задание 3. Изучение операции кодирования и декодирования

U_огр=1.14В -напряжение ограничения;

U_вх1= -0.7 В- первый сигнал;

U_вх2= 0.3 В – второй сигнал;

Тип кодера: А-87,6/13;

4) Задание 4. Расчёт основных параметров системы цикловой синхронизации

b=7- количество символов в синхрогруппе;

b_k=1,7- количество критических точек;

r₁=3- ёмкость накопителя по выходу из синхронизма;

r₂=1- ёмкость накопителя по входу в синхронизм;

р_в=0,19∙10^-4 – вероятность ошибки в линейном тракте;

5) Задание 5. Временное группообразование ( мультиплексирование)

Построить первые 20 позиций последней строки цикла(последнего субцикла) ЦТС ИКМ-120 с двусторонним согласованием скоростей, если заданы два последовательно переданных поля команд согласования. Считать, что принятые команды истинные. Отметить отсутствие или наличие ошибок в заданных командах.

6)Задание 6. Изучение линейных и стыковых кодов

Задана кодовая последовательность- 11100001011101001110000101110100

Задание №1

Выбор параметров устройств дискретизации аналоговых сигналов

1. Выберите частоту дискретизации широкополосного аналогового цифрового сигнала, рассчитайте период дискретизации.

2. Выберите частоту дискретизации узкополосного аналогового сигнала, рассмотрев два варианта: с переносом спектра аналогового сигнала вниз по частоте и без переноса. Для варианта с переносом укажите значения несущей.

Все частоты дискретизации и несущая частота должны выражаться целыми числами, а промежутки на расфильтровку составлять примерно 10% от верхней частоты среза соответствующего фильтра.

3. Рассчитайте и постройте спектральные диаграммы сигналов АИМ, отвечающие каждой из рассмотренных ситуаций, отметив на них расчётные значения частот.

Исходные данные:

Спектры аналоговых сигналов:

а) Первый сигнал: f_н = 20 кГц , f_в=700кГц – широкополосный сигнал;

б) Второй сигнал: f_н = 59 кГц , f_в=75кГц – узкополосный сигнал;

1.1 Частоту дискретизации широкополосного сигнала выбирают по теореме Котельникова в её классическом варианте: 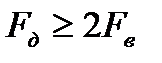(с учётом запаса на расфильтровку).

Fд_min=2∙700=1400 кГц

С учётом полосы расфильтровки (10% от Fв):

Fд=1400+70=1470 кГц

Период дискретизации:

Тд=1/1470∙10³=0.68 мкс

Рис. 1

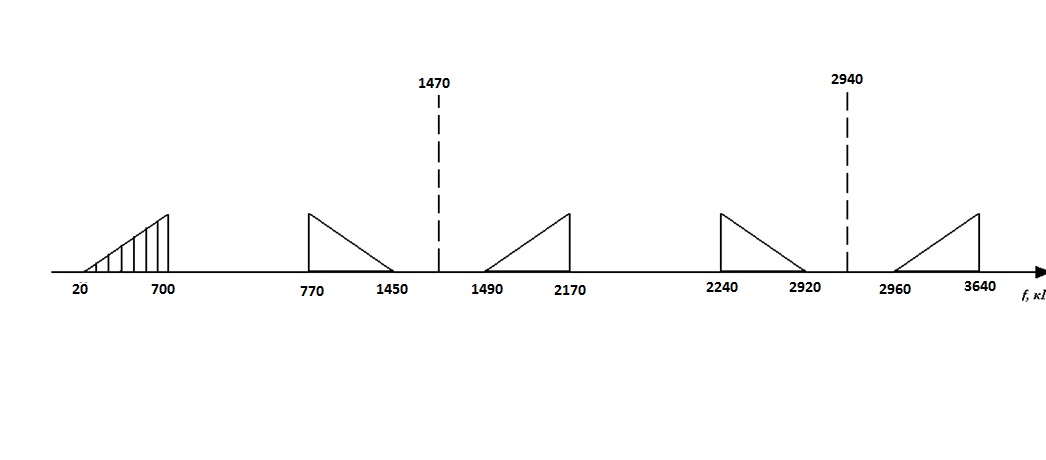
1.2 Частота дискретизации узкополосного аналогового сигнала (55-70кГц)

Отношение верхней частоты к нижней:

Fв/Fн=70/55=1.272<2,

т.е. спектр преобразуемого сигнала меньше октавы, следовательно возможно использовать менее высокую, чем по Котельникову, частоту дискретизации можно определить двумя способами:

Метод переноса исходного спектра в область нижних частот:

Исходя из того, что мы должны приблизить исходный спектр сигнала максимально к нулю

Fд_min=2∙f_В- f_Н =140-55=85 кГц

С учётом полосы расфильтровки (10% от Fв):

Fд=85+7 = 92кГц

Период дискретизации:

Тд=1/92∙10³=10, 86 мкс

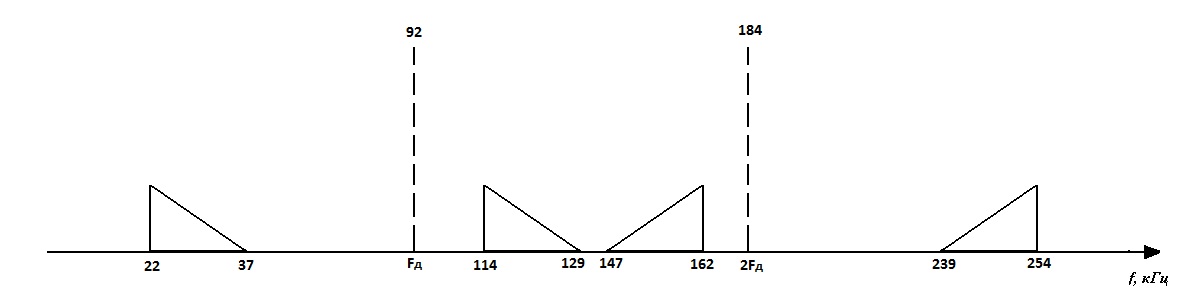
Рис. 2

Методом последовательного приближения

Fв/Fн=70/55=1.272<2,

Исходя из этого условия, можно найти Fд без переноса спектра вниз, применяя условие демодуляции:

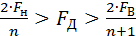, где n=1, 2, 3

Составим таблицу для разных значений «n»:

n=0	∞ > Fд > 150
n=1	118 > Fд > 75
n=2	59 > Fд > 50
n=3	Таблица 1 40 > Fд > 38

Подберём такое «n», чтобы при его значении для F_Д ещё было 10% на полосу расфильтровки (10% от F_В, то есть 7кГц), этой полосе соответствует n=1

Частота дискретизации:

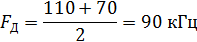
Период дискретизации:

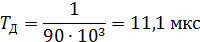
Рис. 3

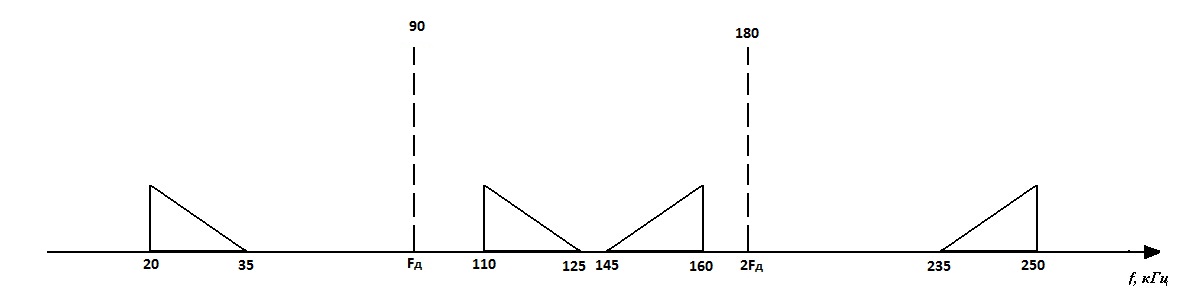
Схемы детектирования:

1) Широкополосного сигнала:

2) Узкополосного с переносом спектра:

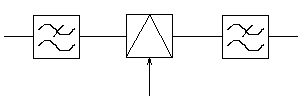
2) Методом последовательного приближения:

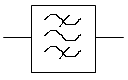
Рис. 4

Вывод: При дискретизации узкополосного сигнала частота дискретизации, найденная по теореме Котельникова, получается слишком высокой. Чтобы её уменьшить целесообразно перенести спектр аналогового сигнала до дискретизации вниз по частоте.

Задание №2

Исследование защищенности сигнала от помех квантования и ограничения

2.1 Определите минимальное количество разрядов m в кодовом слове, при котором обеспечивается заданная защищённость гармонического колебания с амплитудой Um от шумов квантования Азкв при равномерном квантовании. Постройте зависимость защищённости от уровня гармонического колебания при изменении его амплитуды от Um до напряжения ограничения Uогр.

2.2 Приведем для наглядности характеристику помехозащищенности и характеристику компандирования для А-87.6/13

Исходные данные:

U_огр=1.14В -напряжение ограничения;

U_вх=0.6 В – амплитуда гармонического колебания;

А_зкв= А_з =41.5 дБ – защищенность от шумов квантования;

2.1 Защищённость равна:

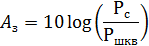
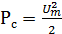– мощность сигнала

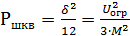-мощность помехи

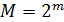- число уровней квантования

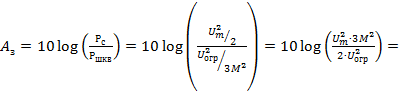
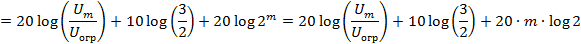
Выразим из этой формулы m:

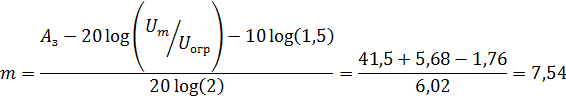
Округлим: m = 8

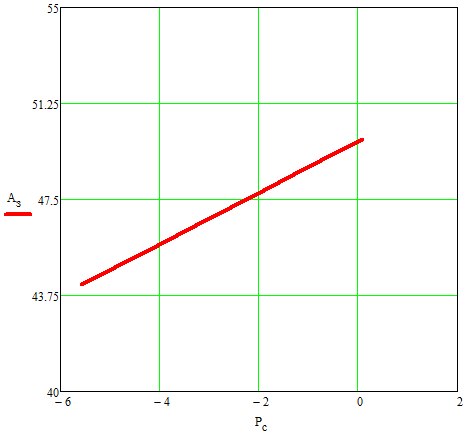
Построим характеристику защищенности от помехи ( 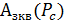) рис.

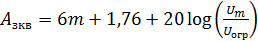
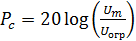
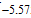
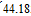
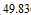
Рис. 5

2.2 Приведем для наглядности характеристику помехозащищенности и характеристику компандирования.

Характеристика защищенности от шумов квантования для характеристики А87.6/13

Рис. 6

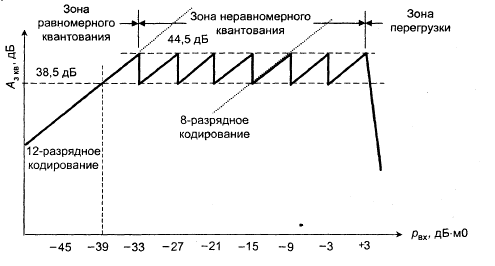
Амплитудная характеристика неравномерного квантующего устройства

Рис. 7

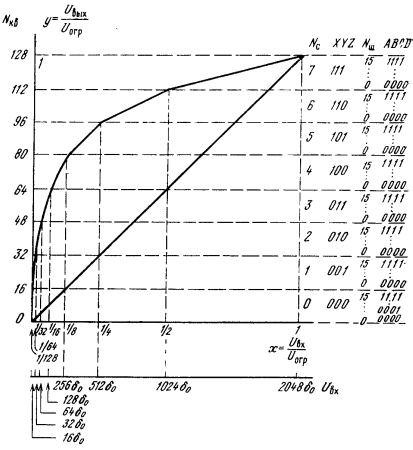
Рис. 7

Вывод: Для обеспечения требуемой защищенности необходимо использовать 8 разрядов. При этом характеристика будет линейно возрастать и лежать выше Азкв.тр., но ниже Uогр.

Задание №3.

Изучение операции кодирования и декодирования

3.1 Для двух отсчётов аналогового сигнала с амплитудами U1 и U2 выполните операции неравномерного квантования и кодирования, осуществляемые в нелинейном кодере с сегментированной характеристикой компрессии А-типа. Определите абсолютные и относительные величины ошибок квантования этих отсчётов и изобразите полученные в результате кодовые слова в виде последовательности токовых и бестоковых посылок в коде БВН.

3.2 Осуществите нелинейное декодирование кодовых слов, полученных в предыдущем пункте, если в указанных заданием разрядах произошли ошибки, то есть вместо символа "1" принят символ "0" и наоборот.

Исходные данные:

U_огр=1.14В -напряжение ограничения; U_вх1= -0.7 В- первый сигнал;

U_вх2= 0.3 В – второй сигнал; Тип кодера: А-87,6/13;

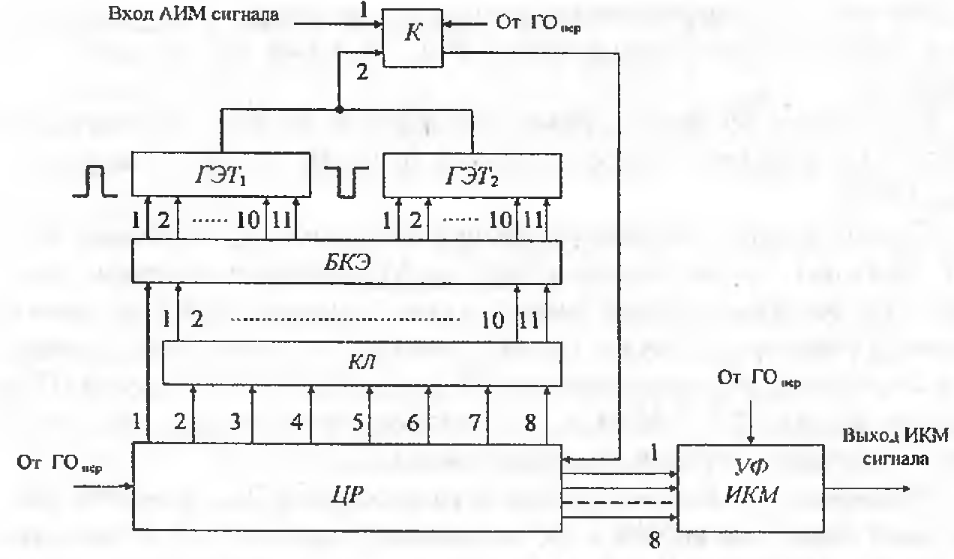Структурная схема кодера с нелинейным квантованием

Рис.8

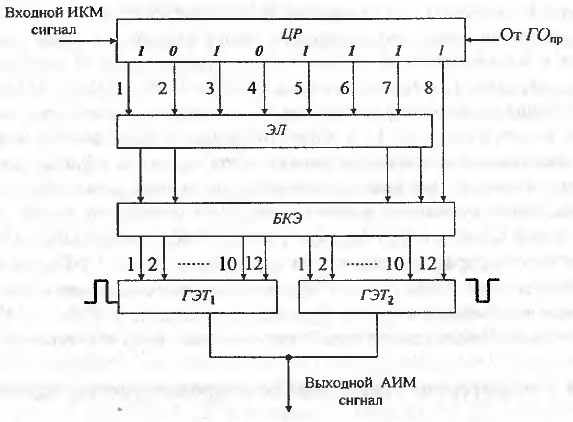
Структурная схема декодера кодека с нелинейным квантованием

Рис.9

Параметры амплитудной характеристики квантующего устройства А87,6/13

Номер сегмента	Код номера сегмента	Размер шага квантования	Нижняя граница сегмента	Верхняя граница сегмента
	000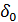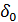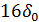
1	001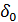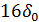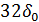
2	010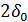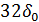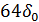
3	011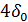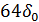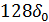
4	100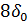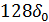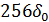
5	101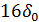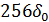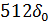
6	110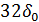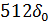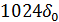
7	111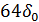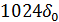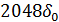

Таблица 2

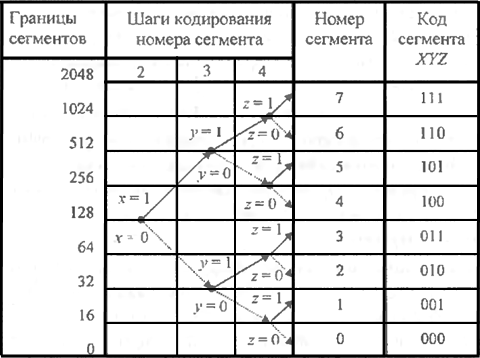
В соответствии с этой характеристикой 8-и разрядное кодовое слово мгновенного значения сигнала имеет структуру PXYZABCD. В этой структуре P – старший разряд указывает полярность сигнала ("1" - положительная, "0" - отрицательная), XYZ – код номера сегмента, а ABCD – код номера шага внутри сегмента.

Минимальный размер шага:

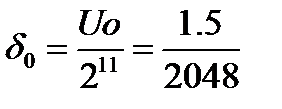=1.14/2048 = 0.0005566=5,566∙10^-4

Согласно заданным значениям, при неравномерном квантовании получим два кодовых слова:

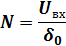
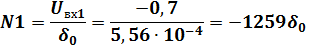
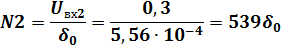
3.1 а) На вход кодера поступает сигнал величиной -1259 ₀. В первом разряде будет сформирован "0": Р=0 (сигнал имеет отрицательную величину). В течение следующих трёх тактов формируются разряды кода номера сегмента (XYZ) по следующему алгоритму:

Таблица 3

По таблице 3 определим код сегмента:

1259>128 X=1

1259>512 Y=1

1259>1024 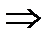Z=1

Код сегмента 111, шаг квантования h=64 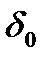с U_нг =1024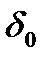

Далее осуществляем кодирование методом взвешивания: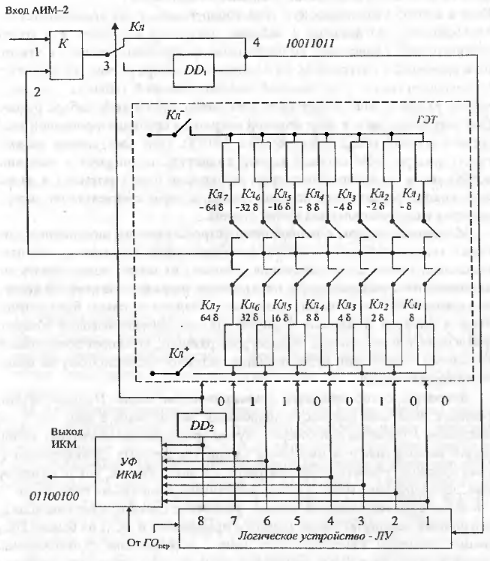

Рис. 10 Линейный кодер взвешивающего типа двухполярного сигнала

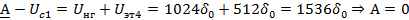
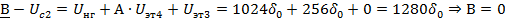
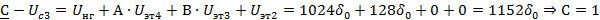
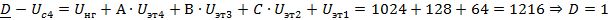
Полученная кодовая комбинация: 01110011

При декодировании будет восстановлено значение:

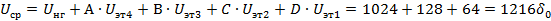
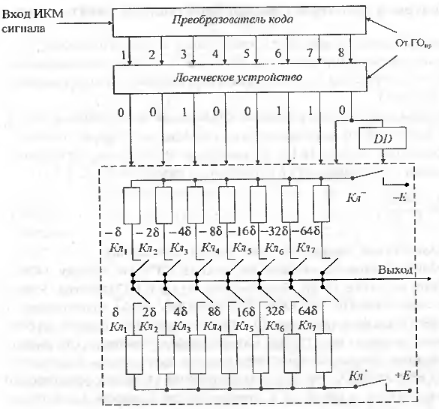
Рис. 11 Линейный декодер взвешивающего типа для двухполярного сигнала.

Рассчитаем величину шума квантования:

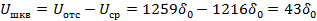
Шум квантования превышает половину шага квантования .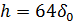

Требуется коррекция!

ABCD⇒0100, сдвинули на разряд выше и проверим

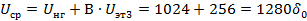
Рассчитаем величину шума квантования:

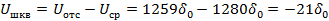
Величина шума квантования, равная -21 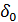входит в границы половины шага квантования. Следовательно исходный код будет выглядеть так:

01110100←PXYZABCD

Расчет абсолютной ошибки декодирования:

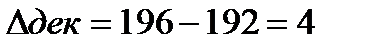1259-1280=21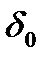

Расчет относительной ошибки:

кв=((1259-1280)/ 1259)*100%=0,016%

б) На вход кодера поступает сигнал величиной 539 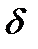_0. В первом разряде будет сформирован "1": Р=1 (сигнал имеет положительную величину). В течение следующих трёх тактов формируются разряды кода номера сегмента (XYZ), определяемые по таблице 3:

539>128 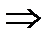X=1

539>512 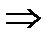Y=1

239>1024 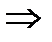Z=0

Код сегмента 110, шаг квантования 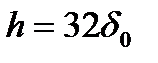с U_нг =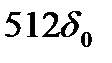

Далее осуществляем кодирование методом взвешивания:

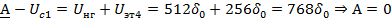
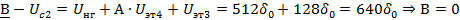
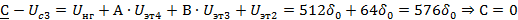
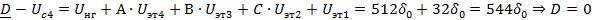
Полученная кодовая комбинация: 11100000

При декодировании будет восстановлено значение:

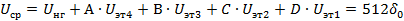
Рассчитаем величину шума квантования:

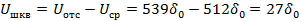
Шум квантования превышает половину шага квантования .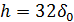

Требуется коррекция!

ABCD⇒0001, сдвинули код сегмента на разряд выше, проверим величину шума квантования при этом коде сегмента.

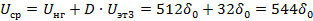
Рассчитаем величину шума квантования:

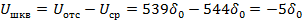
Величина шума квантования, равная -5 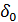входит в границы половины шага квантования. Следовательно исходный код будет выглядеть так:

11100001←PXYZABCD

Расчет абсолютной ошибки декодирования:

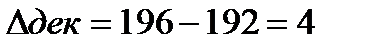539-544=5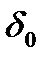

Расчет относительной ошибки:

кв=((539-544)/539)*100%=0,009%

Задание № 4.