Химические реакции, которые при одних и тех же условиях могут идти в противоположных направлениях, называются обратимыми

Например:

H₂ + Cl₂ = 2HCl (t = 200 °C) Реакция необратимая, идет до конца.

Н₂ + I₂ ↔ 2HI (t = 200 °C) Реакция обратимая, до конца не идет.

В уравнении обратимой реакции всегда ставятся двойные стрелки (↔).

Изменение концентраций реагентов (исходных веществ) и продуктов обратимой реакции во времени может быть представлено следующим графиком:

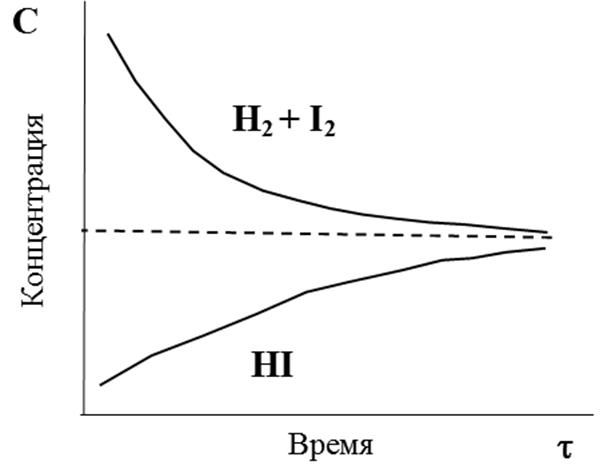
Как видим из графика, концентрации исходных веществ уменьшаются, а концентрации продуктов реакции увеличиваются.

Выражения скоростей прямой и обратной реакций согласно закону действующих масс имеют вид:

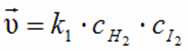
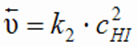
Скорость прямой реакции со временем будет уменьшаться, а скорость обратной реакции - увеличиваться. Наступит такой момент, когда скорости прямой и обратной реакций выровняются:

=

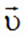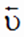
Состояние реакции, в котором скорость обратной реакции становится равной скорости прямой реакции, называется химическим равновесием. Состояние равновесия имеет динамический характер.

Признаки химического равновесия:

1. Наличие всех реагентов в системе;

2. Постоянство их концентраций во времени;

3. Возможность подойти к состоянию равновесия как со стороны прямой реакции, так и со стороны обратной реакции.

Начиная с момента равновесия концентрации всех веществ (реагентов и продуктов реакции) будут оставаться неизменными. Концентрации веществ, соответствующие состоянию равновесия, называются равновесными и обозначаются в виде квадратных скобок: [ ]

Для рассматриваемой выше реакции, находящейся в состоянии равновесия, приравниваем скорости примой и обратной реакций:

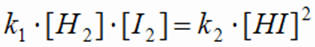
Преобразуя полученное выражение, получим уравнение, представляющее собой математическое выражение закона действующих масс при химическом равновесии.

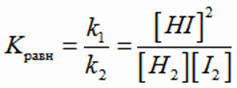
Для условной обратимой реакции аА + bВ 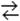сС + dD закон действующих масс записывается следующим образом:

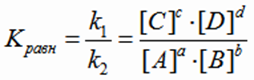
K_равн - константа равновесия, представляет собой отношение констант скоростей прямой и обратной реакций, не зависит от концентраций веществ, но зависит от температуры и природы реагирующих веществ. При данной температуре константа равновесия является постоянной величиной.

Итак, константа равновесия равна отношению произведения равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ, взятых в степенях, равных их стехиометрическим коэффициентам в уравнении реакции.

Примеры:

1. 2SO_2(г) + O_2(г) ↔ 2SO_3(г)

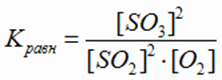
2. СО_2(г) + Н₂О_(ж) ↔ Н₂СО_3(ж) (реакция гетерогенная)

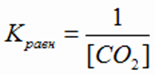
3. Ti_(тв) + 2I_2(г) ↔ TiI_4(г) (реакция гетерогенная)

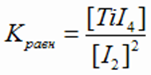
В гетерогенных реакциях в выражения константы равновесия входят концентрации только газовых компонентов.

Для реакций с участием газов константа равновесия может выражаться через парциальные давления (обозначается символом К_р).

Пример. H_2(г) + I_2(г) ↔ 2НI_(г)

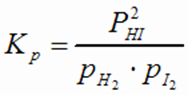
Значение константы равновесия определяет выход реакции.

Выходом реакции называют отношение количества получаемого в действительности продукта к тому количеству, которое получилось бы при протекании реакции до конца (или по расчёту). Выход реакции обычно выражается в процентах. Так, при K_равн>> 1 выход реакции велик, поскольку в этом случае

[C]^c [D]^d >> [A]^a [B]^b

При K_равн << 1 выход реакции мал.

Примеры задач на равновесие.

Пример 1. Исходные концентрации водорода и иода в реакции H_2(г) + I_2(г) ↔ 2HI_(г) равны 1,5 моль/л и 0,9 моль/л соответственно. Вычислите константу равновесия, если известно, что к моменту равновесия прореагировало 40 % Н₂.

Решение. При решении задач на равновесие удобно использовать табличную форму записи. Записываем уравнение реакции и под ним составляем таблицу, состоящую из трех строк.

H_2(г) + I_2(г) ↔ 2HI_(г)

исходные концентрации, моль/л	1,5	0,9
изменение концентраций, моль/л	0,6	0,6	1,2
равновесные концентрации, моль/л	0,9	0,3	1,2

В первой строке таблицы будем записывать исходные концентрации реагентов (или исходных веществ).

Во второй строке - изменение концентраций исходных веществ и продуктов реакции к моменту достижения состояния равновесия.

В третьей строке - равновесные концентрации всех веществ.

Заполнение таблицы происходит постепенно.

По условию задачи даны исходные концентрации водорода и иода, поэтому, заполняя таблицу, в первой строке второй графы под формулами веществ H₂ и I₂ ставим значения их исходных концентраций. А под формулой вещества HI ставим цифру “0”, т.к. в начальный момент времени иодоводорода не было.

По условию задачи к моменту равновесия прореагировало 40 % водорода. Изменение концентрации H₂ составило:

1,5 · 0,4 = 0,6 моль/л

Проставим это значение в таблице во второй строке под водородом.

Руководствуясь уравнением реакции, вычислим изменение концентрации иодоводорода к моменту достижения состояния равновесия:

1 моль Н₂ прореагировал с 1 моль I₂

0,6 моль Н₂ прореагирует с х моль I₂ ,

отсюда х = 0,6 моль I₂

на 1 моль Н₂ получено 2 моля НI

на 0,6 моль Н₂ получено х моль НI ,

отсюда х = 1,2 моль HI

Запишем полученные значения (0,6 и 1,2) в таблице во второй строке под формулами веществ I₂ и HI.

Далее подсчитаем равновесные концентрации водорода, иода и иодаводорода и проставим их значения в таблице в третьей строке.

[H₂] = 1,5 - 0,6 = 0,9 моль/л

[I₂] = 0,9 - 0,6 = 0,3 моль/л

[HI] = 0 + 1,2 = 1,2 моль/л

Поставив значения равновесных концентраций в выражение константы равновесия, получим:

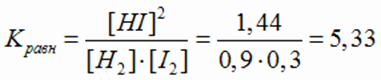
Ответ: константа равновесия равна 5,33.

Пример 2. Равновесие реакции N₂ + 3H₂ ↔ 2NH₃ устанавливается при следующих концентрациях участвующих в них веществ: [N₂] = 0,01 моль/л,

[H₂] = 2,0 моль/л, [NH₃] = 0,4 моль/л. Вычислите константу равновесия и исходные концентрации азота и водорода.

Решение. Записываем уравнение реакции и под ним составляем таблицу.

N₂ + 3H₂ ↔ 2NH₃

исходные концентрации, моль/л	0,21	2,6
изменение концентраций, моль/л	0,2	0,6	0,4
равновесные концентрации, моль/л	0,01	2,0	0,4

По условию задачи даны равновесные концентрации азота, водорода и аммиака.

Вносим значения этих концентраций в третью строку таблицы под соответствующими веществами. Запишем в таблице в первой строке исходную концентрацию аммиака, равную “нулю”.

Исходя из того, что аммиака вначале реакции не было, а равновесная концентрация его равна 0,4 моль/л, то делаем вывод, что аммиака получено в ходе реакции 0,4 моль/л. Записываем это значение в таблице во второй строке под формулой NH₃.

Зная это значение и исходя из уравнения реакции, подсчитаем изменение концентрации азота и водорода. Для этого составим пропорции:

на 1 моль N₂ приходится 2 моля NH₃

на х моль N₂ придется 0,4 моля NH₃ ,

отсюда х = 0,2 моль/л N₂

на 3 моля Н₂ приходится 2 моля NH₃

на х моль Н₂ придется 0,4 моля NH₃ ,

отсюда х = 0,6 моль/л Н₂

Вносим полученные данные в таблицу во вторую строку под формулами N₂и H₂.

Далее подсчитываем исходные концентрации азота и водорода:

Исходная концентрация N₂: 0,01 + 0,2 = 0,21 моль/л

Исходная концентрация H₂: 2,0 + 0,6 = 2,6 моль/л

Подсчитаем константу равновесия.

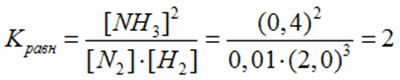
Ответ: K_равн = 2; 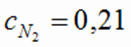моль/л; 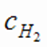= 2,6 моль/л

Пример 3. Рассчитайте равновесные концентрации веществ, участвующих в реакции СО + Н₂О ↔ СО₂ + Н₂, если исходные концентрации веществ равны:

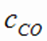= 0,1 моль/л, 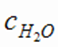= 0,4 моль/л, а константа равновесия при данной температуре равна 1.

Решение. Записываем уравнение реакции и под ним составляем таблицу.

СО + H₂О ↔ СО₂ + Н₂

исходные концентрации, моль/л	0,1	0,4
изменение концентраций, моль/л	а	а	а	а
равновесные концентрации, моль/л	(0,1-а)	(0,4-а)	а	а

По условию задачи даны исходные концентрации веществ СО и Н₂О. Вносим значения этих концентраций в таблицу в первую строку под веществами СО и Н₂О, а под продуктами реакции СО₂ и Н₂ проставляем “нули”.

Далее, поскольку других данных в условии задачи нет (кроме константы равновесия), то задаемся некоторой величиной (обозначим её “а”), считая, что а - это количество вещества СО, израсходованного к моменту равновесия (в моль/л). Проставим величину “а” в таблице во второй строке под веществом СО.

Далее можно найти, сколько прореагировало вещества Н₂О к моменту равновесия, и сколько получено веществ СО₂ и Н₂ к моменту равновесия. Найти эти величины можно, исходя из коэффициентов в уравнении реакции. Коэффициенты в уравнении реакции перед всеми веществами равны “единицы”. Это значит, согласно закону стехиометрии, на 1 моль СО будет израсходован 1 моль Н₂О и будет получено по 1 молю СО₂ и Н₂. А на “а” моль СО будет израсходовано “а” моль Н₂О и получено по “а” моль СО₂ и Н₂. Проставляем значение ‘а” в таблице во второй строке под веществами Н₂О, СО₂ и Н₂.

Равновесные концентрации для исходных веществ будут уменьшены на величину “а”, а для продуктов реакции будут равны величине “а”. Проставляем в таблице выражения равновесных концентраций в третьей строке.

Записываем выражение константы равновесия для данной реакции:

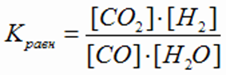
Подставляем выражения равновесных концентраций в данную формулу. По условию задачи К_равн равна 1. Получаем уравнение с одним неизвестным.

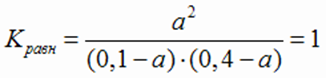
Решая уравнение, находим величину “а”. а = 0,08

Таким образом, равновесные концентрации веществ будут равны:

[CO] = 0,1 - 0,08 = 0,02 моль/л;

[H₂O] = 0,4 - 0,08 = 0,32 моль/л;

[CO₂] = 0,08 моль/л;

[H₂] = 0,08 моль/л.

Ответ: 0,02; 0,32; 0,08; 0,08 (моль/л)