Примеры решения типовых задач. Пример 1. При сгорании 1 кг метана выделилось 50137,5 кДж теплоты
Пример 1. При сгорании 1 кг метана выделилось 50137,5 кДж теплоты. Рассчитайте стандартную энтальпию образования метана ∆НоСН4.
Решение.
1. Пересчитаем количество участвующего в реакции метана, выраженное в граммах, в моли (учитывая, что молярная масса СН4 равна 16 г/моль):
Количество СН4в молях n равно:
n СН4= 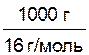 =62,5 моль.
=62,5 моль.
2. Рассчитаем количество теплоты, выделяющееся при сгорании 1 моля метана:
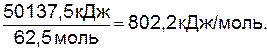
3. Запишем термохимическое уравнение реакции горения метана:
CH4(г) + 2О2(г) = CО2(г) + 2Н2О(г) , Qр=802,2 кДж,
Qр=−∆Нор=(∆НоСО2(г) +2∆НоН2О(г) )−( ∆НоСН4(г) +2∆НоО2(г))=
=[(−393,5)+2(−241,8)−( ∆НоСН4(г))−2(0)]=−802,2 кДж.
Отсюда: ∆НоСН4=(802,2−393,5−483,6)=−74,9 кДж/моль СН4.
Пример 2. Рассчитайте количество теплоты, которое выделится при полном сгорании 100 л этана, взятого в газообразном состоянии при н.у., если в результате реакции образуется СО2(г) и Н2О(г).
Решение.
1. Реакция горения этана выражается термохимическим уравнением
С2Н6(г) + З,5O2(г) = 2CO2(г) + 3Н2О(г); ∆Нр=−1559,87 кДж.
2. Переведем количество участвующего в реакции этана, выраженное в литрах (н.у.), в моли (учитывая, что 1 моль газа при н.у. занимает объем, равный 22,4 л):
Количество этана в молях n равно:
n С2Н6(г)= 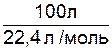 =4,46 моль.
=4,46 моль.
3. Находим значения стандартных энтальпий образования (∆Но298) для всех веществ, участвующих в реакции (Прил. табл. 2) и рассчитываем тепловой эффект в расчете на один моль С2Н6(г):
∆Нореакции=(2∆НоСO2(г) +3∆НоН2O (г))−(∆НоС2Н6(г) +3,5∆НоO2(г))=
= [2(−393,5)+3(−241,8)]−[−84,7+3,5×0]=−1427,7 кДж/моль С2Н6(г).
Qр=−∆Нор=1427,7 кДж.
4. Пересчитаем полученный тепловой эффект на реальное количество этана, т.е. на 4,46 моля (100 л, н.у.):
Qр=−∆Нореальн.=1427,7×4,46=5767,42 кДж.
Пример 3. Не производя вычислений, определите знак изменения энтропии в следующих реакциях. Рассчитайте изменение энтропии для стандартных условий и сравните с результатом оценки.
1) 2NН3(г) = N2(г) + 3H2(г),
2) NH4NO3(тв) = N2O(г) + 2Н2О(г),
3) 2Н2(г) + O2(г) = 2Н2O(г),
4) 2Н2(г) + O2(г) = 2Н2O(ж).
Решение. Изменение энтропии реакции можно оценить качественно в случае реакции с участием газов. При переходе вещества в газообразное состояние происходит сильное увеличение энтропии, превышающее другие факторы, влияющие на энтропию. Поэтому по количеству вещества газов в правой и левой частях уравнения реакции можно определить, возрастает энтропия или уменьшается.
В первой реакции из 2-х молей вещества, находящегося в газообразном состоянии образуется 4 моля веществ, находящихся в газообразном состоянии, следовательно, S1>0.
Изменение энтропии этой реакции в стандартных условиях (∆Sо298) равно:
∆Sо298=SоN2(г)+3SоН2(г)−2SоNН3(г)=191,5+ 3×130,5−2×192,7=197,6 Дж/К.
Во второй реакции 1 моль вещества в твердом состоянии образует 3 моля газообразных веществ, следовательно, ∆S2>0. Изменение энтропии этой реакции в стандартных условиях (∆Sо298) равно:
∆Sо298=SоN2О(г)+2SоН2О(г) –SоNН4NO3(тв) =219,8+2×188,7−151=446,2 Дж/К.
В (3) и (4) реакциях уменьшается как общее число молей, так и число молей газообразных веществ, так что ∆S3<0 и ∆S4<0, при этом DS4 имеет более отрицательное значение, т.е. больше по абсолютной величине чем ∆S3, так как SН2О(г) > SН2О(ж).
Пример 4. Установите возможность восстановления диоксида титана до свободного металла по следующей реакции при стандартных условиях и при 2500 К (зависимостью ∆Hори ∆Sорот температуры пренебречь):
TiO2(тв) + 2С(тв) = Ti(тв) + 2СО(г).
Решение. Из второго закона термодинамики следует, что самопроизвольно протекают только такие реакции, которые сопровождаются уменьшением энергии Гиббса (∆Gр<0).
1. Рассчитаем ∆Gор для стандартных условий с учетом табличных данных (см. прил. табл. 2):
∆Gорекции=(2∆GоСО(г)+∆GоTi(тв))−(∆GоTiO2(тв) +2∆GоС(тв)) =
= [2(−137,1)+0]−[(−888,6)−2×0] =614,4 кДж.
Поскольку ∆Gор>0, реакция при 298 К невозможна.
2. Рассчитаем изменение энергии Гиббса этой реакции для 2500 К, для чего воспользуемся уравнением:
∆Gт=∆Hоp−T∆Sоp.
Находим изменения ∆Hоpи∆Sоpпри стандартных условиях:
∆Hоpеакции=(2∆HоСО(г) +∆Hо Ti(тв))−( ∆Hо TiO2(тв)+2∆Hо С(тв)) =
= [2(−110,5)+0]−[(−943,9)−2×0 ]=722,9 кДж=722900 Дж.
∆Sоpеакции=(2SоСО(г)+ SоTi(тв))−(SоTiO2(тв)+SоС(тв))=
= [2×197,5+30,6]−[50,3-2×5,7 ]=363,9 Дж/К.
∆Gт=∆Hор−T∆Sор=722900−2500×363,9=−186850 Дж.
∆G2500=−186,85 кДж.
Поскольку ∆G2500< 0, то реакция при 2500 К возможна.
Пример 5. Вычислите температуру, при которой в стандартном состоянии установится равновесии реакции:
2 NO2(г) 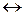 N2O4(г),
N2O4(г),
если известны: ∆Нореакции=−55,3 кДж; ∆Sореакции=−175,8 Дж/К.
Решение. Используя для расчета стандартные значения функций состояния, имеем в виду стандартное состояние системы. Если одновременно это равновесное состояние, то ∆Gореакции=0. Применяем уравнение:
∆Gор=∆Hор−T∆Sор=0.
Преобразуем его и подставляем числовые значения:
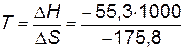 =314,56 К (41,4оС).
=314,56 К (41,4оС).
Система находится в равновесном стандартном состоянии при температуре 41,4 оС.
