Определение внутренних усилий в балках

Внутренними усилиями в каком-нибудь сечении тела или конструкции (балки, арки и др.) называют силы, с которыми части тела, разделенные этим сечением, действуют друг на друга. Метод определения внутренних усилий, аналогичен методу, применяемому при изучении равновесия систем тел. Сначала рассматривают равновесие всего тела (конструкции) в целом и определяют реакции внешних связей. Затем сечением, в котором требуется найти внутренние усилия, разделяют тело на две части и рассматривают равновесие одной из них. При этом, если система действующих на тело внешних сил плоская, то действие отброшенной части заменяется в общем случае плоской системой распределенных по сечению сил; эти силы представляют одной приложенной в центре силой с двумя наперед неизвестными составляющими N (продольная вдоль стержня сжимающая (со знаком+) или растягивающая (со знаком-) и Q (поперечная сила, стремящаяся сдвинуть примыкающую к сечению часть балки) и парой сил с наперед неизвестным моментом М, называемым изгибающим моментом, который растягивает или сжимает соответствующие крайние волокна балки.

Графическое изображение действующих в теле внутренних усилий называется эпюрой.

Правило построения эпюр внутренних усилий:

- эпюра моментов строится со стороны растянутых волокон;

-эпюра поперечных сил стоится согласно ординат сил.

Пример 1.5.1: Определить опорные реакции и внутренние усилия в балке на рисунке 1.5.1. и построить эпюры внутренних усилий возникающих в балке.

Решение:

1.Определяем какие опорные реакции возникают при заданном креплении балки. Так как опоры шарнирные, то реакции опор следующие:

- на опоре А – вертикальная реакция R_A и горизонтальная реакция Н_А;

- на опоре В – вертикальная реакция R_В.

2. Определяем опорные реакции используя третью форму условий равновесия. Для этого составляем следующие формулы:

-Определяем сумму действующих моментов относительно точки В, используя правило, что если вращение по часовой стрелке то знак (+), если против часовой стрелки то знак (-):

∑М_(В)=R_A*2l-P* l =0 R_A=P* l /2 l =6/2=3кН

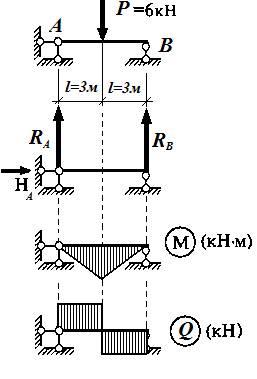
Рисунок 1.5.1

-Определяем сумму действующих моментов относительно точки А:

∑М_(А)= -R_В*2l +P*l =0 R_В= P* l /2 l =6/2=3кН

-Определяем суммы проекций на две координатные оси:

∑_(х)= Н_А=0;

∑_(у)= R_A + R_В –Р= 3+3-6=0.

Проверка показала, что опорные реакции определены правильно.

3.Строим эпюру моментов:

- моменты на опорах отсутствуют, так как опоры шарнирные;

- момент внутренних усилий в точке приложения силы Р (мысленно разрезаем балку в точке приложения силы Р, отбрасываем правую часть и определяем сумму действующих моментов от внешних сил, но так как тело находится в равновесии, то момент внутренних сил равен моменту внешних сил) :

∑М_(Р)= R_A* l = 3*3=9кН*м

Откладываем от оси балки со стороны растянутых волокон ординату действующего момента и соединяем ее с ординатами моментов на опорах.

4.Строим эпюру поперечных сил:

- на левой опоре откладываем ординату равную опорной реакции R_A=3кН

- мысленно разрезаем балку слева в непосредственной близости от точки проложения внешней силы Р и определяем сумму внешних и внутренних сил:

∑_(Рл)= R_A = 3кН

Аналогично определяем внутреннюю силу в непосредственной близости от точки проложения внешней силы Р :

∑_(Рпр)= R_A–Р= 3-6=-3кН

- на правой опоре откладываем ординату равную опорной реакции R_В=3кН.

Пример 1.5.2: Определить опорные реакции и внутренние усилия в балке на рисунке 1.5.2. и построить эпюры внутренних усилий возникающих в балке.

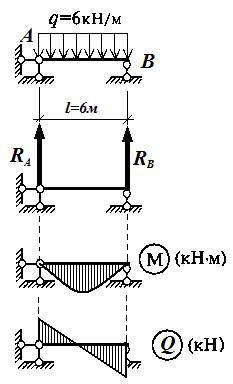
Рисунок 1.5.2.

Решение:

1.Определяем какие опорные реакции возникают при заданном креплении балки. Так как опоры шарнирные, то реакции опор следующие:

- на опоре А – вертикальная реакция R_A и горизонтальная реакция Н_А;

- на опоре В – вертикальная реакция R_В.

2. Определяем опорные реакции используя третью форму условий равновесия. Для этого составляем следующие формулы:

-Определяем сумму действующих моментов относительно точки В, используя правило, что если вращение по часовой стрелке то знак (+), если против часовой стрелки то знак (-):

∑М_(В)=R_A* l -q* l * l /2=0 R_A= q* l * l /2/ l = q* l /2=6*6/2=18кН

-Определяем сумму действующих моментов относительно точки А:

∑М_(А)= -R_В* l + q* l * l /2=0 R_В= q* l * l /2/ l =6*6*3/6=18кН

-Определяем суммы проекций на две координатные оси:

∑_(х)= Н_А=0;

∑_(у)= R_A + R_В – q* l = 18+18-6*6=0.

Проверка показала, что опорные реакции определены правильно.

3.Строим эпюру моментов:

- моменты на опорах отсутствуют, так как опоры шарнирные;

- момент внутренних усилий в точке приложения силы Р (мысленно разрезаем балку в точке приложения силы Р, отбрасываем правую часть и определяем сумму действующих моментов от внешних сил, но так как тело находится в равновесии, то момент внутренних сил равен моменту внешних сил) :

∑М_(Р)= R_A* l /2- q* l/2 * l/4 = q* l /2* l /2- q* l² /8= q* l² /8=6*6²/8= 4,5кН*м

Откладываем от оси балки со стороны растянутых волокон ординату действующего момента и соединяем ее плавно с ординатами моментов на опорах.

4.Строим эпюру поперечных сил:

- на левой опоре откладываем ординату равную опорной реакции R_A=18кН

- мысленно разрезаем балку по середине и определяем сумму внешних и внутренних сил:

∑_(центр)= R_A - q* l /2=18-6*6/2= 0кН

- на правой опоре откладываем ординату равную опорной реакции R_В=3кН.

Аналогичным образом строятся эпюры моментов и поперечных сил балок представленных на рисунках 1.5.3 и 1.5.4.

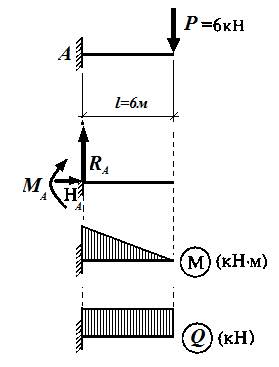
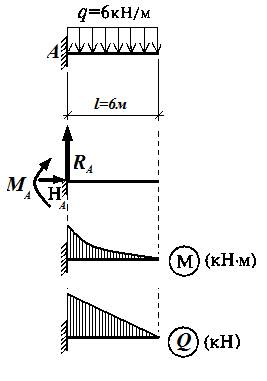
Рисунок 1.5.3 Рисунок 1.5.4.

1.5.2 Трехшарнирная арка со сплошной стенкой.

Для расчета трехшарнирной арки применим следующий метод.

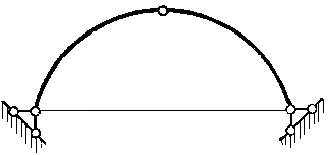
Рисунок 1.5.5

Исключим средний шарнир арки, заменив его жесткой связью между половинами арки, и удалим одну горизонтальную опору. Полученная новая система представляет собой статически определимую однопролетную балку с криволинейной осью (рис. 1.5.5, а). Отброшенную горизонтальную опору заменяем усилием Н — неизвестным пока распором арки.

От действия внешней нагрузки строим вдоль горизонтальной проекции арки эпюру моментов, как в обычной балке (рис. 1.5.6, б). От действия единичного усилия Н= 1 также строим эпюру моментов, ординаты которой будут совпадать с ординатами оси арки (рис. 1.5.6, в). Окончательную эпюру моментов в арке можно вычислить по формуле

М= М^б – Нf (1.5.1)

где М^б- ординаты балочной эпюры моментов от действия внешних сил,

f - ординаты оси арки и эпюры моментов в криволинейной балке от единичного распора Н

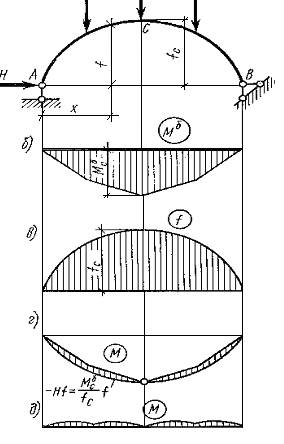
Рисунок 1.5.6

В точке С расположения среднего шарнира момент в арке должен быть равен нулю: ,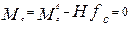

отсюда получаем: 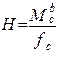(1.5.2)

подставляя в формулу (1.5.1) значение распора получаем:

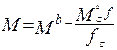(1.5.3)

В описанном методе использован принцип основной системы, которая получается из заданной путем введения и отбрасывания некоторых связей. Этот принцип широко применяется в классических методах расчета статически неопределимых систем, а иногда и для расчета статически определимых систем, как в данном случае.

Другой способ определения распора и усилий в трехшарнирных арках заключается в расчете каждой половины арки на действующую на нее нагрузку как балки, шарнирно опертой одним концом и опирающейся другим концом на подвижную опору, которой здесь служит другая половина арки. Реакция этой подвижной опоры направлена через концевые шарниры второй половины арки. Реакция другой опоры будет направлена в точку пересечения реакции первой опоры с равнодействующей внешних сил, действующих на половину арки. поскольку иначе не будет равновесия этой поло вины. Определение этих реакций и изгибающих моментов в половине арки производится по простым законам статики. Таким же образом производится расчет и второй половины арки.

Продольные и поперечные силы в любом сечении арки определятся из условия равновесия части арки, расположенной по одну сторону от рассматриваемого сечения. Предварительно заметим, что сумма вертикальных сил, приложенных слева от заданного сечения, равна балочной поперечной силе в спрямленной балке, свободно лежащей на крайних опорах арки и нагруженной заданной вертикальной нагрузкой.

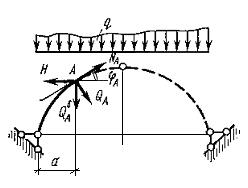
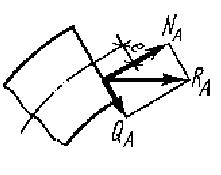
Рисунок 1.5.7 Рисунок 1.5.8

Проектируя все силы, действующие слева от сечения х =а, на направление касательной к оси арки в точке А (рис. 1.5.7), получим продольную силу:

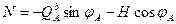(1.5.4)

где 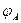— угол наклона касательной к оси арки в точке А.

Проектируя те же силы на направление нормали к оси арки, получим поперечную силу:

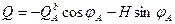(1.5.5)

Если на арку действует не только вертикальная, но и горизонтальная нагрузка р, то вместо распора Н в формулах (2.1.4) и (2.1.5) следует взять сумму всех горизонтальных сил, действующих на арку слева от точки А.

Разделив момент М_А на продольную силу N_A получим эксцентриситет ее действия в сечении арки, который определит точку пересечения равнодействующей внутренних сил в сечении арки с плоскостью этого сечения (рис. 1.5.8). Геометрическое место таких точек, построенных для всех сечений арки, называется кривой давления арки (рис. 1.5.9).

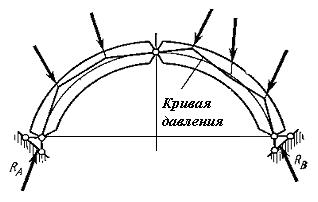
Рисунок 1.5.9

Эта кривая представляет собой линию действия внутренней силы, передающейся вдоль арки. Она равна тангенсу угла между касательными к кривой давления распора к оси арки в том же сечении.

В особых случаях кривая давления может совпадать с осью арки. При этом изгибающие моменты по всей арке будут равны нулю. Такой случай будет, например, при нагрузке круговой арки равномерной радиальной нагрузкой (рис. 1.5.10) или при нагружении параболической арки равномерной Вертикальной нагрузкой (рис. 1.5.11).

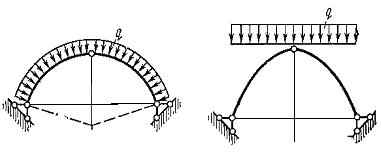
Рисунок 1.5.10 Рисунок 1.5.11

Очертание оси арки, совпадающее с кривой давления, является оптимальным, т. е. наиболее выгодным при данной нагрузке.