Изменение энтропии в химических реакциях

Изменение энтальпии в химических реакциях.

В большинстве курсов химической термодинамики рассматривается три закона. Однако для строгого определения термического равновесия в 1931 г. англ. Р.Фаулер сформулировал закон, который называют нулевым: Две системы, находящиеся в термическом равновесии с третьей системой, состоят в термическом равновесии друг с другом.

Первый закон термодинамики – одна из форм закона сохранения энергии.
Его формулировки: Энергия не создается и не уничтожается.
Вечный двигатель (perpetuum mobile) первого рода невозможен.
В любой изолированной системе общее количество энергии постоянно.

Энергетический эффект химической реакции может проявляться как чисто тепловой, связанный с изменением внутренней энергии системы, например реакция нейтрализации в разбавленном растворе: H⁺+OH^-=H₂O+57кДж

Для этого случая можно записать, что весь тепловой эффект Q при постоянном объеме равен изменению внутренней энергии

U: Q_v = U

Однако если смешать в пробирке водные растворы карбоната натрия и соляной кислоты и быстро закрыть пробирку пробкой, то через некоторое время система совершит механическую работу, "выстрелив" пробкой. При этом температура растворов после реакции практически не изменяется. Работа совершается, когда повышенное давление в закрытой пробирке уравнивается с атмосферным после вылетания пробки. Таким образом, можно описать работу, как работу расширения газа, совершенную при постоянном давлении (изобарный процесс): p V

В общем случае, работа, совершаемая химической реакцией при постоянном давлении, состоит из изменения внутренней энергии и работы расширения: Q_p = U + p V

Для большинства химических реакций, проводимых в открытых сосудах, удобно использовать функцию состояния, приращение которой равно теплоте, полученной системой в изобарном процессе. Эта функция называется энтальпия (от греч. "энтальпо" – нагреваю):

Q_p = H = U + p V

Другое определение: разность энтальпий в двух состояниях системы равна тепловому эффекту изобарного процесса.

Существуют обширные таблицы, содержащие данные по стандартным энтальпиям образования веществ H^o₂₉₈ . Индексы означают, что для химических соединений приведены энтальпии образования 1 моль их из простых веществ, взятых в наиболее устойчивой модификации (кроме белого фосфора – не самой устойчивой, а самой воспроизводимой формы фосфора) при 1 атм (1,01325^.10⁵ Па или 760 мм.рт.ст) и 298,15 К (25^оС). Если речь идет об ионах в растворе, то стандартной является концентрация 1 М (1 моль/л). В принципе, можно попытаться вычислить абсолютные значения энтальпий для химии (тепловой эффект образования 1 моль соединения из бесконечно удаленных атомов, взятых при 0^оК) или для физики (исходя из элементарных частиц, взятых при 0^оК), но для реальных расчетов общепринятый произвольный уровень отсчета вполне удобен. Знак энтальпии определяется "с точки зрения" самой системы: при выделении теплоты изменение энтальпии отрицательно, при поглощении теплоты изменение энтальпии положительно.

Вернемся теперь к реакции раствора соды с раствором соляной кислоты:

Na₂CO₃ + 2 HCl = 2 NaCl + H₂O + CO₂ ­
Для такой записи мы скорее всего не найдем нужных табличных данных – есть значения H^o₂₉₈ для твердых солей и газообразного хлороводорода, а наша реакция происходила при сливании двух растворов. Чтобы произвести правильный расчет, нужно определить, что на самом деле реагирует:

CO₃^2- + 2 H⁺ = H₂O(ж) + CO₂ ^­

H^o₂₉₈ ,кДж/моль -677 0 -286 -394

По закону Гесса получаем для реакции H^o₂₉₈ = -3 кДж.

Изменение энтропии в химических реакциях.

Вполне очевидно, что реакции с суммарным уменьшением энтальпии (экзотермические) могут идти самопроизвольно, как катящийся с горы камень. Однако хорошо известно, что самопроизвольно идут также некоторые реакции, сопровождающиеся увеличением энтальпии и охлаждением реактора (эндотермические).

Для характеристики эндотермических процессов и определения условий их самопроизвольного осуществления была введена новая функция состояния – энтропия (от греч. "эн" – "в", "внутрь" и "тропе" – "поворот", "превращение"). Изменение энтропии равно (по определению) минимальной теплоте, подводимой к системе в обратимом (все промежуточные состояния равновесны) изотермическом процессе, деленной на абсолютную температуру процесса:

S = Q_мин./T

На данном этапе изучения термодинамики следует принять как постулат, что существует некоторое экстенсивное свойство системы S, называемое энтропией, изменение которого так связано с процессами в системе:

В самопроизвольном процессе S > Q_мин./T

В равновесном процессе S = Q_мин./T

В несамопроизвольном процессе S < Q_мин./T

Для изолированной системы, где dQ = 0, получим:

В самопроизвольном процессе S > 0

В равновесном процессе S = 0

В несамопроизвольном процессе S < 0

В общем случае энтропия изолированной системы или увеличивается, или остается постоянной:

Понятие энтропии возникло из полученных ранее формулировок второго закона (начала) термодинамики. Энтропия – свойство системы в целом, а не отдельной частицы. Второе начало по У.Томсону (1851): "в природе невозможен процесс, единственным результатом которого была бы механическая работа, совершенная за счет охлаждения теплового резервуара". По Р.Клаузиусу (1850): "теплота сама по себе не может перейти от более холодного тела к более теплому" или: "невозможно сконструировать машину, которая, действуя посредством кругового процесса, будет только переносить теплоту с более холодного тела на более теплое".

Самая ранняя формулировка второго начала термодинамики появилась раньше первого начала, на основании работы фр. С.Карно (1824) и ее математической интерпретации фр. Э.Клапейроном (1834) как КПД идеальной тепловой машины:

КПД = (T₁ - T₂)/T₁

Карно и Клапейрон сформулировали закон сохранения теплорода – невесомой неуничтожимой жидкости, содержание которой определяет температуру тела. Теория теплорода господствовала в термодинамике до середины XIX века, при этом законы и соотношения, выведенные на основе представлений о теплороде, оказались действительными и в рамках молекулярно-кинетической теории теплоты. В 1911 г. Макс Планк предложил следующий постулат: энтропия правильно сформированного кристалла чистого вещества при абсолютном нуле равна нулю. Этот постулат может быть объяснен статистической термодинамикой, согласно которой энтропия есть мера беспорядочности системы на микроуровне: S = k_blnW "уравнение Больцмана", выведено М.Планком в 1900 г. W – число различных состояний системы, доступное ей при данных условиях, или термодинамическая вероятность макросостояния системы. k_b = R/N_A = 1,38^.10^-16 эрг/град – постоянная Больцмана. В 1872 г. Л.Больцман предложил статистическую формулировку второго закона термодинамики: изолированная система эволюционирует преимущественно в направлении большей термодинамическоой вероятности.

Следует всегда помнить, что второй закон термодинамики не является абсолютным; он теряет смысл для систем, содержащих малое число частиц, и для систем космического масштаба. Второй закон, особенно в статистической формулировке, неприменим к живым объектам, которые представляют собой открытые системы и постоянно уменьшают энтропию, создавая идеально упорядоченные молекулы, например, за счет энергии солнечного света. Введение энтропии дало возможность установить критерии, позволяющие определить направление и глубину протекания любого химического процесса (для большого числа частиц в равновесии). Макроскопические системы достигают равновесия, когда изменение энергии компенсируется энтропийной составляющей:

При постоянном объеме и температуре:

U_v = T S_v или (U-TS) F = 0 энергия Гельмгольца или изохорно-изо- термический потенциал

При постоянном давлении и температуре:

H_p = T S_p или (H-TS) G = 0 энергия Гиббса или свободная энергия Гиббса или изобарно-изотермический потенциал

Изменение энергии Гиббса как критерий возможности химической реакции

Для данной температуры G = H - T S
При G < 0 реакция возможна;
при G > 0 реакция невозможна;
при G = 0 система находится в равновесии.

Возможность самопроизвольной реакции в изолированной системе определяется сочетанием знаков энергетического (энтальпийного) и энтропийного факторов:

Знак H + - - +

Знак S - + - +

Возможность

самопроизвольной реакции Нет Да Зависит от соотношения

H и T S

Имеются обширные табличные данные по стандартным значениям G⁰ и S⁰ (для энтропии по третьему закону есть нулевой уровень отсчета и соответственно абсолютные значения), позволяющие вычислить G⁰ реакции.

В случае, если температура отличается от 298 К и концентрации реагентов – от 1 М, для процесса в общем виде:

aA + bB cC + dD

G = G⁰ + RT ln([C]^c[D]^d/[A]^a[B]^b)

В положении равновесия G = 0 и G⁰ = -RTlnK_р, где

K_р = [C]^c_равн[D]^d_равн/[A]^a_равн[B]^b_равн константа равновесия

K_р = exp(-G⁰/RT)

Пользуясь приведенными формулами, можно определить температуру, начиная с которой эндотермическая реакция, при которой возрастает энтропия, становится легко осуществимой. Температура определяется из условия:

G⁰ = H⁰ - T S⁰ = 0; T = H⁰/ S⁰

Следует учесть, что для точных расчетов при температурах, заметно отличающихся от 298 К, необходимо использовать для всех термодинамических функций их зависимости от температуры. Например, для реакции: 2 CH₄ = C₂H₄ + 2 H₂

В первом приближении H⁰ = 48,3 ккал/моль C₂H₄;
во втором приближении H_T = 46370 + 6,47T кал/моль

Почти все химические реакции протекают с выделением или поглощением энергии в виде тепла, света, электричества, механической энергии (взрыв) и др. Поглощение или выделение энергии связано с тем, что при протекании реакций одни связи разрываются (в исходных молекулах), на что необходимо затратить энергию. Другие связи образуются (в образующихся молекулах), при этом энергия выделяется. Реакции, протекающие с выделением энергии, называются экзотермическими (например, СН₄ + 2О₂ ® СО₂ + 2Н₂О + Q). Реакции, при протекании которых энергия поглощается, называются эндотермическими (например, N₂ + O₂ ® 2NO – Q).

Система – это тело или группа тел, связанных между собой и мысленно или физически выделенных из окружающей среды.

Внутренняя энергия системы (Е) – это общий запас энергии системы, включая сюда все виды энергии молекул, атомов, электронов и энергию внутри ядра (кроме потенциальной и кинетической энергии системы в целом).

Внутренняя энергия тела (или системы) зависит от природы тела (водород, вода), массы тела и условий существования данного тела (температура, давление). Абсолютное значение «Е» тела измерить пока нельзя. Обычно измеряют изменение внутренней энергии DЕ, происходящее в процессе перехода системы из первого состояния во второе, например:

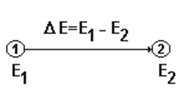
Энтальпия (Н) связана с внутренней энергией (Е) соотношением:

Н = Е + рV,

где р – давление,

V – объем системы.

Абсолютное значение Н (как и Е) измерить нельзя, а измеряют только изменение DН = Н₂ – Н₁ для какого либо процесса (аналогично DЕ).

Н и Е – это функции, характеризующие состояние системы, поэтому DН и DЕ не зависят от пути процесса, а зависят только от начального (Н₁ и Е₁) и конечного (Н₂ и Е₂) состояний системы.

Единицы измерения DН и DЕ – это Дж, кДж, кал и ккал.

Для эндотермических процессов DН>0, а для экзотермических процессов DН<0.

Тепловые эффекты химических реакций.

Почти все химические реакции сопровождаются тепловым эффектом. Тепловой эффект – это количество выделяемого или поглощаемого тепла в реакции, протекающей при определенных условиях. Тепловой эффект приводится обычно для одного моля основного вещества и измеряется в Дж, кДж, килокалориях (ккал), причем 1 ккал = 4,184кДж.

Раздел химии, изучающий тепловые эффекты реакций, называется термохимией.

Обычно все процессы проводятся или в закрытом сосуде, т.е. при постоянном объеме (изохорные процессы, когда V = const) или в открытом сосуде, т.е. при постоянном давлении (изобарные процессы, когда р = const). При этом тепловой эффект изохорно-изотермиче-ского процесса (когда V и Т постоянны) равен изменению внутренней энергии, т.е. Q_v = - DE, а изобарно-изотермического процесса (когда р и Т постоянны) тепловой эффект равен изменению энтальпии, т.е. Q_p = - DH.

Тепловые эффекты реакций можно включать в уравнения реакций.

Химические уравнения, записанные с указанием теплового эффекта, называются термохимическими.

Величина теплового эффекта указывается обычно в правой части уравнения со знаком плюс для экзотермической реакции и со знаком минус для эндотермической реакции, причем термохимические уравнения могут иметь дробные коэффициенты (1/2, 3/2 и др.), например:

Н_2(газ) + ½ О_2(газ) = Н₂О_(газ) + 241,8кДж;

N₂ + O₂ = 2NO – 180,8кДж.

Тепловые эффекты в приведенных примерах записаны термохимическим способом и обозначаются Q, т.е. для первой реакции Q = + 241,8кДж, а для второй реакции Q = - 180,8кДж.

Тепловые эффекты реакций можно выражать через DН, причем DН = - Q. В этом случае термохимические уравнения записывают так:

Н_2(газ) + 1/2О_2(газ) = Н₂О_(газ); DН = - 241,8кДж;

N₂ + O₂ = 2NO; DН = + 180,8кДж.

Закон Гесса.

Для расчетов тепловых эффектов различных процессов используется закон, установленный русским ученым Гессом в 1840 году:

Тепловой эффект реакции не зависит от пути ее протекания, а зависит только от начального и конечного состояния веществ, участвующих в реакции.

Это основной закон термохимии. Закон Гесса выполняется только для процессов, протекающих при следующих условиях:

а) Т = const, V = const (т.е. изохорно-изотермический процесс);

б) Т = const, р = const (т.е. изобарно-изотермический процесс).

Пример использования закона Гесса: из исходных веществ А и В можно получить конечные продукты Д и Е двумя путями: 1 путь – сразу по одной реакции из А и В получаются продукты Д и Е, причем тепловой эффект этой реакции равен DН₁; 2 путь – вещества Д и Е получаются из А и В в несколько реакций, тепловые эффекты которых равны DН₂, DН₃ и DН₄. Закон Гесса утверждает, что тепловые эффекты будут связаны таким соотношением:

DН₁ = DН₂ + DН₃ + DН₄

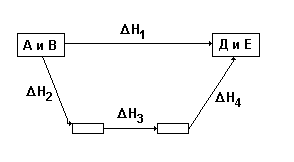
При расчетах тепловых эффектов химических реакций на основе закона Гесса используются энтальпии образования и энтальпии сгорания веществ.

Энтальпия образования вещества - это изменение энтальпии реакции образования одного моля вещества из простых веществ, например:

Н_2(г) + 1/2О_2(г) = Н₂О_(г); DН°_{298 обр.} = -241,8кДж/моль,

т.е. энтальпия образования газообразной воды при стандартных условиях равна -241,8кДж на 1 моль воды. Для различных веществ энтальпии образования приводятся в справочниках при стандартных условиях (т.е. при температуре 298К и давлении 1 атм. или 1,013×10⁵ Па) и обозначается как DН°_{298 обр.}. Отметим, что энтальпии образования простых веществ (О₂, Н₂, Cl₂ и др.) равны нулю.

Энтальпия сгорания вещества – это изменение энтальпии реакции окисления одного моля вещества кислородом до образования его конечных продуктов окисления. Стандартные энтальпии сгорания (т.е. при 298К и 1 атм.) обозначаются DН°_{298 сгор.} и приводится для различных веществ в справочниках.

Если известны энтальпии образования веществ, участвующих в реакции, то на основании закона Гесса можно рассчитывать тепловой эффект этой реакции следующим образом:

Изменение энтальпии реакции (т.е. тепловой эффект реакции) равно сумме энтальпий образования продуктов реакции минус сумма энтальпий образований исходных веществ (при этом учитываются коэффициенты в уравнении реакции).

Например, для реакции аА + bВ ® dD + еЕ получаем:

DН°_{298 реакции} = (d×DН°_{298 обр. (D)} + e×DН°_{298 обр. (E)}) – (a×DН°_{298 обр. (A)} + b×DН°_{298 обр. (B)}).

Подставляя численные значения энтальпий образования продуктов реакции D и Е и исходных веществ А и В, найденные в справочнике, определяем тепловой эффект этой реакции DН°_{298 реакции} (при стандартных условиях).

Тепловой эффект реакции можно определить и по энтальпиям сгорания веществ, а именно:

Изменение энтальпии реакции равно сумме энтальпий сгорания исходных веществ минус сумма энтальпий сгорания продуктов реакции (при этом учитываются коэффициенты в уравнении реакции).

Например, для реакции аА + bВ ® dD + еЕ получаем:

DН°_{298 р-ции} = (аDН°_{298 сгор. (А)} + bDН°_{298 сгор. (В)}) – (d×DН°_{298 сгор. (D)} + е×DН°_{298 сгор. (Е)}).

Это есть тепловой эффект реакции нейтрализации 1 моля эквивалента кислоты 1 молем эквивалента основания.

Если взять сильную кислоту HCl и сильное основание NaOH, то уравнение реакции нейтрализации имеет вид:

HCl + NaOH = NaCl + H₂O + Q_нейтр.

В ионной форме:

H⁺ + Cl^- + Na⁺ + OH^- ® Na⁺ + Cl^- + H₂O или

H⁺ + OH^- ® H₂O + 57,22кДж/моль×экв.

Таким образом, реакция нейтрализации сильной кислоты и сильного основания сводится к образованию H₂O из ионов H⁺ и OH^- и тепловой эффект этой реакции постоянный и равен 57,22кДж/моль×экв., а изменение энтальпии DН°₂₉₈ = - 57,22кДж/моль×экв.

Таким образом, энтальпия нейтрализации сильных кислот и сильных оснований (рассчитанная на 1 моль эквивалента кислоты и основания) постоянная и равна DН°₂₉₈ = - 57,22кДж/моль×экв. (или – 13,75ккал/моль×экв.).

При нейтрализации слабых кислот (Н₂СО₃, Н₂S, HCN и др.) и слабых оснований (NH₃ и др.) энтальпия нейтрализации меньше (по абсолютной величине), так как при этом затрачивается энергия на ионизацию кислоты или основания.

Энтропия есть мера неупорядоченности (беспорядка) системы. Чем больше беспорядок системы, тем больше численное значение энтропии, а значит, это состояние системы будет наиболее вероятным. Поэтому, все процессы, связанные с увеличением беспорядка в системе, сопровождаются возрастанием энтропии: расширение газа, растворение твердых веществ в жидкости, плавление твердого вещества, кипение жидкости. И, наоборот, все процессы, связанные с увеличением в системе упорядоченности (т.е. уменьшением беспорядоченности) сопровождаются уменьшением энтропии: охлаждение газа, сжатие газа, кристаллизация и др.

Энтропия рассчитывается по уравнению Больцмана:

S = K×lnW, где

S – энтропия системы;

К – постоянная Больцмана (К = R/N₀, где R – газовая постоянная, а N₀ – число Авагадро);

W – вероятность состояния системы (W обычно имеет очень большие значения).

Энтропия имеет размерность энергии, деленной на температуру, и обычно она относится к 1 молю вещества, поэтому выражается в Дж/моль×К. В справочниках приведены стандартные энтропии веществ, то есть при 298К и давлении 1 атм. или 1,013×10⁵ Па (обозначается S°₂₉₈). Энтропия простых веществ (Н₂, О₂ и др.) не равна нулю и тоже приводится в справочниках.

Отметим, что энтропия вещества в газообразном состоянии значительно больше, чем в жидком состоянии, а в жидком состоянии больше, чем в твердом состоянии (во всех случаях берем 1моль данного вещества). Например,

S_{H 2O(газ)}>>S_H2O(ж)>S _H2O(тв)

Изменение энтропии реакции (DS°₂₉₈ реакции) равно сумме энтропий продуктов реакции минус сумма энтропий исходных веществ (с учетом коэффициентов в уравнении реакции).

Например, для реакции аА + bВ ® dD + еЕ получаем:

DS°_{298 реакции} = (d×DS°_{298 (D)} + e×DS°_{298 (E)}) - (a×DS°_{298 (A)} + b×DS°_{298 (B)}).

Стандартные энтропии веществ S°_{298 (D)}, S°_{298 (E)} и так далее находят в справочниках.

Для определения возможности и направления протекания химической реакции существуют два фактора: энтальпийный фактор (DН) и энтропийный фактор (DS). Если изменение энтальпии химической реакции DН<0, то энтальпийный фактор способствует самопроизвольному протеканию реакции в прямом направлении, то есть слева направо (®), а если DН>0, то энтальпийный фактор способствует протеканию реакции в обратном направлении ().

Если изменение энтропии химической реакции ∆S > 0, то энтропийный фактор способствует самопроизвольному протеканию реакции в прямом направлении (→), а если ∆S < 0, то энтропийный фактор способствует протеканию реакции в обратном направлении (←).

Влияние обоих факторов (то есть DН и DS) на направление протекания химических реакций учитывает изменение энергии Гиббса DG, которое равно:

DG = DН - ТDS, где

DG – изменение энергии Гиббса химической реакции;

DН и DS – это изменение энтальпии и энтропии химической реакции;

Т – температура в °К.

Изменение энергии Гиббса DG служит критерием самопроизвольного протекания изобарно-изотермических реакций (то есть реакций при постоянной температуре и постоянном давлении), а именно:

При постоянстве температуры и давления химические реакции могут самопроизвольно протекать только в таком направлении, при котором энергия Гиббса уменьшается, то есть изменение энергии Гиббса реакции DG<0.

1) Если DG < 0, то реакция возможна в прямом направлении (®).

2) Если DG > 0, то реакция возможна в обратном направлении ().

3) Если DG = 0, то наступило состояние термодинамического равновесия.

Таким образом, чтобы определить направление реакции, надо рассчитать изменение энергии Гиббса этой реакции (DG _{реакции}). Для расчета DG _{реакции} используются энергии Гиббса образования веществ при стандартных условиях DG°₂₉₈, которые приводятся в справочниках.

Энергия Гиббса образования вещества –это изменение энергии Гиббса в реакции образования одного моля вещества из простых веществ. Обозначается DG°₂₉₈ и относится к 1 молю вещества при стандартных условиях; обычно выражается в кДж/моль. При этом для простых веществ DG°₂₉₈ равно нулю.

Изменение энергии Гиббса химической реакции (DG°_{298 реакции}) равно сумме энергий Гиббса образования продуктов реакции минус сумма энергий Гиббса образования исходных веществ (с учетом коэффициентов в уравнении реакции). Например, для реакции:

аА + bВ ® dD + еЕ

DG°_{298 реакции} = (d×DG°_{298 (D)} + e×DG°_{298 (E)}) - (a×DG°_{298 (A)} + b×DG°_{298 (B)}).

Изменение энергии Гиббса реакции можно рассчитать также, определив изменение энтальпии реакции (DН _{реакции}) и изменение энтропии реакции (DS _{реакции}), то есть DG реакции = DН _{реакции} - Т×DS _{реакции}.

Пример. Рассчитать при 298К изменение энтальпии, энтропии и изменение энергии Гиббса реакции 2NO₂ « N₂O₄, если даны энтальпии образования и энтропии веществ, участвующих в данной реакции
(таблица 8).

Таблица 8 – Стандартные энтальпии образования DН°_298, энтропии S°₂₉₈ некоторых веществ при 298 К (25°С)

Вещество	DН°298 обр., кДж/моль	S°298, Дж/моль×К
NO2	33,5	240,2
N2O4	9,6	303,8

DН°_{298 реакции} = DН°_{298 обр.} ( N₂O₄) - 2×DН°_{298 обр.} (NO₂) = 9,6 - 2×33,5 =

= - 57,4 кДж (- 57400 Дж);

DS°_{298 реакции} = S°₂₉₈ ( N₂O₄) - 2×S°₂₉₈ (NO₂) = 303,8 - 2×240,2 = - 176,6 Дж/К;

DG°_{298 реакции} = DН°_{298 реакции} - Т×DS°_{298 реакции} =

= - 57400 Дж – 298К×(- 176,6 Дж/К) = - 4773,2 Дж.

Так как DG°_{298 реакции} < 0, то при 298К данная реакция возможна в прямом направлении.