Параграф 23. Термодинамическая оптимизация параметров теплоносителей в рекуперативных теплообменных аппаратах.

Для исследования влияния параметров теплоносителей на степень термодинамического совершенства работы рекуперативного теплообменника запишем уравнение прироста энтропии в процессе теплообмена для противотока. В соответствии T-S-диаграммой процесса (рисунок 23.1) изменение энтропии системы определяется изменением энтропии каждого из теплоносителей

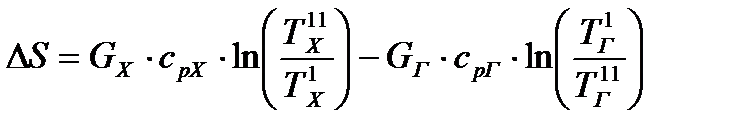. (23.1)

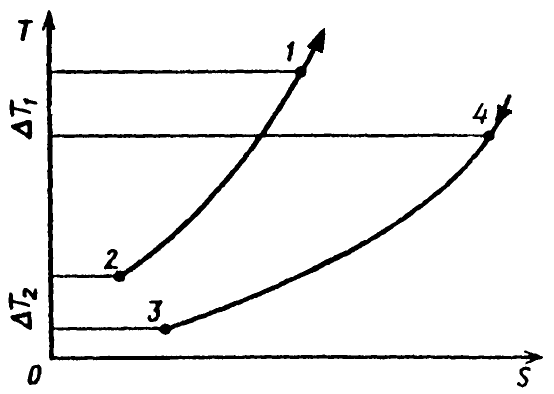
1, 2 ‒ начальное и конечное состояния горячего теплоносителя;

3, 4 ‒ начальное и конечное состояния холодного теплоносителя

Рисунок 23. 1 ‒ T-S- диаграмма процесса теплообмена в

противоточном аппарате

Для простоты расчетов примем G_Г=G_Х, с_рГ=с_рХ=с_р. Тогда

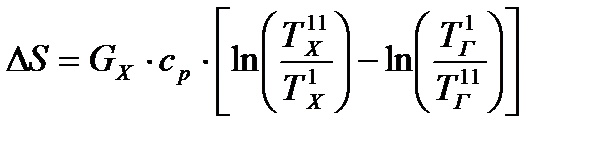. (23.2)

Расход холодного теплоносителя выразим из уравнения теплового баланса

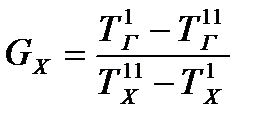. (23.3)

Обозначим 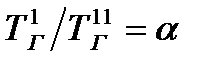; ; 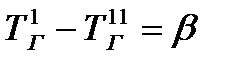; ; 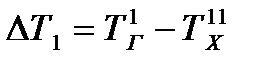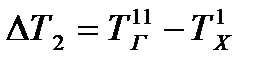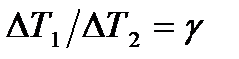. Тогда

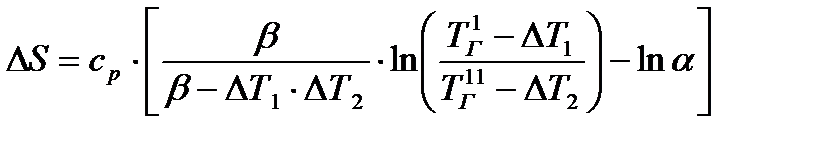. (23.4)

Средняя движущая сила процесса есть средняя логарифмическая разность температур

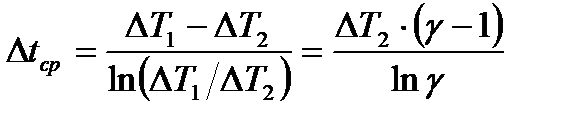, (23.5)

из чего следует

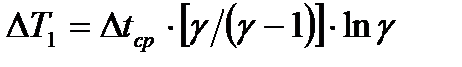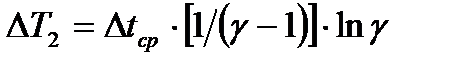; ; (23.6)

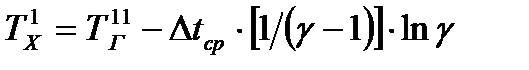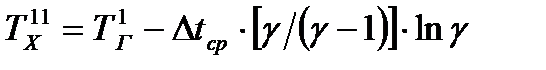; ; (23.7)

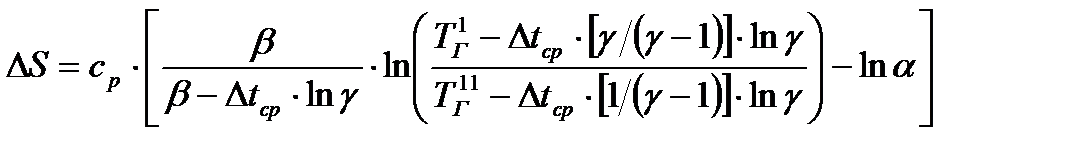. (23.8)

Из последнего выражения видно, что ΔS минимально при 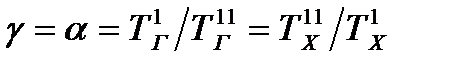. Тогда

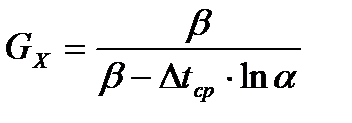. (23.9)

В этом случае прирост энтропии системы в процессе теплообмена и, следовательно, эксергетические потери в аппарате будут минимальны. В соответствии с уравнением Гюи-Стодолы их можно оценить как

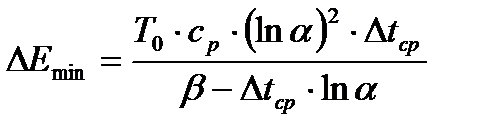. (23.10)

Эксергетический КПД теплообменника при этом будет максимальным

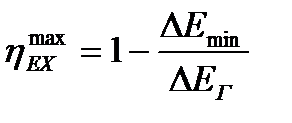, (23.11)

где 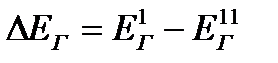‒ уменьшение эксергии теплоносителя, отдающего тепловую энергию в аппарате.

Таким образом, для всех рабочих веществ эксергетические потери будут минимальными при отношении разностей температур теплоносителей на концах поверхности теплообмена, равном отношению граничных температур, т. е. при соблюдении условия

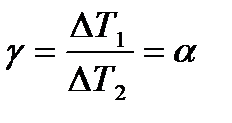. (23.12)

В этом режиме эксергетические потери являются функцией только среднего температурного напора. Любое отклонение от этого условия приводит к увеличению прироста энтропии системы, особенно с повышением среднего температурного напора.

Для случая, когда теплоносителями являются разные вещества с разными давлениями в потоках оптимальные значения температур холодного теплоносителя можно вычислить по уравнению (23.7) с учетом (23.12), а эксергетические потери рассчитать при этих оптимальных температурах.

Минимальное изменение энтропии в противоточном теплообменнике в общем случае зависит от кинетики процесса, теплофизических свойств и температурных характеристик теплоносителей

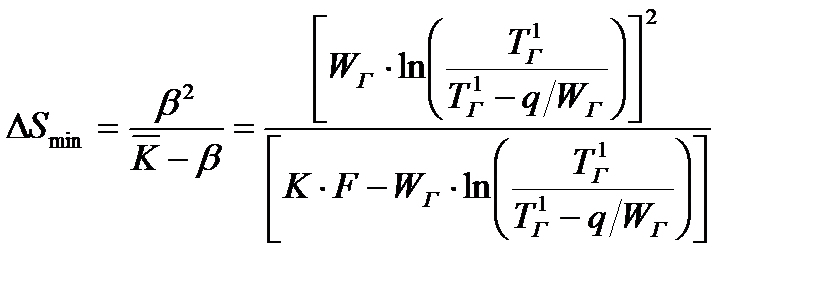, (23.13)

где 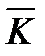, К ‒ соответственно эффективный и средний коэффициенты теплопередачи; F ‒ площадь поверхности теплообмена; ‒ суммарное количество передаваемого в аппарате тепла; W_Г, W_Х ‒ водяные эквиваленты горячего и холодного теплоносителей.

Зависимость минимального изменения энтропии от удельной тепловой нагрузки аппарата носит экстремальный характер (рисунок 23.2).

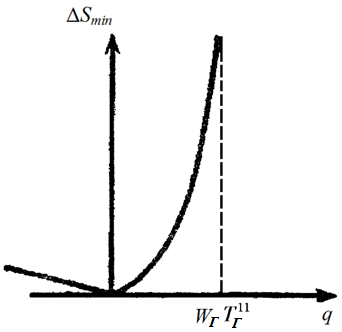
Рисунок 23.2 ‒ Зависимость минимального изменения энтропии от

удельной тепловой нагрузки

На практике, как правило, возникает необходимость в поддержании на постоянном уровне выходной температуры одного из потоков. В этом случае тепловая нагрузка зависит от входной температуры и водяного эквивалента этого потока. Для того чтобы при фиксированной тепловой нагрузке теплообменник работал в термодинамически оптимальных условиях, т. е. с минимальным изменением энтропии, достаточно выполнение равенства

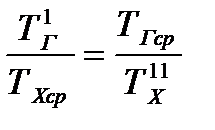. (23.14)

Данное условие характеризует постоянство отношений температур теплоносителей в любом сечении аппарата. В этом случае теплообменник работает в термодинамически оптимальном режиме при любых тепловых нагрузках.

Для оценки термодинамического совершенства работы теплообменника можно использовать показатель энтропийного КПД

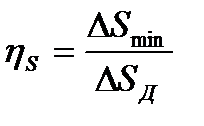, (23.15)

где ΔS_Д ‒ действительное изменение энтропии в теплообменнике.

Если теплообмен протекает в условиях, близких к изобарным, т. е. гидравлическое сопротивление аппарата невелико, то для идеального и большинства реальных газов действительное изменение энтропии определяют по параметрам потоков на входе и выходе теплообменника

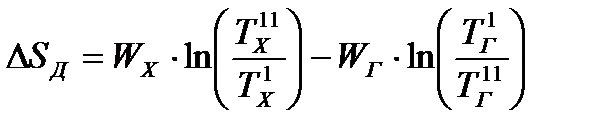. (23.16)

Перераспределяя массовые расходы потоков, можно изменять термодинамическую эффективность работы теплообменника, что отражается непосредственно на водяных эквивалентах потоков. Для приближения параметров процесса к оптимальным значениям устанавливают дополнительные теплообменники на прямом и обратном потоках, используют прием байпасирования потоков, дополнительный подвод теплоносителей и т. д.

Целесообразность использования эксергетического или энтропийного КПД определяется целями проводимого анализа и особенностями работы аппарата. В тех случаях, когда теплообменник является самостоятельным агрегатом и интерес представляет совершенство протекающих в нем процессов, или же когда необходимо сравнить два теплообменника разных конструкций, работающих при одинаковых начальных параметрах, наиболее удобным критерием оценки является энтропийный КПД. Если же теплообменник является частью какой-либо системы и его работу оценивают как работу одного из элементов этой системы с помощью эксергетического КПД.