Параграф 8. Математическое выражение второго закона термодинамики. Энтропия как мера необратимости.

Важнейшим следствием второго закона термодинамики является обоснование существования и свойств такой функции состояния, как энтропия. К понятию энтропии можно прийти различными способами, один из которых основывается на анализе особенностей преобразования теплоты в работу в циклах тепловых двигателей. В соответствии со вторым законом для такого преобразования требуется наличие не только источника, но и приемника теплоты. Если предположить, что температуры источника и приемника постоянны, то единственно возможным циклом, обратимым как внутренне, так и внешне, буде обратимы цикл Карно (рисунок 8.1). Этот цикл состоит из двух внутренне обратимых изотерм с температурами рабочего тела

Т₁ = Т_ИСТ = const и Т₁ = Т_ПР = const (8.1)

соответственно, и двух также внутренне обратимых адиабат. Внешняя обратимость для изотерм обеспечивается соблюдением условия (8.1). Адиабаты из-за отсутствия теплообмена всегда внешне обратимы.

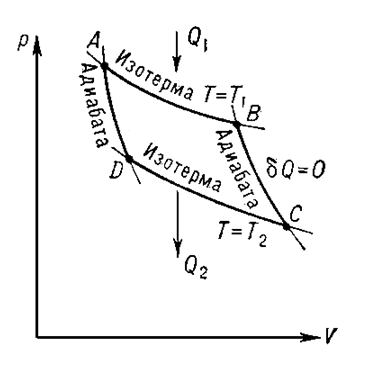
А-В ‒ процесс изотермического расширения рабочего тела;

В-С ‒ процесс адиабатного расширения рабочего тела;

С-D ‒ процесс изотермического сжатия рабочего тела;

D-A ‒ процесс адиабатного сжатия рабочего тела

Рисунок 8.1 ‒ Прямой цикл Карно в координатах p и V

Доля подведенной теплоты, преобразованной в полезную работу в любом прямом обратимом цикле, характеризуется термическим КПД

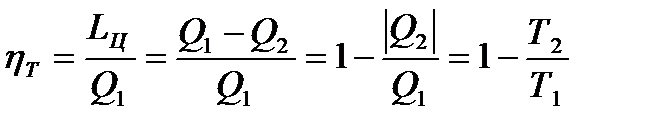, (8.2)

где Q₁ ‒ теплота, отданная источником; Q₂ ‒ теплота, переданная приемнику.

Среди всех других циклов цикл Карно имеет наибольший термический КПД, который не зависит от свойств рабочего тела, а определяется только температурами T₁ и T₂. С учетом этого

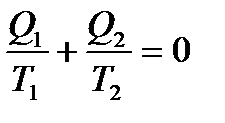. (8.3)

Любой обратимый цикл, протекающий при переменных T₁ и T₂, с математической точки зрения можно представить как совокупность бесконечного числа элементарных обратимых циклов Карно. Для любого обратимого цикла имеем

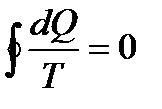. (8.4)

Интеграл по замкнутому контуру равен нулю, когда подынтегральное выражение есть полный дифференциал некоторой функции. В данном случае подынтегральная функция называется энтропией. Ее изменение в любом элементарном обратимом процессе равно

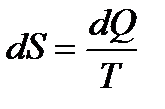. (8.5)

При T=const получаем

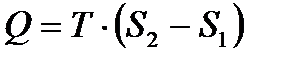. (8.6)

Предположим, что источник теплоты, ее приемник и обратимая машина Карно образуют в совокупности изолированную систему. Энтропия системы будет оставаться постоянной. Для источника и приемника теплоты изменения энтропии соответственно будут равны

,

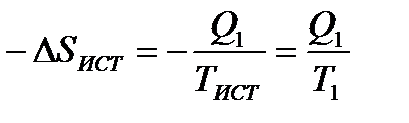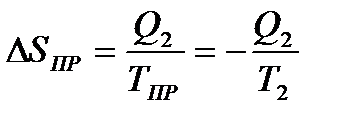, (8.7)

.

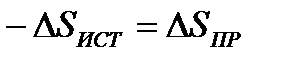Согласно (8.4) энтропия рабочего тела за цикл не меняется, поэтому для всей системы изменение энтропии также равно нулю

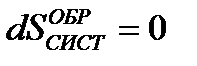. (8.8)

Предположим теперь, что в той же системе машина Карно работает при T_ИСТ>T₁ и T_ПР<T₂, т. е. имеет место внешняя необратимость, которая приводит к потере работоспособности системы. В результате этого термический КПД необратимого цикла будет меньше, чем у соответствующего ему обратимого

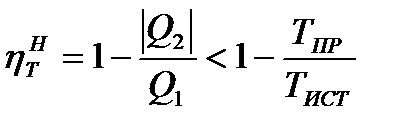. (8.9)

При этом

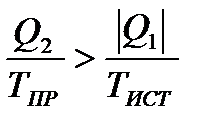. (8.10)

Правая часть неравенства представляет собой уменьшение энтропии источника теплоты вследствие отвода от него теплоты Q₁, а левая ‒ возрастание энтропии приемника вследствие подвода к нему теплоты Q₂. Общая энтропия рассматриваемой изолированной системы в случае необратимого цикла будет возрастать

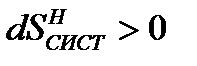. (8.11)

В итоге математическое выражение второго закона имеет вид

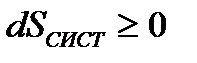. (8.12)

Таким образом, второй закон термодинамики можно трактовать как закон о существовании энтропии и ее неубывании во всех естественных процессах.