Волновой пакет. Соотношения неопределенностей
Итак, в соответствии с гипотезой де Бройля свободной частице с импульсом p
можно поставить в соответствие волну (мы пока ограничимся одномерным случаем)
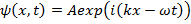 (16.7)
(16.7)
где волновой вектор и частота связаны с импульсом и энергией частицы соотношениями
(16.1), A - нормировочная постоянная. С учетом (5.1) выражение (2.30) можно переписать в виде
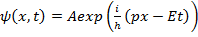 (16.8)
(16.8)
Здесь E и p - энергия и импульс частицы. А как записать энергию частицы, и какую
энергию в (5.1) мы имеем в виду? Для нерелятивистского случая, казалось бы, имеем
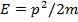 (16.9)
(16.9)
для релятивистской частицы связь энергии и импульса имеет вид
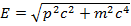 (16.10)
(16.10)
Заметим, что выражение (5.10) не переходит в (5.9) даже в нерелятивистском пределе.
Действительно, разлагая (5.10) в ряд по малому параметру p/mc , получим
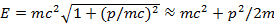 (16.11)
(16.11)
То есть выражение (16.11) содержит по сравнению с (16.9) еще и энергию покоя. Надо ли учитывать энергию покоя при определении частоты волны де Бройля или не надо, заранее не ясно. Оказывается, с физической точки зрения это не имеет существенного значения. Неоднозначность введения частоты волны де Бройля нигде не скажется на физических результатах.
Плоская волна, которую мы связали со свободной частицей, занимает все бесконечное пространство и является нефизическим понятием. Однако из совокупности плоских волн можно составить волновой пакет, локализованный в пространстве
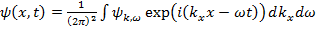 (16.12)
(16.12)
где 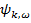 - амплитуды плоских волн, образующих пакет. Можно даже представить себе, что частицы – это и есть локализованные волновые пакеты, перемещающиеся в пространстве и во времени. Такое допущение в принципе возможно, только если скорость перемещения пакета в пространстве совпадает со скоростью движения частицы. Из волновой теории мы знаем, что скорость перемещения пакета как целого определяется так называемой групповой скоростью
- амплитуды плоских волн, образующих пакет. Можно даже представить себе, что частицы – это и есть локализованные волновые пакеты, перемещающиеся в пространстве и во времени. Такое допущение в принципе возможно, только если скорость перемещения пакета в пространстве совпадает со скоростью движения частицы. Из волновой теории мы знаем, что скорость перемещения пакета как целого определяется так называемой групповой скоростью
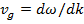 (16.13)
(16.13)
Учитывая, что E = hω, а p = hk , как в релятивистском (5.10), так и в нерелятивистском (5.9) случаях мы получаем
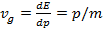 (16.14)
(16.14)
т.е. скорость частицы. Таким образом, пакет действительно перемещается в пространстве со скоростью, равной скорости движение частицы. Однако, различные спектральные компоненты пакета движутся с разными фазовыми скоростями. Например, если мы используем нерелятивистскую связь энергии и импульса (5.9), то для фазовой скорости получим
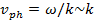 (16.15)
(16.15)
Это означает, что пакет будет расплываться, и, в отличие от электромагнитных волн, для
волн де Бройля вакуум является диспергирующей средой. Поэтому предположение о
том, что частицы это сгустки волн де Бройля должно быть отвергнуто.
В 1926 году М.Борн9 предложил другую интерпретацию для волновой функции
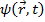 . Согласно Борну, величина квадрата модуля волновой функции |
. Согласно Борну, величина квадрата модуля волновой функции | 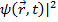 представляет собой плотность вероятности обнаружить частицу в точке с координатой rr в момент времени t. Поэтому саму волновую функцию часто называют амплитудой вероятности. В таком случае расплывание волнового пакета означает, что с течением времени область пространства, в которой может быть обнаружена частица, увеличивается.
представляет собой плотность вероятности обнаружить частицу в точке с координатой rr в момент времени t. Поэтому саму волновую функцию часто называют амплитудой вероятности. В таком случае расплывание волнового пакета означает, что с течением времени область пространства, в которой может быть обнаружена частица, увеличивается.
Как уже отмечалось, пакет (16.12) представляет собой суперпозицию плоских волн, т.е. он характеризуется некоторой шириной спектра. Причем, чем больше размер пространственной области локализации пакета, тем уже его спектр в пространстве вол новых векторов, и, наоборот, узкое пространственное образование можно приготовить, если использовать большой (широкий) набор волновых векторов. Связь ширины спектра с размером пространственной области локализации частицы может быть получена из
(16.12) с помощью обратного преобразования Фурье. Действительно,
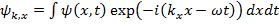 (16.16)
(16.16)
Из (16.16) легко получить, что если волновой пакет ψ(x) характеризуется областью пространственной локализации размером Δx, то ширина спектра волновых векторовΔkx
удовлетворяет соотношению
Δkx Δx≥1 (16.17)
Умножая (16.17) на постоянную Планка, получим
Δkx Δx≥h (16.18)
Здесь величинаΔpx задает ширину пакета 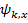 , в пространстве волновых векторов, или,
, в пространстве волновых векторов, или,
что то же самое, в импульсном пространстве. Очевидно, величины Δx и Δpx можно понимать, как неопределенности значений координаты и импульса частицы, состояние которой задается волновой функцией (5.12). В трехмерном случае аналогичные соотношения легко получить и для двух других проекций волнового вектора и координаты:
ΔkzΔz≥h, ΔkyΔy≥h
(16.19)
Мы приходим к важному выводу: координата частицы и ее импульс (речь идет о проекциях на одну и ту же ось) не могут быть заданы со сколь угодно высокой точностью.
Точность их одновременного определения ограничивается соотношениями (2.41), (2.42).
Из сказанного следует очень важный вывод. Постановка задачи о движении частицы в классической механике (по начальным значениям координаты и скорости (или импульса) определить значения этих величин в любой наперед заданный момент времени) оказывается невозможной с точки зрения квантовой теории. Соотношения неопределенностей Гейзенберга не позволяют в принципе задать начальные условия так, как это делается в классической теории. Отсюда в частности следует, что у квантового микрообъекта не может быть траектории. Состояние такого микрообъекта описывается волновым полем, ψ - функцией. Задание этого поля целиком и полностью описывает систему, вся информация, которую мы можем узнать о системе, содержится в ее волновой функции.
Соотношения (16.18), (16.19) в квантовой теории были впервые сформулированы
В.Гейзенбергом10 и носят названия соотношения неопределенностей для импульса и координаты. Отметим, что эти соотношения не накладывают никаких ограничений на точность определения, скажем, x – проекции импульса и y – проекции координаты.
Аналогично соотношениям (16.18), (16.19) из выражений (16.12), (16.16) легко получить еще одно соотношение, устанавливающее связь между временной длительностью
процесса τ и шириной его частотного спектра
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 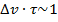 (16.20)
(16.20)
Умножая на h , получаем соотношение неопределенностей Гейзенберга для энергии –
времени:
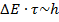 (16.21)
(16.21)
Физическая трактовка этого соотношения заключается в следующем. Если квантовая
система живет некоторое время τ , то энергия этой системы не может быть определена с
точностью лучшей, чем позволяет соотношение неопределенностей
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 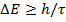 (16.22)
(16.22)
Здесь ΔE - точность определения энергии системы. Мы видим, что теоретически точно измерить энергию у системы можно лишь в том случае, если эта система живет бесконечно долго.
Фактически, соотношение неопределенностей энергия – время устанавливает принципиальные ограничения на точность экспериментальной проверки закона сохранения энергии. Если в системе на некоторое время τ появится дополнительная энергия ΔE , но так, что выполнено соотношение (16.22), то говорить о нарушении закона сохранения энергии нельзя, так как такое нарушение не может быть обнаружено ни в каких экспериментах в принципе.
В заключение отметим, что соотношения неопределенностей представляют собой фундамент квантовой теории. Использование этих соотношений часто позволяет качественно анализировать различные физические ситуации, не прибегая к точному решению задачи.
Опыт Юнга
До открытия принципа корпускулярно-волнового дуализма света среди ученых не было единого мнения о его природе. Одни утверждали, что свет – это поток частиц, корпускул, которые позже назвали фотонами. С развитием науки появилась теория о волновой природе светового излучения. Впоследствии открылось, что оба варианта верны. Свет ведет себя и как поток частиц, чему существует множество подтверждений, таких как фотоэффект или эффект Комптона. Так и как волна, доказательством чему является дифракция и интерференция.
Уже в 1803 году Томас Юнг провел знаменитый эксперимент, который приблизил науку к разгадке феномена.
Эксперимент достаточно прост. Имеется источник света. За ним Юнг использовал экран А, с узкой щелью. После прохождения света от источника через эту щель его можно считать точечным. За первым экраном расположен второй – экран B, уже с двумя щелями, расположенными рядом друг с другом на расстоянии d. Для наблюдения интерференции, необходимо, чтобы источники интерферирующих волн были когерентными. Поскольку изначально свет в эксперименте поступает от одного источника, то проходя через два отверстия экрана B мы получаем два источника когерентного света S1 и S2, т.е. сами щели. Этот метод называется методом деления волнового фронта. Свет этих источников интерферирует, результат можно наблюдать на экране Э.
Что мы ожидаем увидеть на этом экране, исходя из корпускулярной теории света? Наверное, ничего, поскольку можно ожидать, что частицы, двигаясь прямолинейно, пройдут сквозь отверстие первого экрана и образуют пятно света между двумя отверстиями второго. Или, если бы первый экран отсутствовал, то можно было бы говорить о двух полосах света на экране Э. Так бы и случилось, будь прорези в экранах достаточно широкими. Но, что же увидел Юнг? В области, где волны перекрываются, образуется чередование полос с максимумом и минимумом интенсивности света. Причем, максимум яркости окажется там, где согласно корпускулярной теории, яркость должна быть практически нулевой.
Интенсивность в произвольной точке P экрана, лежащей на расстоянии x от нуля, определяется оптической разностью хода дельта, т.е. разницей между расстояний S2 и S1 от вторичных источников света до самой точки P. Используя геометрию, учитывая расстояние l между экранами B и Э, рассчитываем дельта для вакуума. Отсюда находим расстояния X для максимумов и минимумов интенсивности, где лямбда – длина волны. И расстояние дельта X – между соседними максимумами и минимумами. Нужно заметить, раз эта величина обратно пропорциональна расстоянию между щелями d, то при его увеличении, приближении к расстоянию между экранами l, отдельные полосы становятся неразличимыми. Интересно также заметить, что измеряя дельта Х мы можем вычислить длину волны света – лямбда.
Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы. Главный максимум будет соответствовать m=0 и будет находиться центре, а далее, в разные стороны будут чередоваться максимумы первого, второго порядков и т.д.
Итак, мы видим, что свет ведет себя как волна. Но напомню, что это происходит только если ширина отверстий сравнима с длиной его волны. Когда ширина прорезей увеличивается, освещенность экрана уменьшается и интерференции исчезают.
