Параграф 17. Эксергетический анализ сложных ЭХТС.

ЭХТС представляет собой комплекс взаимосвязанных технологических и энергетических устройств, в котором изменение термодинамического совершенства процессов, протекающих в любом из элементов, приводит к изменению показателей термодинамического совершенства ЭХТС в целом.

В ЭХТС структура потоков эксергии оказывается весьма сложной. Потоки эксергии могут поступать извне одновременно в несколько элементов. Часть потоков эксергии внутри системы оказываются замкнутыми вследствие циркуляции вещества и регенерации теплоты.

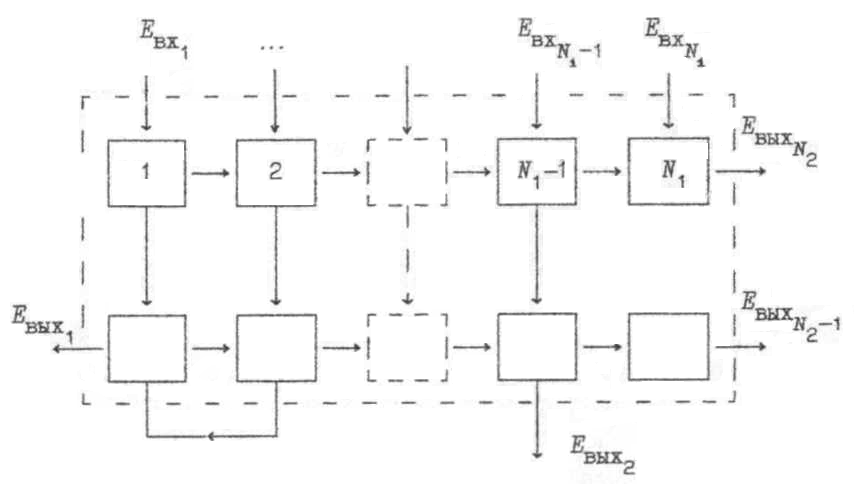
Рисунок 17.1 ‒ Обобщенная схема ЭХТС

Для того, чтобы получить зависимость между показателями термодинамического совершенства отдельных элементов и ЭХТС в целом, рассмотрим ее обобщенную схему (рисунок 17.1). Сплошными линиями со стрелками на схеме показаны потоки эксергии.

Среди общего числа N₀ элементов системы всегда могут быть выделены N₁ головных элементов, через которые в систему поступают потоки эксергии, и N₂ концевых элементов, через которые потоки эксергии уходят из ЭХТС. Через систему могут также проходить транзитные потоки эксергии. Суммарный транзитный поток каким-либо образом распределен, с одной стороны, между элементами, через которые эксергия поступает в систему, и, с другой стороны, между элементами, через которые эксергия из системы отводится. В соответствии с определением эксергетического КПД имеем для всей ЭХТС

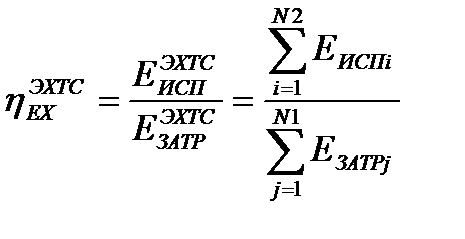, (17.1)

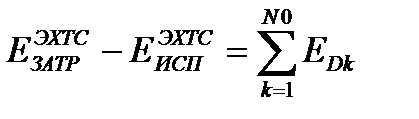, (17.2)

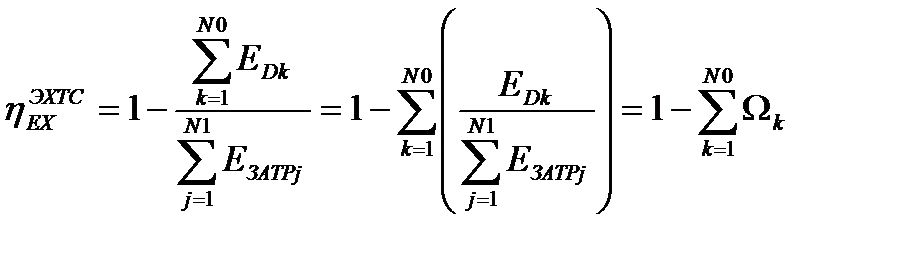. (17.3)

Потери в k-ом элементе ЭХТС равны 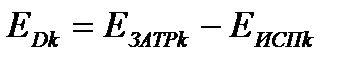. Тогда

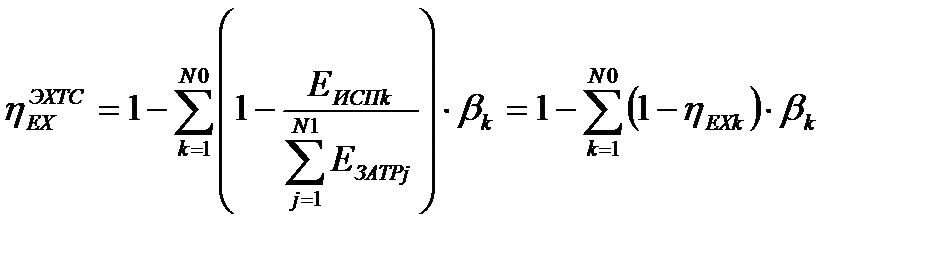, (17.4)

где 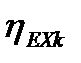‒ эксергетический КПД k-ого элемента, а коэффициент

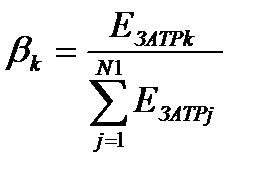(17.5)

выражает отношение эксергии, затраченной в k-ом элементе, к эксергии, затраченной во всей ЭХТС.

Для головных элементов . С учетом этого

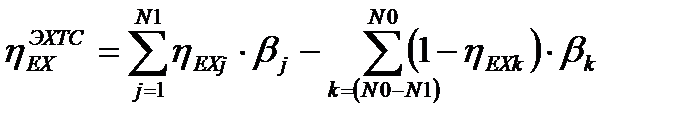. (17.6)

Таким образом, влияние эксергетического КПД элемента на эксергетический КПД системы зависит от того, какую долю составляет эксергия, затрачиваемая в данном элементе, по отношению к общей затраченной в системе эксергии. Количественно указанное влияние определяется коэффициентом .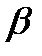

Для оценки эксергетического КПД ЭХТС, отнесенного к производству конкретного вида продукции, можно воспользоваться формулами (17.5) и (17.6), рассматривая только элементы системы, связанные с производством данного продукта.

В частном случае эксергетический КПД ЭХТС может быть выражен как произведение эксергетических КПД элементов

. (17.7)

Однако этой формулой можно пользоваться только при соблюдении следующих условий:

‒ транзит эксергии через систему отсутствует;

‒ вся затраченная эксергия поступает извне только в один из элементов системы;

‒ внутри системы поток эксергии последовательно проходит через все элементы системы от первого до последнего, из которых отводится в виде полезной эксергии.

При соблюдении указанных условий диаграмма Грассмана-Шаргута имеет линейную структуру.