Ошибки прямых равноточных измерений

Измер-я бывают прям и косвен. При прямых измер-х числов знач измер-й велич получ-ся сразу из показаний прибора или при пом метода выполн-го измер-я. Рез-т каждого прямого измер-я вкл случайн ошибку, кот зав от случайных ф-ров. Если абсол велич ошибки меньше чувствит-ти прибора, то они не обнаруж-ся и прибор при многокр измер-х будет показ-ть одно и тоже измер-е, хотя ошибка ≠ 0. В таких случ за велич случайн ошибок приним-ся: 1. Цена наим деления шкалы прибора; 2. Половина цены деления шкалы прибора; 3. Десятая доля наим цены деления прибора.

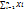Теория ошибок рассм 2 сов-ти случайн величин: Генеральн сов-ть случайн величин Хi <X1, X2, X3, …,Xn…∞> ; µ= = lim ; Ei = µ-X1. Формула Гавса f(Xi; ᵟ)= * l 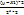; f fmax= (µ-Xi=0); Дисперсия( ср. квалр. ошибка): ᵟ² = =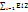

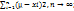
ᵟ- стандарт откл, ᵟ = , n→∞;

Выборочн сов-ть случайн величин Xi. <X1, X2, X3, …,Xn>. Степень свободы f=n-1. ; Хср= 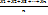= 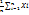; Ei=Xcp – Xi; Дисперсия S² : S^{2= = ;}

S = 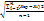, абсолют ошибка E₂=t2×Sxср;

Хср – ср арифм из рез-тов, получ-х при всех измен-х n, яов наиб вероятн и наилучшим значением измер-мой велич. Воспроизвод-ть случайн велич хар-ся Ei=µ-Xi. Наиб вер-ть достиг-ся для Ei=0. Зная ср квадратич ошибку S устан-ть интервал знач, кот приним измеряемая велич. Этот интервал наз-ся доверительным интервалом. Вер-ть того, что новое значение измен величины попадет в доверит интервал наз доверит вер-тью, надежностью или коэф надежн-ти. Итог: для хар-ки случ ошибки, ее учета, необх задавать 2 числа: величину самой ошибки (доверит интервал) и величину доверит вер-ти. P(Xср- E_0.95‹1‹Xi‹Xср+ Е_0.95) = α_0.95)

29.Основ цель рентгеноструктурного анализа(Р.А) кристаллов закл-ся в том, чтобы путем соотв-го рассмотрения картины рассеяния рентг лучей получить изоб-е структуры, рассеивающей рентг лучи. Эта задача решается в два этапа: сначала измеряют интенсивности излучения, рассеянного объектом, после чего путем преобразования картины рассеяния получают изображение. В аналогичном оптическом случае, когда объект, рассеивающий свет, наблюдают с помощью микроскопа. 2-м аспектом Р.А. кристаллов явл прецизионное измерение межатомных расстояний и углов между направлениями химических связей.Из изложенного следует, что рентгеноструктурный анализ кристаллов далеко не всегда дает правильное представление о строении соответствующих индивидуальных молекул или ионов.Закон Брэгга Вульфа определяет зависимость угла отраж-я рентг лучей(α) от длины волны излучения(λ) и межплоск-го расстояния, от кот-го происх отражение,-явл-ся основным законом дифракции рентг лучей в кристалле.Если исп-ть монохроматич изл-е, тоЗ.Брегга Вульфа м/записать:2 d/n sin α=λ, где n- порядок отражения.

Метод Лауэ.

В этом методе неподвижный монокристалл освещается пучком полихроматического (белого) рентгеновского излучения, при этом каждая атомная плоскость, характеризующаяся своим специфическим расстоянием между атомными плоскостями (при постоянном угле падения рентгеновского излучения), отражает лучи определенной длины волны.Рентгенограмма, снятая по методу Лауэ, называется лауэграммой. При съемке лауэграммы пучок рентгеновского излучения падает на кристалл и дифрагированное излучение дает на пленке, перпендикулярной первичному пучку, систему пятен, соответствующих отражениям лучей с различной длиной волны от различных плоскостей. Расположение пятен зависит от кристаллической структуры кристалла и его ориентировки по отношению к первичному пучку лучей.Пятна на лауэграмме образуют эллипсы и гиперболы, проходящие через центр лауэграммы, такое расположение аналогично получаемому при падении луча видимого света на зеркало, расположенное под углом к лучу. Если поставить перпендикулярно падающему лучу экран, на который падает отраженный луч, и поворачивать зеркало относительно оси, лежащей в его плоскости, то луч отраженного света движется по конической поверхности и его пересечение с экраном даст эллипс или гиперболу..В методе вращения кристалла съемка ведется в характеристическом рентгеновском излучении и кристалл вращается вокруг оси, перпендикулярной первичному пучку. Пленка располагается на цилиндрической поверхности, ось которой совпадает с осью вращения кристалла. Кристалл в рентгеновской камере устанавливается так, чтобы кристаллографическое направление с высокой плотностью расположения атомов совпадало с осью вращения. Вместо вращения образец можно поворачивать вокруг той же оси в возвратном режиме (метод качания).Метод вращающегося кристалла и его видоизменения являются наиболее точными и универсальными при определении кристаллических структур.Достоинств метода вращающегося кристалла является то, что измерение расстояния между нулевой и первой слоевыми линиями позволяет сразу найти угол 0 и, следовательно, параметр элементарной ячейки с. Получив рентгенограммы вращения, когда вертикальными являются остальные оси кристалла, можно найти все три параметра элементарной ячейки. Зная размеры ячейки и плотность кристалла, можно легко вычислить число молекул, присутствующих в каждой элементарной ячейке. Часто из одних только параметров элементарной ячейки можно извлечь ценные сведения.

Видоизмененный ( Поляки, 1920) метод вращающегося кристалла используется и теперь. Из пучка рентгеновских лучей, испускаемых антикатодом А, при пропускании через отверстие В в свинцовых пластинках вырезается параллельный луч, который затем отражается кристаллом С, медленно вращающимся вокруг одной из своих кристаллографических осей. Изображения образуются на круглой пленке FEDG только при тех положениях кристалла, когда угол а удовлетворяет уравнению Вульфа - Брэгга.

Большинство исследований структур проведено с помощью метода вращающегося кристалла.

Если от данного кристалла получить три рентгенограммы, соответствующие вращению вокруг трех наиболее простых направлений в кристалле, то таким путем могут быть определены три ребра элементарной ячейки. Метод вращающегося кристалла широко применяется и для полного определения структур, но соответствующая аппаратура и самый ход расшифровки рентгенограмм значительно сложнее.

31.Дифрактометр (Д.)- прибор для измерения интенсивности и направления рент излучения, дифрагированного на кристаллическом объекте. Д. применяется для решения различных задач рентгеновского структурного анализа. Он позволяет измерять интенсивности дифрагированного в заданном направлении излучения с точностью до 10-х долей процента и углы дифракции с точностью до 10-х долей минуты. С помощью Р. д. можно производить фазовый анализ поликристаллических объектов и исследование текстур, ориентировку монокристальных блоков, получать полный набор интенсивностей отражений от монокристалла, исследовать структуру многих веществ при различных внешних условиях и т.д.

Д. состоит из источника рентгеновского излучения, рентгеновского гониометра , в который помещают исследуемый образец, детектора излучения и электронного измерительно-регистрирующего устройства. Детектором в Д. служит не фотоплёнка, как в рентгеновской камере, а счётчики квантов (сцинтилляционные, пропорциональные, полупроводниковые счётчики или Гейгера - Мюллера счётчики). Дифракционную картину образца в Д. получают последовательно: счётчик перемещается в процессе измерения и регистрирует попавшую в него энергию излучения за определённый интервал времени. По сравнению с рентгеновскими камерами Д. обладают более высокой точностью, чувствительностью, большей экспрессностью. Процесс получения информации в Д. может быть полностью автоматизирован, поскольку в нём отсутствует необходимость проявления фотоплёнки, причём в автоматическом Д. прибором управляют ЭВМ, полученные данные поступают на обработку в ЭВМ. Универсальные Р. д. можно использовать для различных рентгеноструктурных исследований, заменяя приставки к гониометрическому устройству. В больших лабораториях применяются специализированные дифрактометры, предназначенные для решения какой-либо одной задачи рентгеноструктурного анализа.