Аконы физико-химического равновесия для реальных систем. Методы определения активности.

екция №7

В реальных системах необходимо учитывать собственный объем частиц и их взаимодействие до столкновения. Степень этого взаимодействия изменяется с изменением состава раствора, в результате чего эффективные концентрации компонентов отличаются от «валовых» концентраций, определяемых химическим анализом. В качестве упрощенного примера можно привести случай, когда кремнезем в шлаке образует химическое соединение 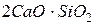, а кремний в металле – соединение 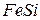, которые лишь частично диссоциированы. В этом случае для реакции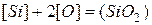

,

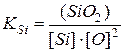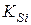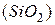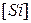где – константа равновесия, в которой учитывается общая («валовая») концентрация и не будет постоянной величиной при данной температуре, а будет зависеть также от состава шлака и металла.

Применительно к реальным системам вводится понятие активности компонента 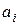, которая характеризует стремление его выделиться из раствора, а также относительную его способность реагировать с другими веществами. Активность – это кажущаяся концентрация компонента реального раствора, определяющая его термодинамические свойства, с учетом взаимодействия растворенного компонента с другими компонентами раствора. Если в уравнениях констант физико-химического равновесия вместо концентраций компонентов учитывать их активности, то обеспечивается постоянство констант при постоянной температуре.

Поскольку активность компонента 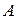характеризует его способность выделяться из раствора, то она пропорциональна парциальному давлению насыщенного пара компонента или его активности в другой конденсированной фазе, равновесной с изучаемым раствором:

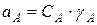(2.11)

где 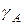– коэффициент активности компонента 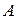в растворе, учитывающий отклонение свойств компонента в реальной системе от его свойства в идеальной системе. Обозначение активности вещества 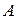в растворе: 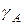– концентрированном, 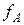– разбавленном.

Коэффициент активности является количественной характеристикой отличия реального раствора от совершенного при той же концентрации компонентов, которое более заметно проявляется при небольших концентрациях и уменьшается по мере их увеличения.

Константы равновесия и распределения в реальных системах сохраняют постоянство при постоянной температуре, если вместо концентраций подставить активности:

уравнение закона действия масс 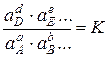(2.12)

закон распределения Нернста 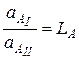(2.1耳)

закон Генри 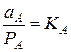(2.14)

закон Рауля 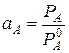(2.15)

Таким образом, в реальных системах константа равновесия представляет собой соотношение произведений равновесных активностей продуктов реакции и реагентов, которые отражают соотношение скоростей обратной и прямой реакции при равновесии.

Состояние компонента с активностью 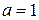называется стандартным.

Выбор стандартного состояния диктуется удобствами расчетов или наличием достаточно надежных экспериментальных данных. Чаще всего в качестве стандартного состояния выбирают чистый компонент, насыщенный или разбавленный раствор (1%-й). Коэффициент активности компонента может быть больше единицы, а активность – больше концентрации (в зависимости от стандартного состояния, при котором 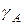и 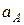принимают равными единице). Так, если в растворе 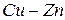за стандартное состояние принять 1%-й раствор 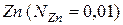(см. рис. 2.1), то идеальный закон Генри соблюдается при 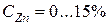(масс.)¹. При 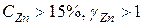и . 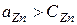Например, пр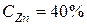и и 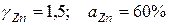(положительное отклонение от закона Генри). Если за стандартное состояние принять чисты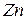й (при 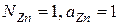), то идеальный закон Рауля соблюдается при 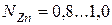. 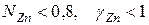При и 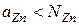. Например, при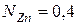

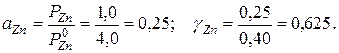
Отрицательные отклонения от идеального закона Рауля обусловлены взаимодействием между частицами (взаимным притяжением с выделением теплоты). Возможны и положительные отклонения (при взаимном отталкивании частиц).

Существует прямая зависимость между активностью компонента в растворе и его химическим потенциалом (парциальным молярным изобарно-изометрическим потенциалом в растворе):

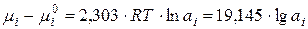(2.16)

где 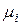, 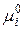– химический потенциал компонента соответственно в растворе и в стандартном состоянии, в котором .

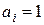Активность компонентов металлического расплава

В реальных растворах способность компонента переходить в пар или вступать в химическую реакцию, как правило, не определяется только концентрацией. Это проявляется в отклонениях от закона Рауля (давление пара каждого из компонентов прямо пропорционально его мольной доле 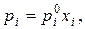) и Генри (Давление пара растворенного вещества прямо пропорционально его концентрации 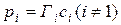), а также в том, что константы реакции с участием растворов, выраженные через отношения концентраций, не остаются постоянными при переходе от одних концентраций к другим. Причиной таких отклонений является взаимодействие компонента с остальными веществами, находящимися в растворе. Количественной характеристикой, учитывающей как концентрацию, так и взаимодействие компонента с другими веществами в растворе, является его активность. В общем виде под активностью понимают отношение парциального давления пара компонента над раствором р_i к аналогичной величине для стандартного состояния компонента 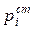Очевидно, что в стандартном состоянии активность равна 1. Если рассматривают отклонения от закона Рауля, то за стандартное состояние принимают чистый компонент. В этом случае активность (обозначим ее 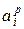) определяют выражением:

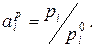(1.1)

Связь между определенной таким образом активностью и мольной долей выражают соотношением:

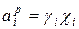(1.2)

где 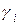- коэффициент активности. Если соблюдается закон Рауля, то, как видно из уравнений (1.1) и (1.2), 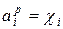. В этом случае g_i=1. При отрицательных отклонениях от идеальности g_i<1, при положительных отклонениях g_i>1. Таким образом, коэффициент активности g_i количественно характеризует отличие реального раствора от совершенного при той же концентрации.

Наряду с рассмотренным способом определения активности существует другой способ, в котором объектом описания являются отклонения не от закона Рауля, а от закона Генри. Стандартным состоянием компонента в этом случае является идеальный разбавленный раствор единичной концентрации (при этом обеспечивается равенство 1 активности в стандартном состоянии).

Расчет коэффициентов активности компонентов в сложном металлическом расплаве

Активность компонента В в растворе А-В, где А является растворителем, обычно изменяется при добавлении в раствор других компонентов (С, Д и т.д.). В сложном растворе коэффициент активности g_в будет зависеть от природы компонентов раствора:

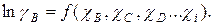(1.3)

Для учета влияния всех компонентов раствора на активность рассматриваемого компонента привлекают понятие параметров взаимодействия, которые определяются из выражения, получаемого при разложении в ряд Тейлора избыточной свободной энергии 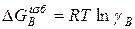около точки, близкой к чистому растворителю:

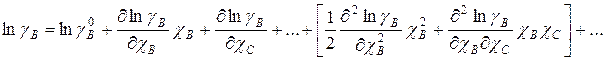. (1.4)

Производные 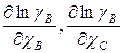и т.д. называют параметрами взаимодействия первого порядка. В общем случае их обозначают:

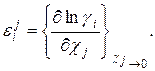(1.5)

Производные 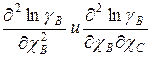называют параметрами взаимодействия второго порядка и в общем случае:

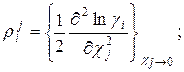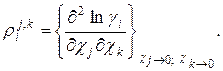(1.6) (1.7)

С учетом принятых обозначений (1.5)-(1.7) выражение (1.4) принимает вид:

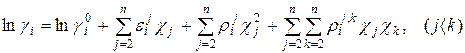
(1.8)

Таким образом, для сложного расплава А-В-С-Д- … параметры взаимодействия первого порядка показывают влияние добавленных компонентов (С, Д и т.д.) на коэффициент активности рассматриваемого компонента (В). Параметры взаимодействия второго порядка показывают характер изменения параметра взаимодействия первого порядка ( 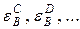) под влиянием увеличения концентрации других компонентов (С, Д и т.д.) в расплаве.

Обычно более удобно за стандартное состояние принять 1%-ный раствор компонента i в расплаве и использовать десятичные логарифмы вместо натуральных. Тогда первое слагаемое исключается, поскольку 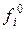=1 и 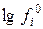=0, а выражение (1.8) принимает вид:

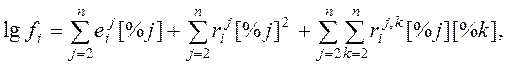(1.9)

где фигурируют другие параметры взаимодействия первого и второго порядка:

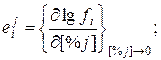(1.10) 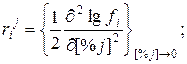(1.11) 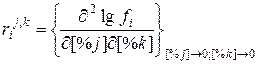(1.12)

При невысоких концентрациях растворенных компонентов (С, Д, и т.д.) слагаемыми, включающими параметры взаимодействия второго порядка, можно пренебречь. Тогда выражение (1.8) упрощается:

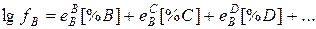(1.13)

Между параметрами взаимодействия установлены следующие соотношения:

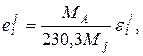(1.14)

где М_А и М_J атомные массы металла-растворителя и компонента j.

В частности, для растворов в железе:

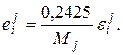(1.15)

Между так называемыми “перекрестными” параметрами взаимодействия существует простая связь:

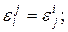(1.16) 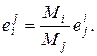(1.17)

Для бинарных растворов А-i, где А-растворитель, а i-растворенное вещество при низкой концентрации

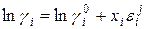(1.18)

Пользуясь основными соотношениями для параметров взаимодействия, можно находить значения коэффициентов активности компонентов в сложных многокомпонентных расплавах.

Значения параметров взаимодействия 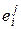для растворов различных веществ в жидком железе при 1600 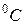приведены в таблице 1.

Параметры взаимодействия 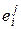зависят от температуры расплава. Эта зависимость имеет вид:

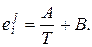(1.19)

Таблица 1.Параметры взаимодействия первого порядка

для растворов С, Н, N, О и S в жидком железе при 1600 ⁰С

Элемент, Х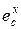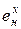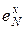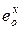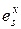
Al	0,043	0,013	–0,028	–3,9	0,035
B	0,24	0,05	0,094	–2,6	0,13
C	0,14	0,06	0,13	–0,13	0,11
Co	0,008	0,002	0,011	0,008	0,003
Cr	–0,024	–0,002	–0,047	–0,04	–0,011
Cu	0,016	0,001	0,009	–0,013	–0,008
Mn	–0,012	–0,001	–0,002	–0,021	–0,026
Mo	–0,008	0,002	–0,011	0,004	0,003
N	0,11	–		0,057	0,01
Nb	–0,06	–0,002	–0,06	–0,14	–0,013
Ni	0,012		0,01	0,006
O	–0,34	–0,19	0,05	–0,20	–0,27
P	0,051	0,011	0,045	0,07	0,29
S	0,046	0,008	0,007	–0,133	–0,028
Si	0,08	0,027	0,047	–0,131	0,063
Sn	0,041	0,005	0,007	–0,011	–0,004
Ti	–	–0,019	–0,53	–0,31	–0,072
V	–0,077	–0,007	–0,093	–0,14	–0,016
W	–0,006	0,005	–0,002	–0,009	0,01
Zr	–	–	–0,63	–3,0	–0,052