Расчет температурного поля предельного состояния

Тепловое состояние и распределение температур в свариваемом или нагретом теле характеризуется температурным полем, которое представляет собой совокупность температур всех точек тела в данный момент времени.

Температурное поле есть распределение температур в теле в конкретный момент времени. Оно может выражаться как в абсолютной температуре (Т), так и в приращении температур (ΔТ) по отношению к начальной температуре тела Т_о. В общем случае температурное поле может быть функцией не только координат x, y, z отдельных точек, но и времени t:

Т=(x, y, z, t),(1.3)

Формула описывает объемное температурное поле. Оно может быть плоским T=T(x, y, t) или линейным T(x, t).

Если проследить за изменением температуры точек тела от действия какого–либо источника тепла, то можно выявить закономерности:

1) В начальный момент температуры точек тела повышаются, а температурное поле, изображаемое изотермами, расширяется. Каждая точка нагреваемого тела получает тепла больше, чем отдает. Этот период в нагреве тела называется периодом теплонасыщения.

2) По истечении времени количество тепла, отдаваемого каждой точкой другим точкам, становится равным вводимому количеству тепла. Вследствие чего температура точек не изменяется, и температурное поле остается неизменным во времени. Этот период называется предельным состоянием или стационарным.

3) С момента прекращения действия источника тепла, в теле происходит перераспределение введенного тепла. Температура точек выравнивается. Этот период называется периодом выравнивания температур.

Руководствуясь заданной расчетной схемой подвижного линейного источника тепла в пластине рассчитаем распределение температуры в предельном состоянии вдоль оси Х–Х, совпадающей с линией движения источника тепла, а также линий, параллельных оси Х–Хи отстоящих от нее на расстоянии 0,5; 1; 1,5; 2 см. по формуле (1.4):

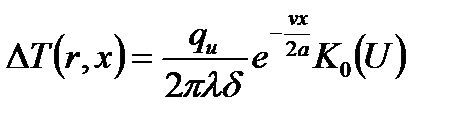(1.4)

где ∆Т – приращение температуры, °С;

r – расстояние от источника до рассматриваемой точки, см;

х – расстояние от места действия источника до точки на линии действия источника до точки на линии действия источника ОХ;

a – коэффициент температуропроводности (для низкоуглеродистых и легированных сталей а=0,08) см/сек;

К₀ – функция Бесселя второго рода нулевого порядка от аргумента U (определяется по таблице см. приложение)

где

,

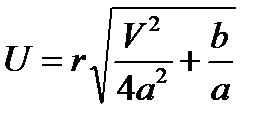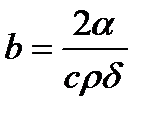– коэффициент температуропроводности, сек^-1;

α =6•10^-3 – коэффициент поверхностной теплоотдачи, Вт/см²•К.

Уравнение (1.4) позволяет определить лишь приращение температуры ∆Т, полное же значение температуры определяется выражением

Т=∆Т+Т₀ (1.5)

где Т₀ начальная температура (в нашем случае Т₀=20 °С).

Рассчитаем коэффициент температуроотдачи:

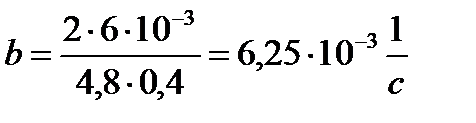
2.1 Расчет распределения температур вдоль оси Х–Х при У=0 см.

Зададимся произвольным значением Х= –2 см (позади источника). Так как Y=0, то

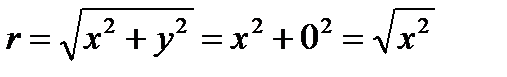. При х= –2см → r=2см.

Рассчитаем аргумент второго порядка U:

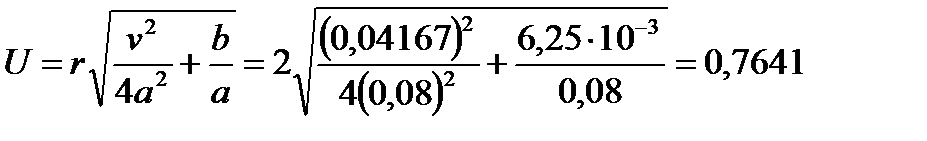К₀(U)= К₀(0,76)=0,60118.

Рассчитаем приращение температуры:

∆Т(2; –2)= 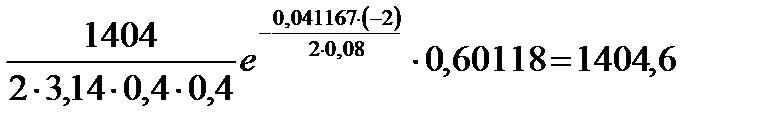°С

Температура в этой точке: Т=∆Т+Т₀=1405+20=1425 °С.

для того, чтобы построить кривые распределения температур на оси Х–Х, возьмем еще по нескольку точек впереди и сзади источника и определим для них температуры, результаты расчетов приведем в таблице 2.1.

Таблица 2.1

х, см	r, см		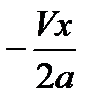	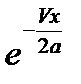U	K0(U)	∆Т, °С	Т=∆Т+Т0
–2		0,521	1,684	0,7641	0,60118
–3		0,78132	2,1844	1,146	0,34586
–4		1б04176	2,8342	1,528	0,20568
–6		1,5626	4,7714	2,292	0,080102
–8		2,08352	8,0327	3,056	0,032415	363,8
–10		2,6044	13,523	3,82	0,01355
–15		3,9066	49,729	5,73	16,486·10–4
–25		6,511	672,499	9,55	2,852·10–5
		–0,26044	0<7707	0,382	1,1596
0,75	0,75	–0,19533	0,8226	0,2865	1,40425
1,5	1,5	–0,39066	0,6766	0,573	0,81814
		–0,52088	0,59399	0,764	0,60118
		–0,78132	0,4578	1,146	0,34586
		–1,04176	0,35283	1,528	0,20568
		–1,3022	0,27193	1/91	0,12727
		–2,08352	0,1245	3,056	0,032793

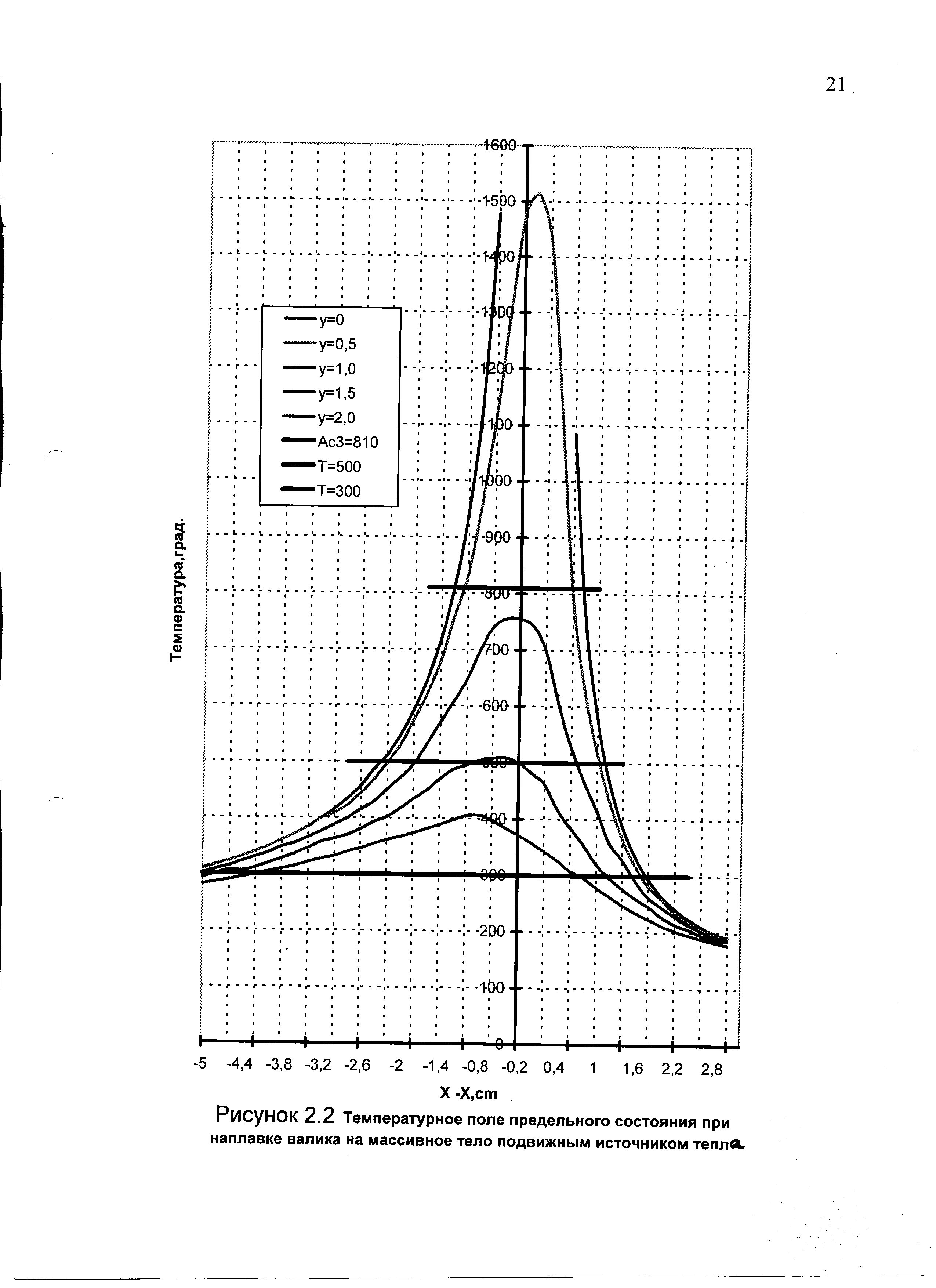
Рисунок 2.1 – Температурное поле предельного состояния при наплавке валика на пластину линейным подвижным источником тепла

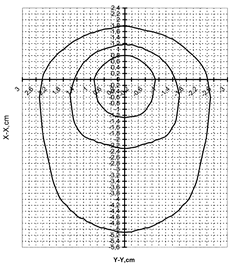
Рисунок 2.2 – Изотермы на поверхности полубесконечного тела

Далее по этой же методике рассчитать распределение температур вдоль оси Х–Х при Y равном 0,5; 1;1,5 и 2 см. Полученные расчетные значения поместить в таблицы.

По полученным расчетным данным построить в масштабе кривые распределения температур в системе координат «Х – Т». Пример графика приведен на рисунке 2.1.