Применение вейвлет-преобразования для обработки дискретных сигналов систем полупроводниковых адсорбционных датчиков

Чежина О.М.

Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики,

Санкт-Петербург, Россия.

Студент VI курса.

[email protected]

Научный руководитель: Эль-Салим С.З.

Обнаружение примесей паров и газов в воздухе, проводимое с применением полупроводниковых адсорбционных датчиков резистивного типа, основано на измерении падения напряжения на газочувствительном элементе при его нагреве до температуры, определяемой подводимой к нагревательному элементу мощностью, регулируемой в диапазоне от 50 до 2000 мВт. Изменение падения напряжения зависит от изменения сопротивления газочувствительного слоя в результате адсорбции молекул примеси исследуемого вещества при прокачке через объем камеры реакций потока воздуха с регулируемым расходом в диапазоне от 0,7 до 2 л/мин. Объем газовой камеры фиксирован и составляет 30 мл, что позволяет проводить обнаружение примесей паров и газов в воздухе в режиме полного перемешивания.

Применение вейвлет-преобразования обусловлено частотно-временной локализацией как аналогового, так и цифрового массива полученной при измерении информации. Разложение спектра по базису вейвлет-образующих функций позволяет раскрыть тонкую структуру спектра в реальном масштабе времени и устранить неопределенность, характерную для Фурье-преобразования. Неопределенность Фурье образа обусловлена принципом Гейзенберга, который не позволяет локализовать высокочастотные составляющие спектра.

В случае измерения напряжения с квантом времени Δt, вейвлет-образ U(t) имеет вид:

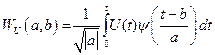(1)

Коэффициенты a и b определяют масштабирование по времени и деформацию вейвлет-производящей функции ψ. В этом случае вейвлет-образ примет вид:

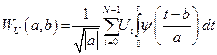(2)

При этом a изменяется от 1 до N, b - от 0 до N-1. Таким образом, сигналу U_i с количеством отсчетов, равных N ставится в соответствие матрица размерностью NxN.

Массив вейвлет-преобразования W_U(a,b) вычисляется при вариации коэффициентов a и b по измеренным значениям U(t) при условии a ≠ 0. Но, учитывая шаг сдвига по времени – 1 с, определенный интерес представляют целочисленные сдвиги b и масштабирующие коэффициенты 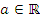. Для сигналов конечной длины выражение (2) представляет собой конечную сумму, которую можно вычислить в масштабе реального времени процесса измерения.

Следует отметить, что для конечных сумм и ограничений, обусловленных схемой измерений, вейвлет-преобразование не является обратимым. То есть, по полученным коэффициентам W_U(a, b) обратное восстановление сигнала до U_i невозможно. В то же время для задачи обнаружения примесей в воздухе с помощью полупроводниковых адсорбционных датчиков при правильном выборе вейвлет-образующей функции восстановление сигнала не требуется.

Таким образом, выбор образующей функции вейвлет-преобразования, позволяет повысить селективность обнаружения аналитической системой с ограниченными физическими параметрами степенями свободы и вывести алгоритм идентификации обнаруживаемого вещества по параметрам, являющимися фундаментальными, такими как, мощность нагрева, каталитическая примесь и материал основы газочувствительного слоя.