Параграф 22. Эксергетический анализ теплообменных аппаратов.

Большинство процессов, протекающих в ХТС, в той или иной степени связано с теплообменом рабочих веществ и теплообменом с окружающей средой. При этом эксергия одного рабочего тела повышается за счет уменьшения эксергии другого, а часть эксергии безвозвратно теряется. Причиной потерь эксергии является увеличение энтропии системы, поэтому для их определения можно использовать уравнение Гюи-Стодолы. Для определения эффективности работы теплообменных аппаратов необходимо оценить эти потери.

Потери от конечной разности температур. При передаче тепла от одного теплоносителя к другому эксергия теплового потока уменьшается на величину

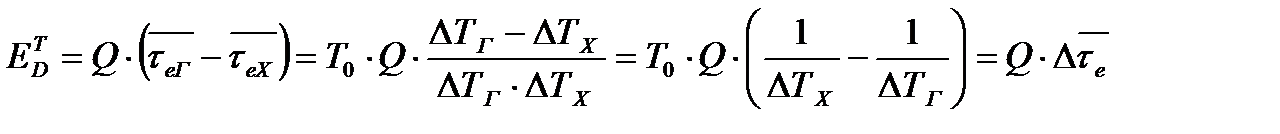, (22.1)

где Q ‒ тепловой поток между теплоносителями; ΔТ_Г, ΔТ_Х ‒ соответственно средние температуры горячего и холодного теплоносителей; 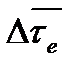‒ средняя разность эксергетических температур теплоносителей.

В процессе теплообмена никакой полезной работы не совершается, поэтому изменение эксергии теплового потока равно потерям, обусловленным необратимостью процесса из-за конечной разности температур теплоносителей. Таким образом, эксергетические потери от конечной разности температур при теплообмене для данного теплового потока пропорциональны средней разности эксергетических температур теплоносителей.

Необратимые потери эксергии в процессе теплообмена вызваны двумя причинами. Первая причина обусловлена неравенством тепловых эквивалентов теплоносителей, участвующих в процессе, что приводит к неодинаковому изменению их температур. Для адиабатного теплоизолированного теплообменника справедливо уравнение теплового баланса

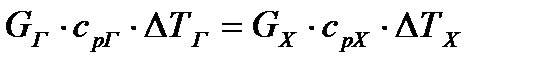, (22.2)

где 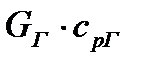, 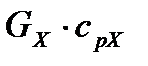‒ тепловые эквиваленты теплоносителей; G_Г, G_X ‒ расходы теплоносителей; с_рГ, с_рХ ‒ средние изобарные теплоемкости теплоносителей.

Поскольку в общем случае тепловые эквиваленты теплоносителей не равны друг другу, то не равны друг другу и средние температуры теплоносителей. В соответствии с уравнением (22.1) это вызывает необратимые потери.

Вторая причина, обусловливающая потери эксергии в процессе теплообмена, ‒ проведение его при фиксированных значениях поверхности теплообмена и коэффициента теплопередачи. Это приводит к тому, что на одном конце поверхности теплообмена минимальная разность температур теплоносителей отлична от нуля. Из-за этого разность их температур во всех сечениях поверхности теплообмена возрастает на определенную конечную величину.

Отметим, что при использовании противоточной схемы движения теплоносителей удается обеспечить более равномерное распределение движущей силы вдоль поверхности теплопередачи.

Потери от гидравлических сопротивлений. Общие эксергетические потери от гидравлических сопротивлений можно представить в виде

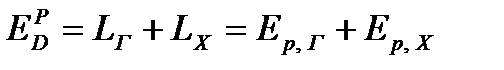, (22.3)

где L_Г, L_Х ‒ работы нагнетательных устройств теплоносителей; Е_{р, Г}, Е_{р, Х} ‒ потери эксергии теплоносителей от гидравлических сопротивлений, рассчитываемые по изменению энтропии как механической составляющей эксергии.

Потери от внешнего теплообмена. Этот вид потерь связан с наличием теплового потока между аппаратом и окружающей средой. Если процесс протекает при Т>T₀, то тепловой поток направлен к окружающей среде, вследствие чего горячий теплоноситель медленнее охлаждается, а холодный медленнее нагревается. Весь поток эксергии, обусловленный внешним теплообменом, безвозвратно теряется и направлен в окружающую среду через тепловую изоляцию

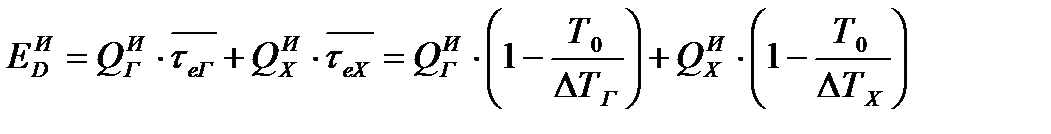, (22.4)

где 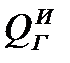, 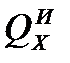‒ соответственно потери теплоты теплоносителей в окружающую среду.

Потери, вызванные продольной теплопроводностью теплообменника. В теплообменнике, в котором температуры теплоносителей изменяются по длине теплообменной поверхности, существует не только тепловой поток, перпендикулярный этой поверхности, но и другой, параллельный ей и направленный от теплой стороны к холодной. Это явление приводит к тому, что фактический, результирующий, вектор теплового потока направлен под острым углом к поверхности, и теплопередача происходит при несколько большей разности температур, чем при отсутствии продольного теплообмена. В результате увеличиваются разности температур на концах теплообменника: холодный теплоноситель выходит более холодным, а горячий теплоноситель более теплым, чем при отсутствии продольного теплообмена. Поэтому потери от продольного теплообмена должны учитываться в составе потерь от конечной разности температур.

В области высоких температур эти потери большей частью относительно невелики, и ими справедливо пренебрегают. В низкотемпературной технике их значение существенно больше, поэтому в криогенных системах находят применение теплообменники, в которых продольная теплопроводность сведена к минимуму (в частности, матричные теплообменники).

При проведении эксергетического анализа основным показателем является эксергетический КПД. В условиях, когда всеми потерями, кроме потерь от конечной разности температур, можно пренебречь, эксергетический КПД теплового потока, участвующего в процессе теплообмена, удобно выражать через отношение величин, характеризующих эксергию теплоносителей. В качестве таких величин можно принять как саму эксергию теплоносителей, так и ее изменение в процессе теплообмена. Тогда для изобарного теплообмена

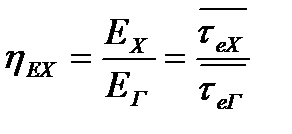. (22.5)

Если гидравлическое сопротивление аппарата значительно, то рассчитанное значение эксергетического КПД может быть отрицательным. Физический смысл этого явления заключается в том, что полученная потоком при охлаждении эксергия оказывается меньше, чем потеря, связанная с проталкиванием его через теплообменник. Но это не доказывает, что процесс невыгоден. Все зависит от того, какую ценность для потребления имеет эксергия того или иного вида. Однако в этом случае целесообразно записать выражение для расчета эксергетического КПД в ином виде

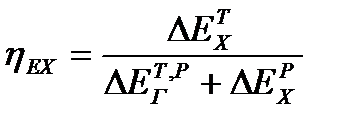, (22.6)

где 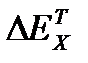, 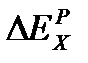‒ изменения эксергии холодного теплоносителя вследствие теплообмена при конечной разности температур и гидравлического сопротивления аппарата соответственно; 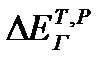‒ изменения эксергии горячего теплоносителя вследствие суммарного влияния этих двух факторов. Эксергетический КПД, рассчитанный этой формуле, всегда положителен и меньше единицы. С его помощью можно изучить зависимость отдельных составляющих потерь эксергии и эффективности процесса теплообмена от технологических параметров: скорости теплоносителей и поверхности теплообмена (рисунок 22.1). В общем случае максимум значения эксергетического КПД не соответствует минимуму эксергетических потерь, так как затраты на реализацию процесса теплообмена включают затраты не только на компенсацию этих потерь, но и на другие эксплуатационные расходы.

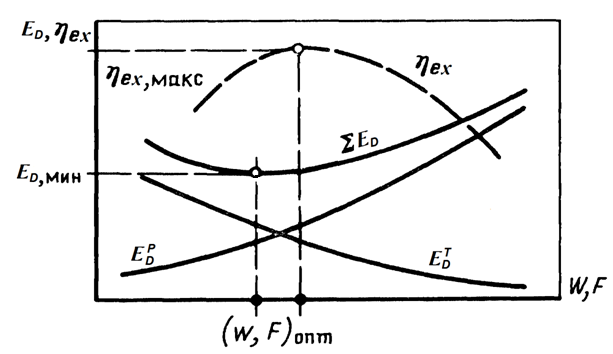
Рисунок 22.1 ‒ Связь между потерями эксергии и

величинами скорости и поверхности теплообменника

Баланс эксергии теплообменного аппарата имеет вид

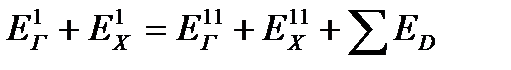, (22.7)

где 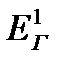, 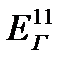‒ эксергии горячего теплоносителя на входе в теплообменник и на выходе из него; 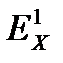, 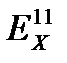‒ эксергии холодного теплоносителя на входе в теплообменник и на выходе из него.

Запишем выражение для расчета эксергетического КПД теплообменника в двух случаях:

1) с учетом транзита эксергии;

2) без учета транзита эксергии, но с учетом внешний потерь.

Для первого случая имеем

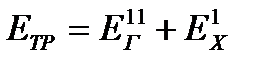; (22.8)

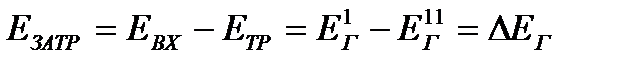; (22.9)

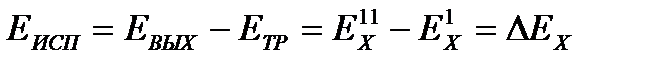; (22.10)

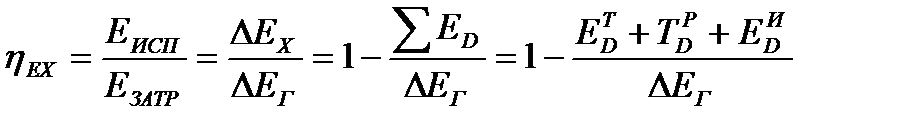. (22.11)

Для второго случая запишем

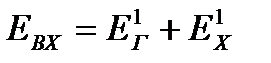; (22.12)

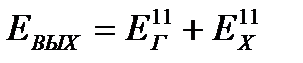; (22.13)

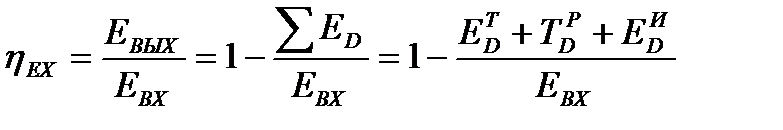. (22.14)

Зависимость потерь эксергии в теплообменнике от параметров теплоносителей, с учетом только термической составляющей их эксергии, может быть выражена из эксергетического баланса

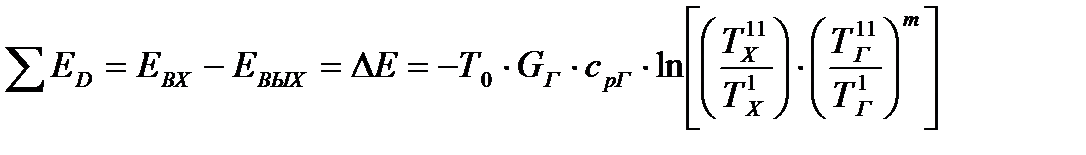, (22.15)

где .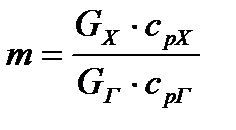

При m<1, т. е. в тех случаях, когда горячий теплоноситель охлаждается сильнее, чем нагревается холодный, потери эксергии выше, чем при m=1. При m>1, когда температура холодного теплоносителя повышается на большую величину по сравнению с уменьшением температуры горячего, потери эксергии в теплообменнике меньше, чем при m=1. Исходя из этого, можно сделать практический вывод о необходимости избегать «перекосов» температур на концах поверхности теплообменника, приводящих к реализации процесса в режиме m<1. Это означает, что нецелесообразно нагревать большие массы веществ небольшим количеством горячего теплоносителя, так как при этом уменьшается его энергетический потенциал.

При смешении рабочих веществ в процессе теплообмена формула для определения потерь эксергии видоизменяется

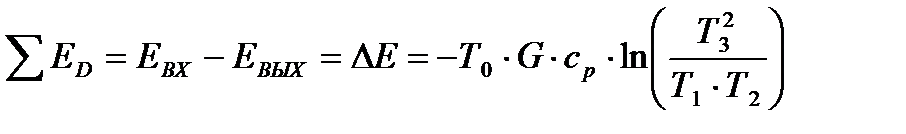, (22.16)

где G, c_p, T₃ ‒ параметры рабочего вещества на выходе из аппарата; Т₁, Т₂ ‒ температуры исходных материальных потоков на входе в теплообменник.

Как правило, после того, как горячий теплоноситель передал часть своей тепловой эксергии холодному теплоносителю и покинул аппарат, в дальнейшем технологическом процессе его эксергия не используется. Поэтому его эксергию на выходе из теплообменника во многих случаях можно отнести к внешним потерям. Эксергетический КПД такого теплообменника равен

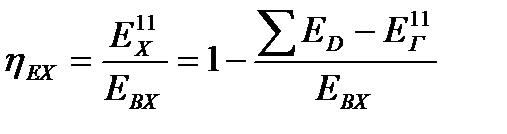. (22.17)

Отметим, что при увеличении поверхности теплопередачи таких теплообменников можно снизить потери эксергии до минимума. В этом случае в аппаратах реализуется ситуация, близкая к обратимому процессу, когда практически весь потенциал эксергетических потерьпереходит в потоки теплоносителей. И получается, что проблема эффективности процесса теплообмена сводится к проблеме утилизации теплоты горячего теплоносителя, которая относится к ВЭР.

Таким образом, эксергетический КПД носит весьма обобщенный характер. Конкретное выражение для него зависит от назначения и особенностей анализируемого процесса и видов взаимодействия потоков. Кроме того, с использованием понятия транзитной эксергии его величина меняется и может быть отрицательной.