Математическое описание ФДЭ.

В соответствии со схемой (1) реакций, идущих при ФДЭ, обозначим: [P] ,[P_s*], [P_T*] - молярные концентрации основного, синглетного и триплетного возбужденных состояний ФС соответственно; [³O₂], [¹O₂*] - то же для основного и синглетного возбужденного состояний молекулы кислорода; k_f и k_q – константы люминесцентного распада состояний S* и T* ФС соответственно; k_r - константа скорости интерконверсии; k₁ - константа скорости образования ¹O₂* ; k₂ - константа окисления субстрата; k₃ - константа распада состояния ¹О₂* всеми остальными путями, кроме окисления субстрата; k₄ - константа возможного восстановления окисленного субстрата.

Тогда система кинетических уравнений для молярных концентраций соответствующих веществ запишется так:

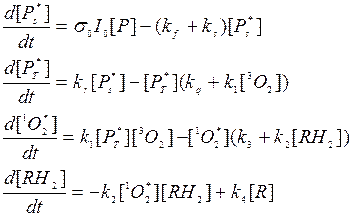(П1)

Z

Y

Х

a

b g

Рис. 10. Блок-схема взаимных превращений клеточных состояний при фотодинамическом поражении клеток.

Можно показать, что скорость протекания первых трех процессов велика по сравнению с последним. Предположим также, что k₁[³O₂] » k_q ,т.е. отсутствует «кислородное голодание». Тогда для концентрации синглетного кислорода можно записать:

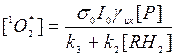(П2)

Здесь 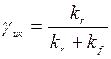- квантовый выход интерконверсии.

Подставляя (3) в последнее уравнение системы (2), а также вводя безразмерные переменные 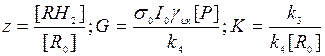, где за R₀ обозначена суммарная концентрация субстрата [R] + [RH₂], получим:

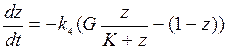(П3)

Уравнение (П3) описывает динамику окисления субстрата. Свяжем этот процесс с процессом гибели клеток, содержащих ФС. Будем считать, что скорость повреждения клеток пропорциональна доле окисленного субстрата, а скорость репараций – доле неокисленного субстрата. При этом существует постоянная вероятность необратимой гибели поврежденных клеток. Блок-схема взаимных превращений клеточных состояний показана на рис.10, где буквами a, b, g обозначены удельные скорости переходов клеток из соответствующих состояний. Система дифференциальных уравнений, соответствующих схеме рис.7, будет иметь вид:

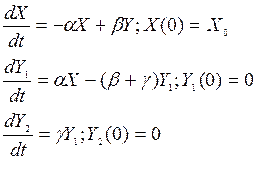(П4)

Уравнение (П3) вместе с системой (П4) образуют замкнутую модель поражения патологических клеток, в которой параметры G и K являются управляющими. Константа G пропорциональна исходной концентрации препарата и интенсивности излучения. Очевидно, G ¹ 0 только на время экспозиции (облучения) Т₀ , т.е. G = 0 при t > T₀ . Введем безразмерные переменные и параметры для системы (4)-(5), а также безразмерное время:

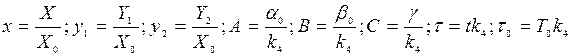(П5)

Окончательно модель ФДЭ описывается системой трех дифференциальных уравнений, если учесть, что 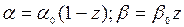(z – доля неокисленного субстрата). При этом условие Y₂ =0 в (П4) можно заменить условием сохранения полного числа клеток X + Y₁ +Y₂ = X₀

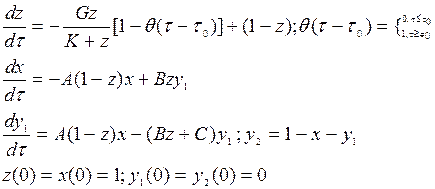(П6)

Решение системы (П6) может быть получено численно при задании параметров K,G,A,B,C. Константа k₄ важна для сравнения расчетных кривых с экспериментом и определяется эмпирическим путем (при наблюдении за облученными клетками через микроскоп). Справедливость описания ФДЭ системой уравнений типа (П6) неоднократно подтверждалась на опыте, так что она может рассматриваться как базовая при моделировании ФДЭ на ЭВМ.

Вернемся к системе уравнений (П1), в предположении о медленности процесса окисления субстрата по сравнению с предыдущими процессами сводящейся к одному уравнению:

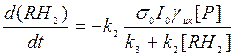, (П7)

получающемуся из (П3) при условии пренебрежения процессами репарации ( k₄ [R] « k₂ [RH₂]). Входящие сюда константы k₂ и k₃ естественносвязать со скоростями химического и физического тушения соответственно. Пренебрегая физическим тушением по сравнению с химическим, запишем:

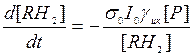(П8)

Поскольку 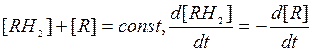, а если использовать введенную в (П3) безразмерную переменную 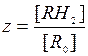, то получим, что 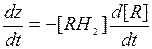. Гибель сенсибилизированных клеток мы связываем (в предположении об отсутствии репараций) с ростом доли окисленного субстрата [R]. Значит, уравнение (П8) удобно переписать для 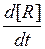, ввести безразмерную переменную y = 1-z и записать:

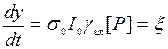, (П9)

где в правой части стоит величина, не зависящая от времени и концентрации субстрата, а определяемая только интенсивностью засветки и концентрацией введенного ФС (s₀ и g_ик – внутренние характеристики ФС). В предположении об отсутствии репаративных процессов система уравнений (П4) также сводится к одному уравнению:

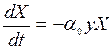, (П10)

где X означает численность выживших клеток. Уравнения (П9) и (П10) образуют систему 2-го порядка, имеющую решение:

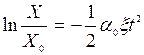(П11)

при условии y½_t=0 = 0 и прекращении засветки в момент t. Удобно ввести обозначение 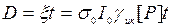- доза воздействия. Размерность величины D, при условии безразмерности [P], есть размерность энергии [Дж]. В соответствии с этим кривая (П11), изображенная в координатах 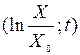, называется дозовой кривой. Она определяет относительную концентрацию выживших частиц X/X₀ в зависимости от времени облучения t и дозы облучения D. Коэффициент a₀ характеризует крутизну дозовой кривой (рис.9). В случае реализации ФДЭ с выполнением допущенных условий (пренебрежение репаративными процессами, преобладание химического механизма тушения, определение доли выживших клеток сразу после прекращения облучения) дозовая кривая, рассчитанная в соответствии с (П11), может сравниваться с экспериментом.

Литература.

1. А.Б. Рубин (ред.). Современные методы биофизических исследований: практикум по биофизике.- Высшая школа, М., 1988.

2. А.Б. Рубин (ред.). Молекулярные механизмы биологического действия оптического излучения.- Высшая школа, М., 1988.

3. С.А. Ахманов, Е.Б. Черняева (ред.). Фотодинамическое действие лазерного излучения на молекулы и клетки. – Изд. ВИНИТИ, сер. Итоги науки и техники, М., 1990.

4. М.В. Волькенштейн. Биофизика. – Наука, М., 1988.

5. Harris J.W. et al. The Red Cell Production, Metabolism, Destruction: Normal and Abnormal.- Harvard Univ. Press, Cambridge, 1970.

6. С.Д. Плетнев (ред.). Лазеры в клинической медицине.- Медицина, М., 1996.