Направленность химических процессов

В механических системах самопроизвольно протекают процессы, в которых уменьшается потенциальная энергия, т.е. критерием самопроизвольности служит неравенство ΔE_п<0. Для химических процессов имеются аналогичные критерии. В XIX веке таким критерием считали выполнимость условия ΔH<0 (принцип Бертло). Это казалось правдоподобным, т.к. при ΔH<0 (в экзотермической реакции) система переходит в состояние с меньшей энергией. Однако впоследствии было обнаружено много нарушений принципа Бертло (невозможность протекания некоторых экзотермических реакций и возможность – некоторых эндотермических). Поэтому принцип Бертло в настоящее время не применяется. Его нарушение связано с влиянием энтропии.

Состояние вещества можно охарактеризовать двояко: 1) Указать значения измеряемых свойств, например, температуру и давление. Это характеристики макросостояния. 2) Указать мгновенные характеристики каждой частицы вещества – ее положение в пространстве, скорость и направление перемещения. Это характеристики микросостояния.

Поскольку тела состоят из огромного количества частиц, то данному макросостоянию соответствует колоссальное число различных микросостояний. Это число называется термодинамической вероятностью W. С ней связано одно из фундаментальных свойств вещества – энтропия:

,

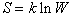где k – постоянная Больцмана.

Энтропию измеряют в Дж/К, а для одного моля – в Дж/(моль·К). По смыслу энтропия является мерой неупорядоченности системы. Так, для одного и того же вещества она имеет наибольшее значение в газообразном состоянии и наименьшее – в твердом, а для разных веществ в одном и том же агрегатном состоянии определяется сложностью структуры молекул. Любая система имеет тенденцию к самопроизвольному росту энтропии (ΔS>0). С другой стороны, согласно принципу Бертло, имеется тенденция к снижению энтальпии (ΔH<0). Эти два фактора учитываются в уравнении изобарно-изотермического потенциала:

G=H–TS ,

где T – абсолютная температура.

Величина G называется также энергией Гиббса и является одним из важнейших термодинамических потенциалов. При постоянных температуре и давленииизменение энергии Гиббса в процессе определяет возможность его самопроизвольного протекания:

ΔG=ΔH–TΔS

Если для некоторой реакции ΔG<0, то она может протекать самопроизвольно, при ΔG>0 реакция принципиально неосуществима; ΔG=0 отвечает состоянию равновесия.

График зависимости ΔG от температуры может иметь различный вид в зависимости от знаков ΔH и ΔS (рисунок 1.1).

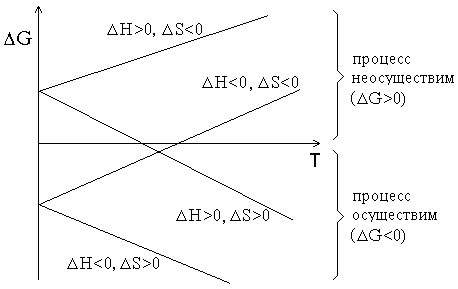
Рисунок 1.1 – Графики зависимостей ΔG от температуры.

Из рисунка 1.1 видно, что при ΔH<0 и ΔS>0 процесс протекает самопроизвольно при любых температурах. Напротив, при ΔH>0 и ΔS<0 процесс принципиально неосуществим. Если же знаки ΔH и ΔS совпадают, то реакция может протекать самопроизвольно в некотором интервале температур. ЕслиΔH=0 (реакция не сопровождается тепловым эффектом), то возможность протекания процесса полностью определяется энтропией. В случае, когда ΔS=0 определяющую роль играет энтальпийный фактор (соблюдается принцип Бертло).

Значение ΔS можно вычислить, пользуясь справочником, где приведены стандартные энтропии многих веществ (см. также таблицу 1 приложения).

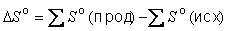
Знак ΔS можно легко определить, не пользуясь справочником, если неупорядоченность системы резко изменяется в ходе реакции:

CaCO₃(т) → CaO(т) + CO₂(г)

В продуктах реакции имеется газообразное вещество, а исходное вещество твердое, поэтому энтропия продуктов выше, чем исходных веществ. Следовательно, ΔS>0.

Существует также способ расчета ΔG° реакции через энергии Гиббса образования веществ 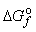, приводимые в справочниках (см. таблицу 1 приложения):

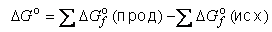
Полагается, что для простых веществ 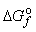= 0.

33. Тепловой эффект химической реакции или изменение энтальпии системы вследствие протекания химической реакции — отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру реагентов.

Чтобы тепловой эффект являлся величиной, зависящей только от характера протекающей химической реакции, необходимо соблюдение следующих условий:

§ Реакция должна протекать либо при постоянном объёме Q_v(изохорный процесс), либо при постоянном давлении Q_p(изобарный процесс).

§ В системе не совершается никакой работы, кроме возможной при P = const работы расширения.

Если реакцию проводят при стандартных условиях при Т = 298,15 К = 25 ˚С и Р = 1 атм = 101325 Па, тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔH_r^O. В термохимии стандартный тепловой эффект реакции рассчитывают с помощью стандартных энтальпий образования.

[Стандартная энтальпия образования (стандартная теплота образования)

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моль метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 76 кДж/моль.

Стандартная энтальпия образования обозначается ΔH_f^O. Здесь индекс f означает formation (образование), а перечеркнутый кружок, напоминающий диск Плимсоля^[1] — то, что величина относится к стандартному состоянию вещества. В литературе часто встречается другое обозначение стандартной энтальпии — ΔH_298,15⁰, где 0 указывает на равенство давления одной атмосфере^[2] (или, несколько более точно, на стандартные условия^[3]), а 298,15 — температура. Иногда индекс 0 используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[4]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе. «Диск Плимсоля» в таком случае означает собственно стандартное состояние вещества, независимо от его выбора.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298 K. Например, для йода в кристаллическом состоянии ΔH_I2(тв)⁰ = 0 кДж/моль, а для жидкого йода ΔH_I2(ж)⁰ = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH_{реакции}^O = ΣΔH_f^O (продукты) — ΣΔH_f^O (реагенты)

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеcя выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называютсяэкзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

]Температурная зависимость теплового эффекта (энтальпии) реакции

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

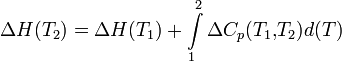
Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

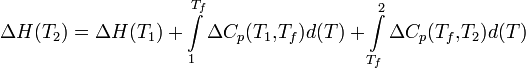
где ΔC_p(T₁,T_f) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода; ΔC_p(T_f,T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_f — температура фазового перехода.

]Стандартная энтальпия сгорания

Стандартная энтальпия сгорания — ΔH_гор^о, тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

]Стандартная энтальпия растворения

Стандартная энтальпия растворения — ΔH_раств^о, тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решетки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш > 0, а гидратация ионов — экзотермический, ΔH_гидр < 0. В зависимости от соотношения значений ΔH_реш и ΔH_гидр энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калиясопровождается выделением тепла:

ΔH_{раствKOH}^о = ΔH_реш^о + ΔH_гидрК^+о + ΔH_гидрOH^−о = −59 КДж/моль

Под энтальпией гидратации — ΔH_гидр, понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

]Стандартная энтальпия нейтрализации

Стандартная энтальпия нейтрализации — ΔH_нейтр^о энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔH_нейтр° = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔH_{гидратации}° ионов при разбавлении.

1-й закон — первое начало термодинамики. Представляет собой формулировку обобщённого закона сохранения энергии для термодинамических процессов. В наиболее простой форме его можно записать как 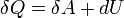, где 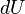есть полный дифференциал внутренней энергии системы, а 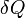и 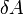есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что 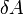и 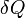нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось.

С аксиоматической точки зрения первое начало вводит в рассмотрение новую физическую величину — внутреннюю энергию, и описывает (постулирует) свойства этой переменной, основное из которых состоит в том, что она необходима для соблюдения закона сохранения энергии. Отсюда ясно, что корректно разбить изменение внутренней энергии в некотором процессе на теплоту и работу невозможно без носящих условный характер дополнительных соглашений (к ним, в частности, относится и так называемое «правило знаков»). Одно из таких соглашений состоит в том, что по формальным основаниям изменение внутренней энергии в химических реакциях (называемое в обиходе тепловым эффектом) мы вынуждены относить к работе (придуман даже специальный термин «химическая работа»; в неравновесной термодинамике по аналогичной формальной причине теплоту трения причисляют к работе). Смена правил разбивки изменения внутренней энергии на теплоту и работу приводит к изменению математического аппарата термодинамики. Примером может служить разгоревшийся во второй половине XX века спор о том, какая из двух логически безупречных версий СТО-релятивистской термодинамики — Планка или Отта — более правильна. После того, как Шмутцером был построен ещё один вариант (в котором, в отличие от работ и Планка, и Отта, температура выступала в качестве релятивистского инварианта), этот спор потерял смысл.

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия - это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

Если термомеханическую систему рассматривать как состоящую из макротела (газа) и поршня с грузом весом Р = p S, уравновешивающего давление газа р внутри сосуда, то такая система называется расширенной.

Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом E_пот =pSx = pV

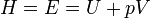
Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния

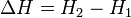
Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы. Если система каким-либо путём возвращается в исходное состояние (круговой процесс), то изменение любого её параметра, являющегося функцией состояния, равно нулю, отсюда 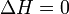, или же

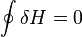
Дифференциал энтальпии, выраженный в собственных переменных — через энтропию S и давление p:

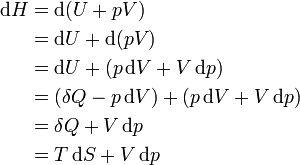
Поскольку в квазиравновесных процессах 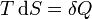— количество теплоты, подведенной к системе, отсюда вытекает физический смысл введения понятия энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении). Практическое применение этой функции основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении, когда резервуар открыт. Так,энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ.

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Мерой теплоты реакции служит изменение энтальпии ΔН, которая соответствует теплообмену при постоянном давлении. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная.

Энтальпией системы удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние системы, выбирают давление р и температуруТ

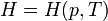
В этом случае изменение энтальпии в изобарическом процессе практически удобно рассчитывать, зная теплоемкость при постоянном давлении 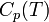(термохимический закон Кирхгофа):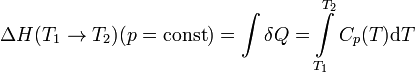

При этом используется эмпирическое разложение теплоёмкости в ряд по степеням Т:

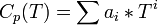
Энтальпия — величина аддитивная (экстенсивная), т. е. для сложной системы равна сумме энтальпий её независимых частей 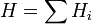. Подобно другим термодинамическим потенциалам, энтальпия определяется с точностью до постоянного слагаемого, которому в термодинамике часто придают произвольные значения (например, при расчете и построении тепловых диаграмм). При наличии немеханических сил величина энтальпии системы равна

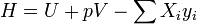
где 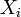— обобщённая сила; 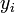— обобщённая координата.

34. соответствии с представлениями химической термодинамики каждое вещество заключает в себе определенную скрытую внутреннюю энергию U, кДж, которая является суммой кинетической и потенциальной энергии всех частиц, слагающих вещество и взаимодействующих между собой.
Внутренняя энергия зависит от природы вещества, его количества, физического состояния (агрегатного состояния и структуры); температуры и давления окружающей среды. Если количество вещества ограничить одним моль, температуру – 298 К (25^oС), давление – 1,01* 10⁵ Па (1 атм), то в этих условиях, называемыхстандартными, внутренняя энергия зависит только от природы и физического состояния вещества (его структуры и агрегатного состояния).
Абсолютное значение величины U измерить нельзя, так как далеко не всё известно о подробностях строения веществ, но проследить изменение внутренней энергии в процессе химических реакций и установить величину изменения ΔU, возможно.
Если системе из вещества или совокупности веществ сообщить извне энергию Q, то эта энергия будет расходоваться на изменение внутренней энергии системы ΔU и на совершение системой работы против внешних сил рΔV:

Q = ΔU + pΔV (1)

Эта зависимость является одной из форм закона сохранения энергии.

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия - это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

Если термомеханическую систему рассматривать как состоящую из макротела (газа) и поршня с грузом весом Р = p S, уравновешивающего давление газа р внутри сосуда, то такая система называется расширенной.

Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом E_пот =pSx = pV

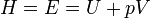
Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния

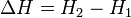
Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы. Если система каким-либо путём возвращается в исходное состояние (круговой процесс), то изменение любого её параметра, являющегося функцией состояния, равно нулю, отсюда 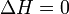, или же

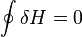
Дифференциал энтальпии, выраженный в собственных переменных — через энтропию S и давление p:

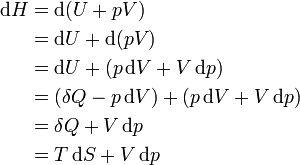
Поскольку в квазиравновесных процессах 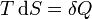— количество теплоты, подведенной к системе, отсюда вытекает физический смысл введения понятия энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении). Практическое применение этой функции основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении, когда резервуар открыт. Так,энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ.

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Мерой теплоты реакции служит изменение энтальпии ΔН, которая соответствует теплообмену при постоянном давлении. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная.

Энтальпией системы удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние системы, выбирают давление р и температуруТ

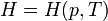
В этом случае изменение энтальпии в изобарическом процессе практически удобно рассчитывать, зная теплоемкость при постоянном давлении 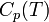(термохимический закон Кирхгофа):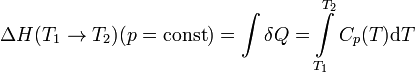

При этом используется эмпирическое разложение теплоёмкости в ряд по степеням Т:

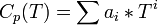
Энтальпия — величина аддитивная (экстенсивная), т. е. для сложной системы равна сумме энтальпий её независимых частей 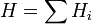. Подобно другим термодинамическим потенциалам, энтальпия определяется с точностью до постоянного слагаемого, которому в термодинамике часто придают произвольные значения (например, при расчете и построении тепловых диаграмм). При наличии немеханических сил величина энтальпии системы равна

где 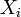— обобщённая сила; 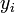— обобщённая координата.

Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многихэлементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количествоинформации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативностиисторического процесса).

Энтропия в информатике — степень неполноты, неопределённости знаний.

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

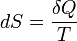где 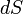— приращение энтропии; 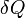— минимальная теплота, подведенная к системе; T — абсолютная температура процесса;

]Употребление в различных дисциплинах

§ Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.

§ Информационная энтропия — мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче.

§ Дифференциальная энтропия — энтропия для непрерывных распределений

§ Энтропия динамической системы — в теории динамических систем мера хаотичности в поведении траекторий системы.

§ Энтропия отражения — часть информации о дискретной системе, которая не воспроизводится при отражении системы через совокупность своих частей.

§ Энтропия в теории управления — мера неопределённости состояния или поведения системы в данных условиях.

Энтропия — функция состояния системы, равная в равновесном процессе количеству теплоты, сообщённой системе или отведённой от системы, отнесённому к термодинамической температуре системы.

Энтропия — функция, устанавливающая связь между макро- и микро- состояниями; единственная функция в физике, которая показывает направленность процессов. Энтропия — функция состояния системы, которая не зависит от перехода из одного состояния в другое, а зависит только от начального и конечного положения системы.

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:

Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж)

Определение

Классическим определением энергии Гиббса является выражение

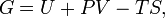
где 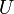— внутренняя энергия, 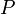— давление, 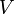— объем, 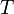— абсолютная температура, 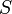— энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление p и температуру T:

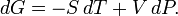
Для системы с переменным числом частиц этот дифференциал записывается так:

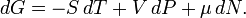
Здесь 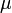— химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.