Распределение частиц по уровням энергии

Возможные значения энергии частиц системы рассматриваем как множество близко расположенных дискретных уровней, или состояний. Частицы идеального газа, находящиеся на одном уровне энергии, или в одном состоянии, отличаются проекциями импульса и положениями в пространстве. Найдем среднее число частиц в одном состоянии с энергией ε для газа с фиксированной температурой и концентрацией.

Для трехмерного газа среднее число частиц в единице объема с энергией в интервале описывается распределением Максвелла по энергии (2.48а)

.

Концентрацию n выражаем через химический потенциал, используя (2.62а):

,

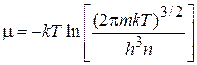тогда

,

Множитель выражаем через энергетическую плотность состояний в единице объема (П.2.5), или число уровней в единичном интервале энергии:

.

Распределение Максвелла получает вид

,

или

, (П.7.6)

где

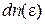– число частиц в интервале энергии ;

– число уровней в интервале .

Тогда среднее число частиц на уровне с энергией e, или заполненность уровня:

(П.7.7)

где – активность системы. Функция (П.7.7) называетсяраспределением Максвелла–Больцмана по состояниям.

Распределение по состояниям показано на рисунке. Ось энергии направлена вертикально, уровни энергии изображены горизонтальными линиями, частицы показаны кружочками. Из (П.7.7) следует:

1. Чем выше уровень энергии, тем меньше на нем частиц;

2. При низкой температуре заполнены лишь нижние уровни;

3. Среднее число частиц в состоянии равно активности

.

4. При повышении температуры частицы переходят между уровнями снизу вверх, заполняя верхние уровни и освобождая нижние;

5. Химический потенциал равен энергии уровня со степенью заполненности единица

.

Для классического газа уровень химического потенциала находится в нефизической области , показанной пунктиром на рисунке;

6. Площадь под кривой в интервале пропорциональна температуре

.

На рисунке учтено, что с ростом температуры химический потенциал и активность газа уменьшаются согласно (2.62а) и (2.62в).

Среднее число частиц в единичном интервале энергии около e

(П.7.8)

равно произведению числа состояний в единичном интервале энергии на число частиц в одном состоянии.

Для He при 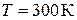, , 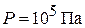со средней энергией молекулы

,

ранее получено

, .

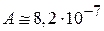Из (П.2.5)

с учетом при находим

,

,

.

Несмотря на малую степень заполненности уровней энергии , число частиц, приходящихся на интервал в один электрон-вольт около среднего значения энергии, достигает величины . Это связано с чрезвычайно большой плотностью состояний g, вызванной малостью постоянной Планка.

Термодинамический потенциал Гиббса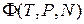

Система с переменным числом частиц описывается омега-потенциалом, не зависящим от числа частиц системы. Получим Ω-потенциал, используя термодинамический потенциал Гиббса.

Потенциал Гиббса определяется через свободную энергию

. (2.64)

Берем полный дифференциал (2.64), используем (2.61)

,

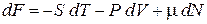находим

, (2.65)

тогда

.

При фиксированных P и T из (2.65) получаем

.

Интегрируем по N

. (2.66)

Здесь и далее число частиц является характеристикой макросостояния, поэтому . Термодинамический потенциал Гиббса равен химическому потенциалу, умноженному на среднее число частиц системы.

Из (2.64)

и (2.66) получаем

. (2.67)

W-потенциал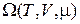

Определяем

, (2.68)

где учтено (2.67). Следовательно, омега-потенциал не зависит явно от числа частиц системы

.

Дифференцируем (2.68)

,

подставляем (2.61)

,

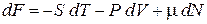получаем

,

откуда

,

,

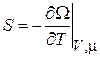. (2.69)

В результате уравнение состояния системы получает вид

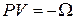. (2.69а)

Выразим Ω-потенциал через статистические характеристики системы с фиксированными температурой и объемом и с переменным числом частиц.