Статистическая обработка результатов анализа

Значениеизмеряемогоаналитическогосигнала –случайнаявеличина. Дляхарактеристикирезультатаанализаприменяютпонятияправильность, точность, воспроизводимость, чувствительность.

Мерой точности и воспроизводимости является величина случайной ошибки. Для некоторой концентрации С_i абсолютная случайная ошибка

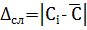; (1)

относительная случайная ошибка

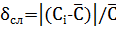, (2)

где 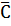– среднее арифметическое значение нескольких определений.

Мерой правильности является величина систематической ошибки. Для некоторой концентрации С_i абсолютная систематическая ошибка

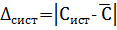(3)

относительная систематическая ошибка

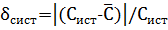, (4)

где С_ист – истинное значение определяемой концентрации.

Систематическиеошибки (например, смещение шкалы при настройке измерительногоприбора)устранимы. Случайныеошибкиполностьюустранить нельзя, можно только их уменьшить.

Случайные ошибки делают неточным результат анализа, а систематические – делают неверным сам анализ.

Чувствительность метода оценивают по крутизнезависимости в координатах "аналитическийсигнал –концентрацияопределяемоговещества".

Первую производную аналитического сигнала А по концентрации называют коэффициентом чувствительности k (или чувствительностью):

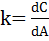(5)

Например, при фотометрическом определении Fe³⁺ используют его поглощающие свет комплексы с тиоцианат-ионами (SCN^–) или анионами сульфосалициловойкислоты (C₆H₃OHCOOHSO₃^–). Изрис. 1.1 следует:

dА₂/d(C) >dА₁/d(C).

Таким образом,второй метод чувствительнее первого.

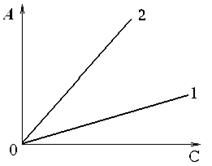
Рис. 1. Зависимость оптической плотности раствора от концентрации Fe³⁺ для тиоцианатных (1) и сульфосалицилатных (2) комплексов.

Обычно наблюдаемые в аналитической практике случайные значения подчиняется закону нормального распределения Гаусса (рис. 1.2):

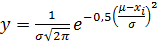, (6)

где y –плотностьвероятностираспределенияслучайнойвеличиных_i,μ –

математическоеожидание (среднееарифметическоезначениедлягенераль-

ной совокупности), σ – среднее квадратичное отклонение (расстояние от μ до

проекции точки перегиба на ось х).

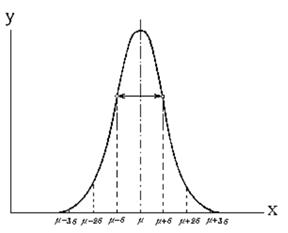
Рис.2. Кривая Гаусса

При проведении серии из n параллельных измерений в качестве результата выбирают среднее значение и приводят метрологические характеристикирезультатов анализа. Важнейшей из них является доверительныйинтервалε. Его рассчитывают по формуле:

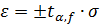(7)

гдеt_α,_f– значение критерия Стьюдента для доверительной вероятности α и

числа степеней свободы f; σ – среднее квадратичное отклонение.