Оценивание параметров и проверка статистических гипотез в случае выборок малого объема

Тема 7

Нормальный закон распределения

Случайная величина X называется распределенной по нормальному закону, если ее плотность f (х) имеет вид

.

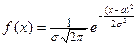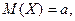
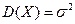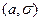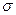Здесь . В этом случае пишут X ~ N , где – среднее квадратическое отклонение.

Решение типовых задач

Задача 1. При сортировке случайные значения веса зерна распределены нормально со средним значением 0,15 г и средним квадратическим отклонением 0,03 г. Нормальные всходы дают зерна, вес которых более 0,10 г. Определить: а) процент семян, от которых следует ожидать нормальные всходы; б) величину, которую не превзойдет вес отдельного зерна с вероятностью 0,99.

Решение. Обозначим Х – случайный вес зерна. По условию

,

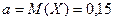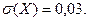
а) Процент семян, дающих нормальные всходы – это вероятность того, что взятое наугад зерно нормально взойдет. По условию нормальные всходы дают зерна, удовлетворяющие условию Х > 0,10.

Вероятность этого события найдем по формуле

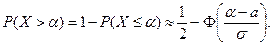
Подставляя числовые значения, получаем

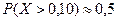
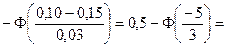
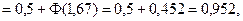
т. е. от 95,2% семян следует ожидать нормальных всходов.

б) Обозначим искомую величину веса через 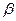. Воспользу­емся для ее нахождения формулой .

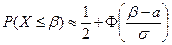Находим из условия 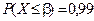или

; .

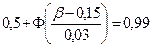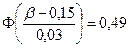По таблице значений функции 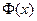находим 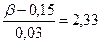, откуда 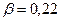. Таким образом, вес взятого наугад зерна не будет превышать 0,22 г с вероятностью 0,99.

Задача 2. Случайные отклонения диаметра детали, выпускаемой цехом, от номинала распределены нормально. Математическое ожидание диаметра детали равно 20 мм, а дисперсия 0,36 мм. Найти:

1) вероятность того, что диаметр наудачу взятой детали: а) имеет размеры от 19 до 22 мм; б) отличается от математического значения не более чем на 1 мм (по абсолютной величине);

2) границы, в которых следует ожидать величину диаметра детали, чтобы вероятность невыхода за эти границы была равна 0,9876.

Решение. Обозначим Х – величина диаметра детали. По условию 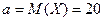, , 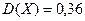тогда .

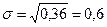1.а) Найдем вероятность 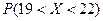, для чего воспользуемся формулой

.

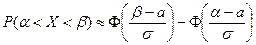Получаем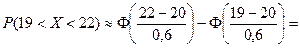

.

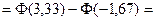
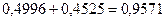1.б) Найдем вероятность 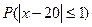. Имеем

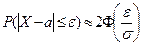или .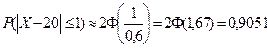

2) По условию 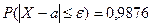. По таблице значений 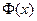находим 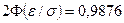значит, 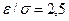, отсюда .

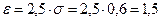Диаметр детали X удовлетворяет неравенству 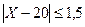. Отсюда находим 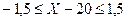или 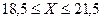, т.е. 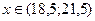с вероятностью 0,9876.

Задача 3. Результат взвешивания химреактива распределен по нормальному закону со средним квадратическим отклонением веса 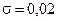г. Какое отклонение массы реактива можно гарантировать с вероятностью 0,2?

Решение. В условии задачи дано, что 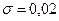, , 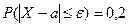где 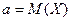. Нужно найти .

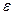Воспользуемся формулой .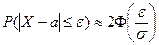

Согласно условию задачи 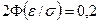. По таблице значений функции Лапласа 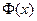имеем .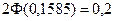

Значит, 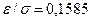, откуда 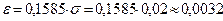. Итак, с вероятностью 0,2 можно ожидать отклонения массы реактива, равного 0,0032 г.

Задачи для отчета преподавателю

Блок А

А 7.1.Автомат штампует детали. Контролируется длина детали, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Среднее квадратическое отклонение равно 3,6 мм. Найти вероятность того, что: а) длина наудачу взятой детали заключена в границах от 40 до 55 мм; б) отклонение длины изготовленной детали проектной по абсолютной величине не превзойдет 5 мм.

А 7.2.Производится измерение расстояния между 2 пунктами. Случайные ошибки подчинены нормальному закону. Найти вероятность того, что измерение расстояния будет произведено с ошибкой не более 60 мм, если 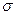= 50 мм.

А 7.3.Автомат изготовляет шарики для подшипников. Шарик считается годным, если отклонение его диаметра от проектного не превосходит 0,6 мм. Считая, что диаметр изготовленного шарика есть нормально распределенная величина, среднее квадратическое отклонение которой равно 0,3 мм, найти, сколько годных шариков будет среди 100 изготовленных.

А 7.4.Диаметр валика – случайная нормально распределенная величина, среднее квадратическое отклонение которой равно 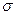= = 5 мм. Найти длину интервала, симметричного относительно
математического ожидания, в который с вероятностью 0,9545 попадет длина диаметра валика.

А 7.5.Ведется стрельба по цели из орудия. Средняя дальность полета снаряда – 1000 м. Найти долю выпускаемых снарядов, дающих перелет до 60 м, если среднее квадратическое отклонение дальности полета снаряда равно 30 м.

А 7.6.Известно, что вес клубня картофеля подчиняется нормальному закону с математическим ожиданием 125 г и 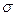= 15 г. Найти вероятность того, что вес наудачу взятого плода будет: а) не менее 200 г; б) не более 300 г.

А 7.7.Ошибка измерительного прибора – случайная величина, распределенная по нормальному закону. Ее среднее квадрати­ческое отклонение 4 мм. Найти вероятность того, что в 6 независи­мых измерениях ошибка (по модулю): а) превзойдет 3 мм менее 4 раз; б) хотя бы 1 раз окажется в интервале от 0,6 до 2,0 мм.

А 7.8.Деталь, изготовленная автоматом, считается годной, если отклонение контролируемого размера от номинала не превышает 10 мм. Точность изготовления детали характеризуется 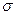= 5 мм. Считая, что отклонение размера детали от номинала есть нормально распределенная случайная величина, найти долю годных деталей, изготовляемых автоматом. Какой должна быть точность изготовления, чтобы процент годных деталей повысился до 98%?

А 7.9.Измеряемая величина Х подчиняется закону N (10; 5). Найти симметричный относительно математического ожидания интервал, в который с вероятностью p попадет измеренное значение. Провести расчеты для: а) p = 0,9973; б) p = 0,9545; в) p = 0,6827.

А 7.10.Случайная величина Х распределена по нормальному закону N (25; 0,45). В какой интервал попадут ее значения с вероятностью 0,9545?

А 7.11.Деталь изготавливается на станке. Ее размер Х представляет собой случайную величину, распределенную по нормальному закону со средним значением 20 см и дисперсией 0,2 см². Какую относительную точность изделия можно гарантировать с вероятностью 0,95?

А 7.12.В нормально распределенной совокупности 15% значений Х меньше 12 и 40% значений Х больше 16,2. Найти среднее значение и дисперсию этого распределения.

А 7.13.Коробки с шоколадом упаковываются автоматически. Их средняя масса равна 1,06 кг. Известно, что 5% коробок имеют массу, меньшую 1 кг. В предположении нормальности определить, каков процент коробок, масса которых превышает 940 г.

А 7.14.Химический завод изготовляет серную кислоту плотности 1,84 г/см³. В результате статистических испытаний обнаружено, что практически 99,9% всех выпускаемых реактивов имеют плотность в интервале (1,82; 1,86). Предполагается, что плотность серной кислоты имеет нормальное распределение. Найти вероятность того, что кислота удовлетворяет стандарту, если для этого достаточно, чтобы ее плотность не отклонялась от номинала более чем на 0,01 г/см³.

А 7.15.Случайная величина X распределена по нормальному закону N (1; 0,3). Найти вероятности следующих событи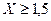й: и .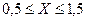

А 7.16.Ошибка высотомера распределена нормально с параметрами 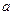= 20 мм, 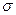= 10 мм. Найти вероятность того, что отклонение ошибки от ее среднего значения не превзойдет 5 мм по абсолютной величине.

А 7.17.Случайная величина Х подчиняется закону N (1; 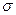). Известно, что Р(X < 2) = 0,99. Вычислить М(Х ²) и Р(Х ² >2).

А 7.18.Случайная величина Х распределена по закону N ( 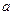, 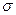). Найти вероятность того, что отклонение величины Х от ее математического ожидания не превзойдет величины 2 .

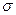А 7.19.В нормально распределенной совокупности 15% значений Х меньше 15 и 40% значений Х больше 18,2. Найт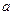и и 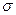этого распределения.

А 7.20.Диаметр электродвигателя есть нормально распределен­ная случайная величина с параметрами 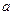= 100 мм и 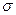=1,6 мм. Найти вероятность того, что диаметр случайно взятого электродвигателя находится в интервале (98; 101).

А 7.21.При измерении расстояний до удаленных предметов ошибка подчинена нормальному закону с 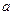= 20 м и 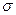= 10 м. Определить вероятность того, что измеренное расстояние отклоняется от действительного в ту или иную сторону не более чем на 15 м.

А 7.22.Средний размер детали 8 см, а дисперсия равна 0,0004 см². В предположении о нормальном распределении определить максимальное отклонение размера диаметра наудачу взятой детали от среднего размера, которое можно гарантировать
с вероятностью не менее чем 0,9973.

А 7.23.Изделия, выпускаемые цехом, по своим линейным размерам распределяются по нормальному закону с математи­ческим ожиданием, равным 6 см. Известна вероятность, равная 0,9758, что наудачу взятое изделие будет иметь размеры в границах от 5,95 до 6,05 см.
Найти дисперсию этой случайной величины.

А 7.24.Длина изготовляемой детали есть случайная величина, распределенная по нормальному закону с 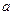= 10 см и 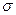= 0,2 см. Найти вероятность брака, если допустимые размеры детали должны быть 10 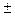0,3 см. Какую точность длины изготовленной детали
можно гарантировать с вероятностью 0,9758?

А 7.25.На автомате изготавливают заклепки. Диаметр их головок представляет собой случайную величину X, распределенную по нормальному закону с параметрами 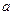= 2 мм и 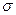² = 0,01 мм². Найти вероятность брака, если допустимые размеры головок 2 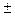0,05 мм. Какие размеры диаметра головок заклепки можно
гарантировать с вероятностью 0,9545?

Тема 8

Оценивание параметров и проверка статистических гипотез в случае выборок малого объема

Решение типового примера

С целью сравнения качественных и количественных показателей двух однотипных производственных процессов A и B проведены выборки (x₁, x₂, …, x_n) и (y₁, y₂, …, y_n) объемов
n_x и n_y соответственно.

1. Для каждой выборки оценить математическое ожидание a и дисперсию 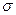² путем: а) вычисления выборочных средних 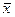и 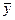, исправленных выборочных дисперси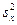й и 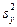; б) построения доверительных интервалов для математических ожиданий a_x и a_у и дисперси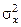й и 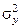с надежностью γ = 0,95.

2. Допуская, что выборки (x₁, x₂, … , x_n) и (y₁, y₂, … , y_n) осуществлены из нормально распределенных генеральных совокупностей X и Y с параметрами (a_x, σ_x) и (a_y, σ_y) соответственно, при уровне значимости α = 0,05: а) пользуясь критерием Фишера, проверить гипотезу 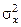= 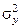и установить, является ли один из производственных процессов эффективнее другого; б) пользуясь критерием Стьюдента, проверить гипотезу a_x = a_у и установить, можно ли считать распределение между средним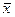и и 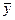случайным, или оно является существенным и связано с различием производственных процессов.

В таблице приведены показатели производительности труда рабочего, изготавливающего на станке детали до (режим работы A) и после (режим работы B) усовершенствования обработки деталей.

Режим работы	Количество деталей за смену
А
В

Проведем количественное и качественное сравнение производительности труда рабочего для режимов работы А и В.