Сложность структуры атома. Ядерная модель Э. Резерфорда
В основе атомно-молекулярной теории строения вещества лежит представление о возможности разделения физического тела на малые части, каждая из которых сохраняет химические свойства тела. Эти части были названы молекулами.
Предполагалось, что молекулы сложного состава можно разделить на части, называемые атомами. Атомы в химических реакциях не изменяются. Если допустить существование движущихся атомов и молекул, то можно объяснить многие наблюдаемые на опыте свойства физических тел. При этом считалось, что опытные факты можно истолковать, считая атомы и молекулы точечными телами. Однако в конце XIX – начале XX в. были открыты явления, заставляющие сделать предположение о сложности строения атомов и молекул.
Изучение прохождения электрического тока через газы и растворы позволило обнаружить одну из составных частей атома и молекулы – электрон.
При изучении прохождения электрического тока через растворы электролита были открыты законы электролиза и введено представление о существовании положительного и отрицательного заряженных атомов или групп атомов – катионов и анионов.
Эти факты привели к мысли о том, что атом можно представить как сложное образование, состоящее из электронов и области, несущей положительный заряд. Возник вопрос об относительном расположении электронов и положительно заряженной остальной части атома.
В 1904 году В. Томсон и Д. Д. Томсон предложили модель строения атома. Атом представляет положительно заряженный шар, в котором вкраплены отрицательно заряженные электроны.
В том же году японский физик Х. Нагаока предложил иную модель строения атома: атом имеет строение, напоминающее строение планеты Сатурн с её кольцами спутников. Основная часть атома - положительно заряженный шар, вокруг которого по кольцевым орбитам вращаются электроны.
В 1906 – 1911 гг. в лаборатории Э. Резерфорда было изучено прохождение через фольгу дважды ионизированных атомов гелия – α-частиц. Оказалось, что область положительного заряда атома очень невелика по размерам, что противоречило модели В. Томсона и Д. Д. Томсона. Э. Резерфорд использовал планетарную модель Х. Нагаоки. Однако он предложил в отличие от Нагаоки, что масса атома почти целиком сосредоточена в области положительного заряда. Эта область была названа ядром атома. Ядерная модель атома предложена Э. Резерфордом в 1911 г. Но она не могла объяснить факта устойчивости атома: ведь согласно законам электродинамики электроны должны были бы излучать электромагнитные волны, теряя кинетическую энергию и уменьшая свою скорость, пока не упадут на ядро.
В дальнейшем изучение строения атома развивалось по двум направлениям – исследование атомного ядра и электронной оболочки атома. Первая количественная теория простейшего атома водорода была разработана Н. Бором в 1913г.
В 1913 г. Н. Бор предложил модель атома водорода, исходя из гипотезы Резерфорда, дополненной новыми положениями:
1. Электрон может вращаться по определённым круговым орбитам, не излучая энергии.
2. Ближайшая к ядру орбита отвечает нормальному, наиболее устойчивому состоянию атома.
3. Поглощение и излучение атомом энергии происходят лишь при перескоке электрона с одной орбиты на другую.
Начала волновой механики.
Открытия физики конца XIX - начала XX в. привели к выводу о том, что свет, который раньше рассматривался как пример волнового процесса, можно рассматривать как совокупность частиц (фотонов), обладающих механическими характеристиками движения – массой, энергией и импульсом. В 1900 г. М. Планком было предположено, что процесс излучения атомами световой энергии происходит не непрерывно, а порциями, квантами, величина которых зависит от частоты испускаемого света:
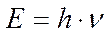
В 1905 г. А. Эйнштейн показал, что масса тела связана с его энергией соотношением 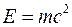 . Уравнения Планка и Эйнштейна дают возможность получить соотношение между массой фотона и длиной волны света, или частотой световых колебаний:
. Уравнения Планка и Эйнштейна дают возможность получить соотношение между массой фотона и длиной волны света, или частотой световых колебаний:
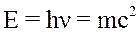
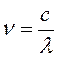
В 1924 г. Луи де Бройль предположил, корпускулярно волновая природа присуща не только свету, но и любым другим микрочастицам. При этом длина волны, соответствующая данной частице:
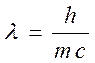
В 1927 г. Девиссон и Джермер обнаружили, что при дифракции электронов на никеле возникает дифракционная картина, сходная с дифракцией света на кристаллической решетке. Это явление получило название дифракции электронов. Оно считается экспериментальным доказательством существования волн де Бройля или корпускулярно-волнового дуализма электронов.
В волновых свойствах электрона заложен один из принципов волновой механики.
Вторым является принцип неопределённости Гейзенберга (1925г.).
В механике наблюдение волнового процесса – периодического колебания сплошной среды – позволяет определить длину волны и скорость её распространения. Чем больше область пространства, в котором распространяется волна, тем точнее можно определить эти характеристики. Иначе обстоит дело при переходе к объектам микромира. Гейзенберг показал, что точное определение положения электрона на орбите и его скорость не могут быть зафиксированы. Произведение неопределённостей положения (Δx) и скорости (Δp) никогда не может быть меньше, чем h/me:
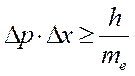
или
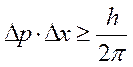
Промежуток пространства, в котором вероятность нахождения электрона велика, называется электронным облаком.
А часть околоядерного пространства, которая охватывает около 90% электронного облака, называется атомной орбиталью.
Представление об атоме с определёнными орбитами заменяется в волновой механике представлением о вероятном нахождении электрона в той или иной части атома. Оценка этой вероятности производится при решении уравнения Шредингера, описывающего движение электрона.
Исходя из представления о наличии у электрона волновых свойств Шредингер в 1925 г. предположил, что состояние движущегося в атоме электрона должно описываться известным в физике уравнением стоячей электромагнитной волны. Подставив в это уравнение выражение де Бройля (λ=h/mv), он получил новое уравнение, связывающее энергию электрона с пространственными координатами и так называемой волновой функцией (ψ), соответствующей в этом уравнении амплитуде трёхмерного волнового процесса.
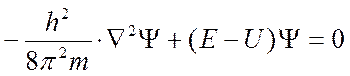
Е – полная энергия, U – потенциальная энергия электрона, Ñ2Y – вторая производная волновой функции по осям х, у, z 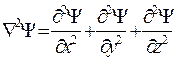
Особенно важное значение для характеристики состояния электрона имеет волновая функция ψ. Подобно амплитуде любого волнового процесса, она может принимать как положительные, так и отрицательные значения. Однако величина ψ2 всегда положительна. Причем чем больше значение ψ2 в данной области пространства, тем выше вероятность того, что электрон проявит здесь своё действие, т.е. его существование будет обнаружено в каком-либо физическом процессе.
Более точным будет следующее утверждение: вероятность обнаружения электрона в некотором малом объеме ΔV выражается произведениемψ2ΔV. Таким образом, сама величина ψ2 выражает плотность вероятности нахождения электрона в соответствующей области пространства.
Квантовые числа
Для электрона, находящегося под действием сил притяжения к ядру, уравнение Шредингера имеет решения не при любых, а только при определённых значениях энергии. Решением этого уравнения являются 3 квантовых числа (n, l, m).
Энергия электрона в реальном атоме квантована.
Возможные энергетические состояния электрона в атоме определяются величиной главного квантового числа n, которое может принимать положительные целочисленные значения: 1, 2, 3, … и т.д. Наименьшей энергией электрон обладает при n = 1; с увеличением n энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определённым значением главного квантового числа, принято называть энергетическим уровнем электрона в атоме: при n = 1 электрон находится на первом энергетическом уровне, при n = 2 на втором и т.д.
Главное квантовое число определяет и размеры электронного облака. Для энергетических уровней электрона в атоме (т.е. для электронных слоёв или оболочек), соответствующих различным значениям n, были приняты следующие буквенные обозначения:
Главное квантовое число n 1 2 3 4 5 6 7
Обозначение энергетического уровня K L M N O P Q
Не только энергия электрона в атоме не может быть произвольной. Произвольной не может быть и форма электронного облака. Она определяется орбитальным (побочное) квантовым числом l,которое можетпринимать значенияот 0 до (n – 1),где n – главное квантовое число. Различным значениям n отвечает разное число возможных значений l. Так, при n = 1 возможно только одно значение орбитального квантового числа l = 0, при n = 2 l может быть равно 0, 1, при n = 3 возможны значения l = 0, 1, 2.
Состояния электрона, характеризующиеся различными значениями l, принято называть энергетическими подуровнями электрона в атоме. Этим подуровням присвоены следующие буквенные обозначения:
Орбитальное квантовое число l 0 1 2 3
Обозначение энергетического подуровня s p d f
Из уравнения Шредингера также следует, что и ориентация электронного облака в пространстве не может быть произвольной: она определяется значением третьего, так называемого магнитного (азимутального) квантового числа m.
Магнитное квантовое число может принимать любые целочисленные значения, как положительные, так и отрицательные, в пределах от +l до –l через нуль. Так, для s-подуровня (l = 0) возможно только одно значение m = 0; для р-электронов (l = 1) возможны m = 1, 0,–1; при l = 2 (d-подуровень) возможны пять различных значений m = 2, 1, 0,–1,–2.
Состояние электрона в атоме, характеризующееся определёнными значениями квантовых чисел n, l, m, т.е. определёнными размерами, формой и ориентацией в пространстве электронного облака, получило название атомной электронной орбиталью.
Электронные подоболочки обозначают по типам соответствующих им линий в атомных спектрах:
s-подоболочка названа по «резкой» s-линии – sharp;
p-подоболочка названа по «главной» p-линии – principal;
d-подоболочка названа по «диффузной» d-линии – diffuse;
f-подоболочка названа по «фундаментальной» f-линии – fundamental.
Исследования атомных спектров привели к выводу, что, помимо квантовых чисел n, l, m, электрон характеризуется ещё одной квантовой величиной, не связанной с движением электрона вокруг ядра, а определяющей его собственное состояние. Эта величина получила название спинового квантового числа или просто спина: спин обозначают буквой s. Спин электрона может иметь только два значения: +½ и – ½.
Четыре квантовых числа – n, l, m, s – полностью определяют состояние электрона в атоме.
