Гальванический элемент Даниэля-Якоби

Гальванический элемент Даниэля-Якоби (рис. 7.1), который состоит из медной и цинковой пластинок, опущенных в растворы своих солей. На поверхности цинковой пластинки устанавливается равновесие

Zn 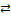Zn²⁺ + 2ē,

которому соответствует потенциал j_Zn. На поверхности медной пластинки устанавливается равновесие

Cu 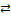Cu²⁺ + 2ē,

которому соответствует равновесный потенциал j_Сu.

Потенциал цинкового электрода имеет более отрицательное значение, поэтому при замыкании внешней цепи электроны будут переходить от цинка (анод) к меди (катод). В результате этого процесса равновесие на аноде (Zn) сместится вправо и в раствор перейдет дополнительное количество ионов цинка (происходит растворение анода). В то же время равновесие на медном электроде сместится влево и произойдет выделение меди на катоде.На аноде образуется избыток электронов, поэтому анод в гальванических элементах заряжен отрицательно, а катод – положительно.

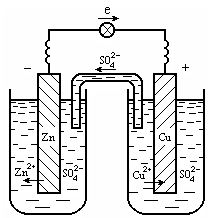
Рис. 7.1. Медно-цинковый гальванический элемент

Т.о. при замыкании внешней цепи возникают самопроизвольные процессы растворения цинка на цинковом электроде и выделения меди на медном электроде.Электроны от анода по внешней цели протекают к катоду.Электрическую цепь замыкает движение ионов в растворах.

Схема гальванического элемента, заменяющая рисунок, записывается следующим образом:

Zn½Zn²⁺║Cu²⁺½Cu .

(А): Zn- 2ē = Zn²⁺,(окисление)

(К): Cu²⁺ + 2ē = Cu⁰,(восстановление)

Zn + Cu²⁺ = Zn²⁺ + Cu .

Суммарная реакция, протекающая в гальваническом элементе, называется токообразующей.

Причиной возникновения и протекания электрического тока в гальваническом элементе является разность электродных потенциалов (ЭДС) двух окислительно-восстановительных систем, соединенных между собой. ЭДС (ξ) любого гальванического элемента определяется общей формулой:

или

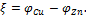
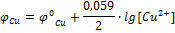
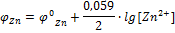
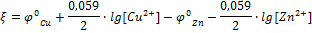
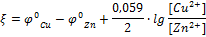
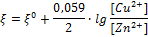
Так как ξ может иметь только положительное значение, то 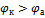, т.е. катодом является электрод с более высоким электродным потенциалом.

При таком осуществлении окислительно-восстановительной реакции ее энергия превращается в электрическую энергию, которую можно использовать, включив во внешнюю цель устройство, потребляющее электрическую энергию (например, электронагревательный прибор, электрическую лампу и т.п.).

С течением времени разность потенциалов будет снижаться, т.к. концентрация ионов цинка, а следовательно, и потенциал цинкового электрода будут увеличиваться, а концентрация ионов меди и потенциал медного электрода постепенно будут снижаться. Данные процессы будут продолжаться до тех пор, пока не выровняются потенциалы электродов ( 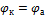) или не растворится весь цинк (высадится вся медь), т.е. пока ЭДС не станет равной нулю.

Как уже было показано, электроды, а следовательно, и гальванические элементы могут быть созданы не только для реакции окисления-восстановления металлов, но и для любых веществ и окислительно-восстановительных реакций, происходящих в растворах или расплавах. Например, для реакции в растворе

2KMnO₄ + 5Na₂SO₃ + 3H₂SO₄ = 2MnSO₄ + 5Na₂SO₄ + K₂SO₄ + 3H₂O

процессы окисления и восстановления можно разделить в виде полуреакций :

на аноде: 5 ½SO₃^2- + H₂0 = SO₄^2- + 2H⁺ + 2ē; (0,17 В),

на катоде: 2 ½ MnO₄^- + 8H⁺ + 5e = Mn²⁺ + 4H₂O (1,51 В).

2MnO₄^- + 5SO₃^2- + 6H⁺ + 10ē = 2Mn²⁺ + 5SO₄^2- + 3H₂O + 10ē.

Токообразующая реакция:

2MnO₄^- + 5SO₃^2- + 6H⁺ = 2Mn²⁺ + 5SO₄^2- + 3H₂O.

Для осуществления таких реакций обычно используют катализатор, который одновременно является проводником электронов, например платину (рис. 7.2).

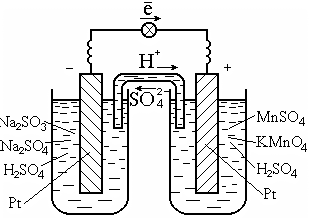
Рис. 7.2. Гальванический элемент на окислительно-восстановительной реакции в растворе

Схема гальванического элемента:

Pt | SO₃^2-, SO₄^2-, H⁺|| MnO₄^-, Mn²⁺, H⁺| Pt .

Значения стандартных электродных потенциалов полуреакций приводятся в справочниках. ЭДС такого элемента при стандартных условиях можно определить как разность потенциалов для полуреакций восстановления (окислителя) и окисления (восстановителя).

ξ = Dj⁰ = j⁰ (MnО₄^-/ Mn²⁺) -j⁰ (SO₄^2- / SO₃^2-) = 1,51 - 0,17 = 1,34 B.

Если при этом ЭДС положительна, то реакция возможна при стандартных условиях, так как DG реакции и электрическая работа (ЭДС) связаны между собой соотношением:

DG = -n·F·ξ.

Таким образом, разность потенциалов на электродах можно не только непосредственно измерить, но и вычислить из чисто химических экспериментальных данных. В случае нестандартных условий потенциал электрода и ЭДС элемента рассчитывается по формуле Нернста.