Большое каноническое распределение

Рассматривается идеальный газ с 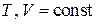, обменивающийся энергией и частицами с термостатом. Распределение дает вероятность того, что система имеет N частиц и находится в элементе объема 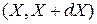фазового пространства.

Распределение микросостояний по фазовому пространству

При 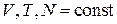система описывается каноническим распределением (2.16)

.

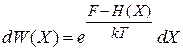Свободная энергия F зависит от числа частиц. Выражаем ее через W-потенциал, не зависящий от N, используя (2.68)

.

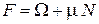Получаем большое каноническое распределение –вероятность для системы иметь N частиц и находиться в элементе объема 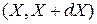фазового пространства

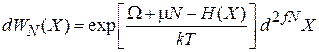. (2.70)

Интеграл состояния

В условие нормировки

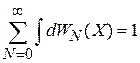
подставляем (2.70)

.

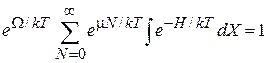Определяем интеграл состояния большого распределения

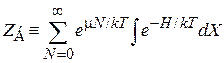. (2.71)

Условие нормировки дает

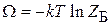.(2.72)

Используем статистический интеграл канонического распределения (2.17)

.

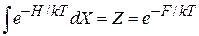Из (2.71) получаем связь между Z и Z_Б

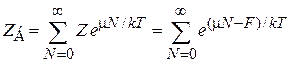. (2.73)

Для газа из N одинаковых частиц

,

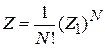тогда

,

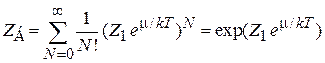где использовано разложение экспоненты в степенной ряд

.

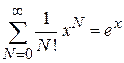Учитывая активность (2.62б)

,

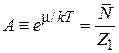получаем

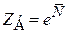. (2.74)

Статистический интеграл большого канонического распределения равен экспоненте от среднего числа частиц системы.

Из (2.69а), (2.72), и (2.74) получаем омега-потенциал и уравнение состояния

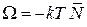, (2.74а)

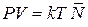. (2.74б)

Уравнение (2.74б) является обобщением уравнения Менделеева–Клапейрона на идеальный газ с переменным числом частиц.

Большое каноническое распределение

Используем (2.70) и (2.72)

,

,

,

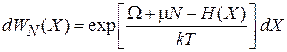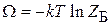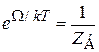получаем

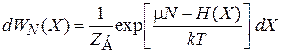. (2.75)

Вероятность появления N частиц в системе

Интегрируем (2.75) по фазовому пространству и находим вероятность N частиц в системе

.

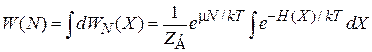С учетом (2.17)

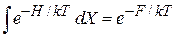
вероятность появления N частиц в системе

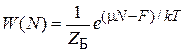. (2.76)

Согласно (2.73)

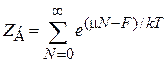
вероятность (2.76) удовлетворяет условию нормировки

.

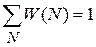Термодинамические характеристики системы

Из определения омега-потенциала получены соотношения (2.69)

,

,

.

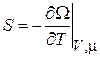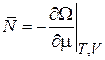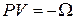Подставляем (2.72) и (2.74)

,

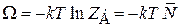находим

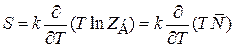, (2.77)

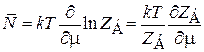. (2.78)

Физический смысл (2.78)

С учетом (2.73) и (2.76)

,

,

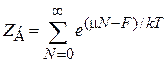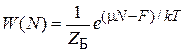выражение (2.78) сводится к определению среднего числа частиц

.

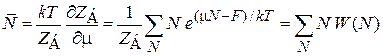ПРИМЕРЫ

Вывод формулы Больцмана

Получим формулу Больцмана (2.76)

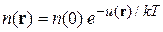
из условия термодинамического равновесия.

Используем химический потенциал (2.62а) идеального газа атомов, совершающих поступательные движения:

,

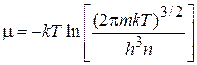и электрохимический потенциал (2.59)

,

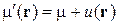где 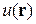– потенциальная энергия частицы в точке 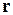, тогда

.

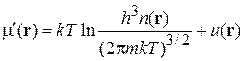При 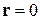полагаем 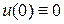и получаем электрохимический потенциал в начале координат

.

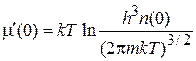При термодинамическом равновесии химический потенциал одинаков во всех точках системы согласно (2.60)

,

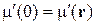тогда

,

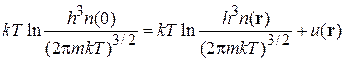получаем

.

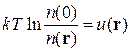Откуда следует формула Больцмана

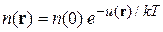. (П.7.12)