Нормування класів точності засобів вимірювання

Приклад №12

Вольтметр має шкалу, яка відградуйована в діапазоні 0 ...30 В; позначення класу точності на шкалі: 2,5. Обчислити абсолютну похибку вольтметра.

Дано:

k =2,5

N = 30 В

_____________________

Δ_х - ?

Розв’язок

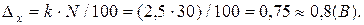
Відповідь:Δ_х = 0,8 В.

Приклад №13

Позначення класу точності k на шкалі омметра 1,5; шкалу відградуйовано в діапазоні 0 ... ∞кОм; довжина шкали L= 100мм; відстань між поділками шкали біля значення вимірюваного опору l_x= 5 мм; різниця відліків за цими поділками R_x = 0,005 кОм. Обчислити похибку результату вимірювання.

Дано:

k =1,5

L = 100 мм

l_x = 5 мм

R_x = 0,005 кОм

Δ_R - ?

Розв’язок

Чутливість омметра у точці відліку

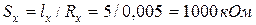
Абсолютна похибка вимірювання

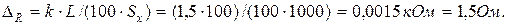
Відповідь:Δ_R = 1,5 Ом.

Приклад №14

Лічильник електричної енергії має клас точності 1,0. Обчислити похибку, яку він може допустити при відліку 100 кВт^.год.

k =1,0

N = 100 кВт·год.

___________

Δ_х - ?

Розв’язок

У засобах вимірювання із мультиплікативною похибкою визначають абсолютну похибку вимірювання за формулою: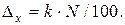

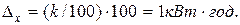
Відповідь:Δ_х = ±1 кВт·год.

Приклад №15

Цифровий вольтметр класу точності 0,02/0,01 з верхнім діапазоном вимірювання U_k=99,99 В вимірює напругу U_V = 75 В. Обчислити абсолютну похибку вимірювання.

Дано:

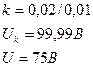
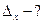
Розв’язок

Межа допустимої відносної похибки 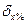визначається за формулою:

.

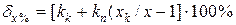Тут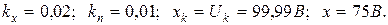

Тоді

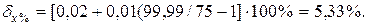
Абсолютна похибка вимірювання обчислюється за формулою:

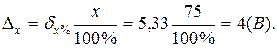
Відповідь:Δ_х = ±4 В.

Обробка результатів прямих вимірювань.

Приклад №16

Проведено ряд вимірювань за допомогою вольтметра магнітоелектричної системи. При цьому одержано такі результати: 122, 118, 120, 121, 119,120 (В). Визначити середнє значення виміряної напруги, його СКВ. Представити результат, вказавши границі надійного інтервалу, в який потрапляє результат вимірювання із заданою ймовірністю Р = 0,95 (коефіцієнт Стьюдента дорівнює 2,571).

Дано:

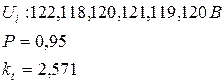
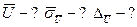
Розв’язок

1. Знайдемо математичне сподівання для ряду вимірювань

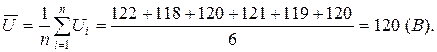
2. Визначимо випадкові відхилення

,

,

,

,

,

.

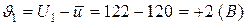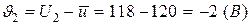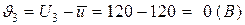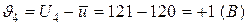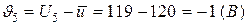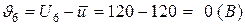3. Перевіримо, чи сума випадкових відхилень дорівнює нулю

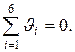
4. Знайдемо оцінку експериментального середнього квадратичного відхилення

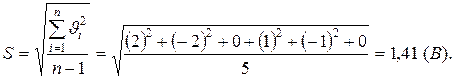
5. Визначимо середнє квадратичне відхилення середнього арифметичного

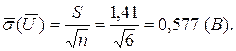
6. Знайдемо надійні границі результату вимірювання

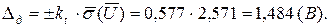
7. Представимо результат у відповідності до стандартної форми :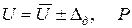

U= (120,000 B ± 1,484) B, P = 0,95.

Обробка результатів опосередкованих вимірювань.

Приклад №17

Визначити результат та СКВ випадкової складової похибки опосередкованого вимірювання потужності N = U²/R за даними прямих вимірювань напруги та опору з незалежними випадковими похибками, що розподілені за нормальним законом:

U = (1,00 ± 0,01) B; P = 0,99;

R = (10,0 ± 0,10 ) Ом; Р = 0,997.

Записати результат згідно зі стандартною формою, вказавши довірчий інтервал, в який потрапить результат опосередкованого вимірювання із встановленою ймовірністю Р = 0,99.

Дано:

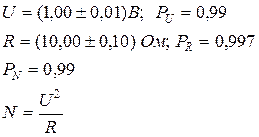
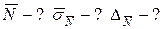
Розв’язок

1. Знайдемо значення математичного сподівання потужності

.

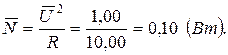2. Визначимо СКВ результату опосередкованого вимірювання потужності

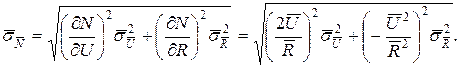
За значеннями нормованої функції Лапласа Ф(z) = P/2 (табл.2) знайдемо значення z та визначимо СКВ результатів прямих вимірювань напруги 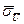і опору .

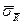Таблиця 2 – Значення нормованої функції Лапласа

z	Ф(z)	z	Ф(z)	z	Ф(z)	z	Ф(z)
0,0	0,00000	1,0	0,14134	2,0	0,47725	3,0	0,49865
0,1	0,03983	1,1	0,36433	2,1	0,48214	3,1	0,49903
0,2	0,07926	1,2	0,38493	2,2	0,48610	3,2	0,49931
0,3	0,11791	1,3	0,40320	2,3	0,48928	3,3	0,49952
0,4	0,15542	1,4	0,41924	2,4	0,49180	3,4	0,49966
0,5	0,19146	1,5	0,43319	2,5	0,49379	3,5	0,49977
0,6	0,22257	1,6	0,44520	2,6	0,49534	3,6	0,49984
0,7	0,25804	1,7	0,45543	2,7	0,49653	3,7	0,49989
0,8	0,28814	1,8	0,46407	2,8	0,49744	3,8	0,49993
0,9	0,31594	1,9	0,47128	2,9	0,49813	3,9	0,49995

Для

.

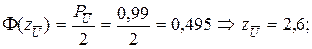
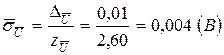Для

.

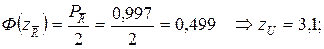
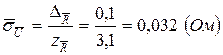Значення СКВ опосередкованого вимірювання потужності складає

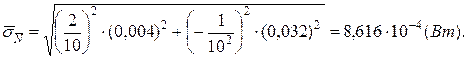
3. Визначимо границі довірчого інтервалу для заданої ймовірності 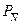= 0,99. Для значення нормованої функції

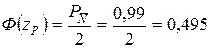
з табл.2 знайдемо значення z_p = 2,6.

Тоді границі довірчого інтервалу будуть становити:

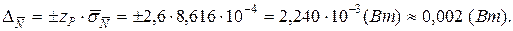
4. Результат опосередкованого вимірювання потужності буде:

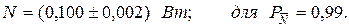
Відповідь: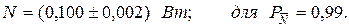

Приклад № 18

Методи фільтрування та іх використання у фармацевтичному аналізі.

Зразок відповіді.

Під процесом фільтрації розуміють розділення гетерогенних сумішей з допомогою пористих мембран, через які, під тиском, проходить рідка фаза (фільтрат), а частинки твердої фази (осад) затримуються на фільтрі.