Химическая кинетика. Химическое равновесие

Химическая кинетика – наука о скоростях и механизмах химических реакций.Объектом изучения является химическая реакция.

Скоростью химической реакции v называют изменение количества вещества (n) в единицу времени (t) в единице реакционного пространства (R). Скорость реакции v = f(c, T, P, kt) – функция различных параметров.

Различают среднюю скорость за какой-то промежуток време-
ни t₁и t₂:

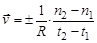
и истинную мгновенную скорость, если промежуток времени бесконечно мал:

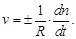
Область, в которой локализован химический процесс (объем V,площадь поверхности S), принято называть реакционным пространством R.

Для гомогенной реакции реакционным пространством является объем V и, если V = const, то

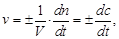
где с – молярная концентрация (моль/л) реагента.

Таким образом, скорость гомогенной реакции – это изменение концентрации одного из веществ в единицу времени. Единица измерения – моль×л^–1×с^–1.

В уравнении скорости знак (+) выбирается в случае, когда скорость реакции измеряется по изменению концентрации продуктов реакции; знак (–), если скорость реакции оценивается по убыли концентрации одного из исходных веществ.

Гетерогенная химическая реакция – протекает на границе раздела фаз. Скорость гетерогенной реакции – изменение количества вещества за единицу времени в единице поверхности (S) раздела фаз:

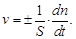
Размерность скорости – моль×м^–2×с^–1.

Все реакции можно разделить на простые и сложные. Простые реакции протекают в одну стадию и называются одностадийными (элементарными).

Сложные реакции представляют собой многостадийный процесс.

В зависимости от числа исходных частиц, участвующих в элементарном акте, говорят о разной молекулярности реакции. Число молекул или других частиц, одновременно взаимодействием которых осуществляется элементарный акт химического превращения, называется молекулярностью реакции. По этому признаку различают моно-, би- и тримолекулярные реакции. Понятие молекулярности применимо только к элементарным актам реакции.

На скорость реакции влияют многие факторы: природа веществ и их концентрация, давление (для газов), температура, катализатор, площадь соприкосновения (для гетерогенных реакций), примеси и их концентрация, форма сосуда (взрывные реакции), реакция среды (рН), внешнее воздействие (g-излучение, электроны, протоны для радиоционно-химических реакций), воздействие УФ и видимого света для фотохимических, природа электродов, электродного потенциала, состава электролита для электрохимических реакций.

Дадим формулировку основного закона химической кинетики:

– скорость реакции в каждый момент времени пропорциональна произведению реагирующих веществ, возведенных в некоторых степенях.

Для необратимой реакции аА + bВ ® сС + dD скорость реакции равна

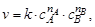
где k – константа скорости реакции; n_A и n_B – коэффициенты, называемые порядками реакции по веществам А и В. Данное уравнение называется основным кинетическим уравнением химической реакции. Оно отражает физический смысл константы скорости реакции. При концентрации реагирующих веществ, равных 1 моль/л, константа скорости численно равна скорости данной реакции. Константа скорости реакции k не зависит от концентрации реагентов, но зависит от их природы, температуры и присутствия катализатора. Размерность k зависит от порядка реакции и определяется из анализа размерностей величин, входящих в основное кинетическое уравнение.

Сумма порядков реакции по продуктам называется порядком реакции n:

n = ån_i ,

где n_i – порядок реакции по i-реагенту.

Для элементарных реакций порядок и молекулярность совпадают.

Величины n_A и n_B могут быть дробными и отрицательными величинами.

Для простых реакций, протекающих в одну стадию, порядок реакции равен сумме стехиометрических коэффициентов:

n = åv_i ,

где v_i – коэффициент перед формулой i-го вещества в уравнении реакции (стехиометрический коэффициент).

Например, если бы реакция аА + bВ ® сС + dD протекала в одну стадию, то n_A = а и n_B = b, тогда кинетическое уравнение принимает вид

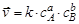и называется законом действующих масс (ЗДМ) для химической кинетики.

ЗДМ справедлив только для элементарных реакций.

Скорость реакции первого порядка характеризуется кинетическим уравнением

.

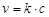Для реакции первого порядка вида А ® продукты скорость реакции в дифференциальной форме выражается уравнением:

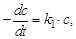
где с – текущая концентрация А, моль/л; k – константа скорости реакции первого порядка, с^-1.

Решение этого уравнения для начального условия с_t=0 = с₀имеет вид

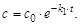
Для оценки степени превращения вещества с/с₀(или отношения текущей концентрации к начальной) часто используют понятие времени (периода) полупревращения ( 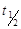) – время, за которое прореагирует половина исходного количества вещества:

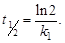
Скорость реакции второго порядка для двух реагентов А и В подчиняется кинетическому уравнению

,

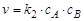где k₂– константа скорости реакции второго порядка, л×моль^–1×с^–1.

При с_А = с_В и если реагируют одинаковые частицы, то v = k₂ × c².

Характер изменения концентрации реагентов во времени может быть выражен уравнением

–dc/dt = k₂ c².

После разделения переменных и интегрирования обеих частей уравнения для начального условия с_t=0 = с₀получаем решение в виде

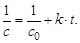
Из данного уравнения с учетом 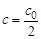получим выражение для времени полупревращения

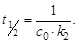
Таким образом, время полупревращения в реакциях второго порядка зависит от начальной концентрации, в отличие от реакций первого порядка. Зависимость периода полупревращения от концентрации определяется порядком реакции.

Зависимость скорости реакции от температуры приближенно выражается уравнением Вант–Гоффа:

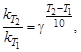
где 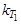и – константы скорости при температурах Т₁ и Т₂; g – тем-пературный коэффициент скорости реакции (коэффициент Вант–Гоф-фа), значение которого для эндотермической реакции выше, чем для экзотермической. Для многих реакциях g лежит в пределах 2…4.

Аналогично для скорости реакции справедливо выражение

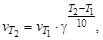
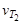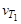где и – скорость реакции при температурах Т₂и Т₁ соответственно.

Шведский ученый С. Аррениус на основании экспериментальных данных показал, что число активных частиц, а следовательно, скорость и константа скорости возрастает с температурой по экспоненциальному закону. Зависимость константы скорости k от температуры Т выражается уравнением Аррениуса:

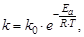
где k₀ – предэкспоненциальный множитель; R – молярная газовая постоянная (8,31 Дж×моль^–1×К^–1); Е_а – энергия активации.

Константа скорости химической реакции определяется долей активных молекул, т.е. числом эффективных соударений

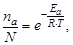
где n_а – число активных молекул; N – общее число молекул.

Уравнение Аррениуса позволяет проводить расчеты изменения скорости реакции с увеличением температуры:

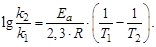
Энергия, необходимая для перехода вещества в состояние активированного комплекса, называется энергией активации.

Уравнение Аррениуса позволяет рассчитать константы скорости (и скорости) реакций при различных температурах, а также энергию

активации и предэкспоненциальный множитель по формулам:

;

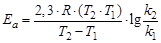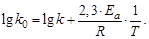
Существует множество реакций, которые не идут до полного превращения реагентов в продукты, взаимодействие как бы прекращается на определенном этапе – т.е. по прошествии некоторого времени изменение концентраций реагентов прекращается. При этом в реакционной смеси обнаруживаются как продукты реакций, так и исходные вещества. Химическая система в таких условиях находится в состоянии так называемого химического равновесия. Условием химического равновесия является равенство прямой и обратной реакций. Реакции, которые при данных условиях одновременно протекают в двух взаимно противоположных направлениях, называют обратимыми.

В условиях химического равновесия концентрации (или парциальные давления в случае газов) исходных веществ и продуктов реакции не изменятся во времени и называются равновесными концентрациями веществ. Равновесные концентрации обозначают символом вещества в квадратных скобках.

Термодинамическим условием химического равновесия является равенство энергии Гиббса химической реакции нулю, т.е. DG = 0.

Для обратимой реакции N₂ + 3H₂ ó 2NH₃ запишем выражение для скорости прямой и обратной реакции синтеза аммиака:

;

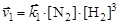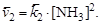
В момент равновесия v₁ = v₂:

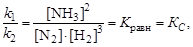
где К_С – константа химического равновесия, выраженная через молярные концентрации веществ.

Для равновесных систем закон действующих масс может быть сформулирован так: химическое равновесие устанавливается, когда произведение концентраций продуктов реакции, возведенных в степени, равные стехиометрическим коэффициентам, деленное на произведение концентраций реагентов, возведенных в соответствующие степени, становится постоянной величиной при определенных условиях.

К_равн является количественной характеристикой химического равновесия. Она не зависит от начальных концентраций реагирующих веществ, но зависит от температуры. Она также не зависит от пути реакции, ее механизма, а определяется только значением равновесных концентраций реагентов и продуктов реакции. Зная величину константы равновесия и исходные концентрации реагентов, можно рассчитать равновесные концентрации всех веществ.

К_равн показывает соотношение констант прямой и обратной ре-акции:

· если К > 1, значит, равновесие смещено в сторону прямой ре-акции;

· если же К < 1, то равновесие смещено в сторону обратной ре-акции.

Если реакция протекает в газовой фазе, то концентрации можно заменить на парциальные давления:

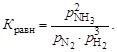
Если поведение всех газообразных реагентов подчиняется законам идеальных газов (р_i = с_i^.RT), то связь между К_с и К_р можно выразить уравнением

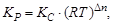
где Dn – изменение числа молей газов в результате реакции.

Для реакции синтеза аммиака:

.

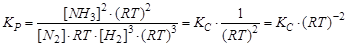При равенстве числа молей слева и справа K_P = K_C .

Между изменением энергии Гиббса и константой равновесия существует соотношение

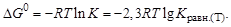
Данное уравнение можно записать в виде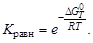

По известным равновесным концентрациям реагирующих веществ можно определить константу равновесия и соответственно стандартную энергию Гиббса химической реакции.

Состояние равновесия характеризуется неизменностью состава реакционной среды во времени. Сместить положение равновесия можно изменением температуры, концентрации участников реакции, иногда общим давлением.

Смещение равновесия подчиняется принципу Ле Шателье:

если изменить условия, при которых система находилась в равновесии (Р, Т, С), то равновесие смещается в сторону той реакции, которая противодействует этому изменению, т.е. способствует восстановлению первоначального состояния.

Примеры решения задач

1. Во сколько раз изменится скорость реакции 2СО(г) + О₂(г) ó
ó 2CO₂(г) при увеличении давления в системе в 10 раз? Температура системы поддерживается постоянной.

Решение. Предположим, что рассматриваемая реакция является элементарной, т.е. для нее справедлив закон действующих масс:

v_нач = k×c²(CO)×c(O₂).

Принимая, что концентрация и парциальное давление связаны прямо пропорциональной зависимостью р_i = с_i^.RT,получаем, что .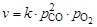

После увеличения давления в системе в 10 раз парциальное давление каждого из реагентов возрастает тоже в 10 раз, т.е.

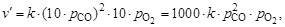
отсюда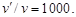

Следовательно, скорость реакции увеличивается в 1000 раз.

2. Реакция при температуре 30 °С протекает за 1,5 мин. За сколько времени закончится эта реакция при температуре 40 °С, если в данном температурном интервале коэффициент скорости реакции равен 3?

Решение. При увеличении температуры с 30 до 40 °С скорость реакции в соответствии с правилом Вант–Гоффа возрастает:

,

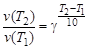где v(T₂), v(T₁) – скорости реакций при заданных температурах 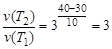,т.е. скорость реакции увеличивается в 3 раза.

В соответствии с определением скорость реакции обратно пропорциональна времени реакции:

,

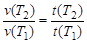где t(Т₂), t(Т₁) – время реакции при температурах Т₁и Т₂.

t(Т₂)= .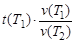

Учитывая, что t(Т₁) = 1,5 мин = 90 с, определяем время реакции при температуре Т₂: t(Т₂) = 30 с. Таким образом, правило Вант–Гоффа соблюдается, что при повышении температуры на каждые 10 °С приводит к повышению скорости химической реакции в 3 раза .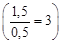

3. Запишите выражение для константы химического равновесия гетерогенной химической реакции H₂(г) + I₂(к) ó 2HI(г). В каком направлении сместится равновесие данной химической реакции при увеличении общего давления в пять раз?

Решение. Константу гетерогенного химического равновесия можно записать через отношение равновесных концентраций или равновесных парциальных давлений газообразных реагентов:

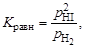или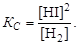

При увеличении общего давления в пять раз парциальные давления газообразных реагентов водорода и иодида водорода увеличатся в пять раз. Скорость прямой реакции при этом увеличится в пять раз, а обратной реакции – в 25 раз. Следовательно, равновесие в данной гетерогенной реакции сместится влево, количество получаемого продукта иодида водорода уменьшится в пять раз.

4. Вычислить равновесные концентрации компонентов в обратимой реакции СО_(г) + Н₂О_(г) ó CO_{2 (г)} + Н_{2 (г)}, если в исходной смеси кон-центрации СО и Н₂О составляли 2 и 3 моль/л соответственно. К_равн= 1.

Решение. Согласно стехиометрическому уравнению составим состав системы во времени в виде таблицы:

Компоненты	СО	Н2О	СО2	Н2
Исходные концентрации			–	–
Прореагировало	х	х	–	–
Образовалось	–	–	х	х
Равновесные концентрации	2 – х	3 – х	х	х

Запишем выражение для константы равновесия:

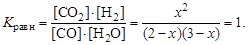
Решая квадратное уравнение получим х = 1,2 моль/л. Поскольку прореагировало 1,2 моль/л СО и Н₂О, то их концентрации к моменту равновесия (равновесные концентрации) составят: [CO] = 2 – 1,2 = 0,8; [H₂O] = 3 – 1,2 = 1,8 моль/л, а равновесные концентрации [H₂] и [CO₂] будут равны по 1,2 моль/л.

5. В реакции первого порядка А ® В + С константа скорости
k₁ = 5×10^–5 с^–1. Определите концентрацию веществ А и В и скорость реакции через 1 ч и через 5 ч, если начальная концентрация А составляла 0,2 моль/л.

Решение. Для реакции 1-го порядка справедливо уравнение

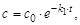
через 1 ч: 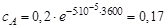моль/л;

через 5 ч: 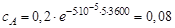моль/л.

Концентрация вещества В находится по стехиометрическому соотношению веществ А и В. Из уравнения реакции следует, что концентрация вещества В возрастет на ту же величину, на какую убывает концентрация А, так как из моль вещества А получается 1 моль В.

Поэтому через 1 час с_В = с_о(А) – с_А = 0,2 – 0,17 = 0,03моль/л;

через 5 ч с_В = с_о(А) – с_А = 0,2 – 0,08 = 0,12моль/л.

Рассчитаем скорость реакции по уравнению:

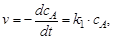
через 1 ч: v = 5 × 10^–5× 0,17 = 8,5×10^-6 моль/л;

через 5 ч: v = 5 × 10^–5× 0,08 = 4×10^-6 моль/л.

6. В реакции второго порядка А + В ® D за 1 ч концентрации веществ А и В уменьшились по сравнению с начальной с_о(А)=с_о(В) =
= 0,2моль/л на 30 %. Определите константу скорости и скорость реакции в начальный момент времени и через 1 ч после начала реакции.

Решение. Концентрации веществ А и В за 1 ч уменьшились на 0,3×с_о = 0,3×0,2 = 0,06 моль/л. Отсюда через час концентрации со-ставляют

с_А = с_В = 0,2 – 0,06 = 0,14моль/л.

Для реакции второго порядка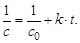

Отсюда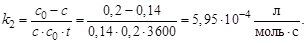

Скорость реакции в начальный момент времени будет равна

v = k₂×[A]×[B] = 5,95×10^–4×0,2×0,2 = 2,38×10^–5 моль×с^–1×л^–1.

Через один час скорость реакции уменьшится и составит

v_t = k₂×[A]×[B] = 5,95×10^–4×0,14×0,14 = 1,16×10^–5моль×с^–1×л^–1.

7. В сосуд объемом 0,1 м³ введено 10 г водорода и 84 г азота.
К моменту достижения равновесия в системе образовалось 34 г ам-миака. Определите константу равновесия реакции К_с.

Решение. Реакция взаимодействия водорода и азота

3H₂(г) + N₂(г) = 2NH₃(г).

Рассчитаем концентрацию реагентов в начальный момент времени. 10 г водорода составляет 5 моль, а 84 г азота – 3 моль. Соответственно концентрации этих веществ будут:

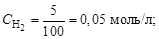
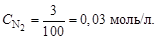
Начальная концентрация продуктов реакции с(NH₃) = 0. К моменту равновесия концентрация аммиака составила:

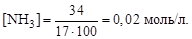
В соответствии со стехиометрической реакцией для образования 0,02 моль/л аммиака должны прореагировать 0,03 моль водорода и 0,01 моль азота. Следовательно, равновесные концентрации этих газов [H₂] = 0,05 – 0,03 = 0,02 моль/л, [N₂] = 0,03 – 0,01 = 0,02 моль/л. Таким образом, константа равновесия

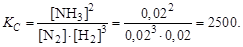
8. Определите константу равновесия реакции N₂O₄(г) = 2NO₂(г)
и направление реакции при 400 К, если в начальном состоянии р(N₂O₄) = 0,5; р(NO₂) = 0,8.

Решение. При расчете стандартного изменения энергии Гиббса DG⁰₄₀₀ пренебрежем зависимостью DН⁰иDS⁰ от температуры:

D_rH⁰ = 2×D_f H⁰₂₉₈(NO₂) – D_f H⁰₂₉₈(N₂O₄) = 2×33,5 – 9,66 = 57,34 кДж,

D_rS⁰ = 2×S⁰₂₉₈(NO₂) – S⁰₂₉₈(N₂O₄) = 2×240,45 – 304,3 = 176,6 Дж/К,

D_rG⁰ = D_rH⁰ + T×D_rS = 57340 – 400 × 176,6 = –13300 Дж.

Константу равновесия определим по уравнению:

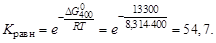
Начальные условия отличаются от стандартных, следовательно, необходимо определить знак DG₄₀₀ для заданных условий. Для этого воспользуемся уравнением:

.

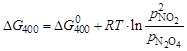Соотношение давлений 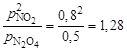существенной меньше К_р = 54,7, поэтому реакция будет протекать в прямом направлении. Кроме этого,

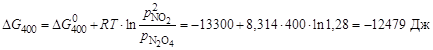
изменение энергии Гиббса отрицательно, следовательно, самопроизвольный процесс из заданного начального состояния возможен только в прямом направлении, т.е. в сторону образования NO₂.