Сутек бойынша Бордың постулаттары

Бордың бірінші постулаты. Қандай да материалдық объектінің центрі жанындағы айналмалы қозғалысы классикалық механика тұрғысынан қарағанда оның қозғалыс моментінің mυr мөлшерімен анықталады және секірмелі өзгеруі керек. Кванттық механика терминінде қозғалыс мөлшерінің моменті 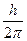арқылы өрнектеледі; ол 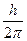немесе 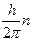түрінде болуы мүмкін. мұнда, n = 1,2,3...∞.

Демек,

mυr = 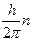. (7)

Бұл жағдай Бордың бірінші постулатының маематикалық теңдігі деп аталады.

Бордың екінші постулаты. Электрон тек квантталған орбитамен қозғалғанда энергиясын жоғалтпайды.

Егер n = 1 болса, онда сутек атомының электроны қалыпты жағдайда болады.

n = 2,3,4…∞ тең болғанда қоздырылған күй деп аталады.

υ (жылдамдық) және r қандай мәнге ие?

Бұл сұраққа жауап беру үшін (7) теңдікке, оған қоса кәдімгі шеңбер бойымен қозғалу жағдайына сүйенеміз: центрден тепкіш күш ( 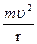) центрге тартқыш күшке ( 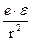) тең болуы керек:

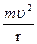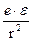= (8)

(7) және (8) теңдіктерді шешіп:

r_{n =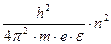} (9)

n = 1,2,3…∞

(9) теңдіктен:

r₁: r₂ : r_3… r_n = 1² : 2² : 3² : … n². (10)

қатынаста болатынын көруге болады.

Осыдан (7) және (8) теңдіктерден r мәнін шығарып тастап, υ_n шешімін табамыз:

υ_n = 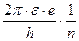. (11)

онда:

υ₁ : υ₂ : υ₃… υ_n = : : 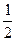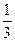… : 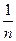(12)

n = 1 υ₁ =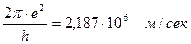

n = 2 υ₂ = 2,187 · 10⁶ 1/2 м/сек және т.б.

Бордың үшінші постулаты.Электрон алыс орбитадан жақын орбитаға ауысқанда энергия квантын жоғалтады.

Демек,

Е_алыс – Е_жақ = hν. (13)

ν = 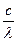или 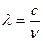. (14)

(1.7) және (1.8) теңдеулерден:

ν = 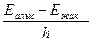(15)

немесе

Е_алыс – Е_жақ = 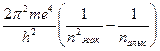= hν. (16)

ν = 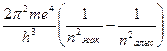гц. (17)

Тұрақты шамалардың бәрін қойсақ,

ν = 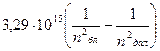гц. (18)

1900 жылы Макс Планк электромагнитті сәулеленудің кванталған, яғни электромагнитті сәулелену кванттармен жұтылады, немесе сәулеленеді және мына қатынаспен аныкталатындығын болжаған:

Е = h υ(19)

1905 жылы Альберт Эйнштейн Планктың болжамын дәлелдеген, яғын ол квант энергиясы

Е = m с²(20)

тендігімен анықталатындығын дәлелдеген.

Мұнда: Е – энергия, Джоуль (Дж);

Һ = 6,626 • 10^-34 Дж•с, Планк тұрақтысы;

ν– жиілік, (с −немесе герц (Гц)).

Электромагниттік сәулеленуді сипаттау ұшін екі көзқарас пайдаланылады:

1. толқындық− монохроматты сәулелену толқын сияқты таралады және толқын ұзындығымен (λ)және тербеліс жиілігімен (ν) сипатталады;

2. корпускулалық – электромагнитті сәулелену микробөлшектерден - фотондардан тұрады, квант энергиясының тасымалдаушысы фотондар болады.

Кейіннен зерттеулер нәтижесінде электромагнитті сәулеленуге дифракция, интерференция қасиеттері, яғни бұл толқындық қасиеттері, тән екені дәлелденген. Сонымен қатар, олардың массасы, энергиясы бар, олар қысымдық әсер ететіндігі анықталған - бұл бөлшектердің қасиеті.

Кейіннен 1924 жылы Луи де Бройль корпускулалық – толқындық көзқарастарды барлық микробөлшектерге таратып математикалық түрде ол байланысты төмендегі теңдікпен көрсеткен - бұл теңдік де Бройль қатынасы деп аталады:

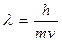(21)

Теңдік толқын ұзындығы мен масса және бөлшектің жылдамдық арасындағы байланысты дәлелдейді.

Оны Планк Е = hv (19) мен Эйнштейн Е = mс² (20)теңдіктерін салыстырып та алуға болады, яғни:

h v = m с² , (22)

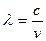, онда 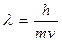(23)

Электронның екі түрлі қасиеті болғандықтан, яғни бөлшектің және толқынның, оның ядро маңайында дәл координатын және қозғалыс мөлшерінің моментін анықтау мүмкін емес. Бұл құбылыс Гейзенбергтің анықталмаған принципі деп аталады.

Анықталмағандық принципі. В. Гейзенберг (1927) анықталмағандық принципін ұсынды: бірмезгілде микробөлшектің күйін (оның координатын) және қозғалыс мөлшерін (импульсін ρ = mυ) нақты анықтау мүмкін емес.

Анықталмағандық принципінің математикалық өрнегі келесі түрге ие:

ΔхΔρ ≥ 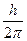немесе Δх Δυ ≥ 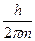, (24)

мұндағы Δх, Δρ, Δυ – бөлшектің жылдамдығына, импульсіне және анықталмағандық жағдайына сәйкес келеді.

(24) теңдік бөлшектің координаты (анықталмағандық Δх неғұрлым аз) неғұрлым нақтырақ анықталған болса, соғұрлым жылдамдық (Δυ) аз анықталған болады және керісінше импульс неғұрлым нақты анықталған болса, бөлшектің орналасу орны соғұрлым көбірек анықталмаған болады.

Сонымен егер электрон орналасуы нақты 10^-12м бастап анықталған болса, онда анықталмағандық 58 000 км/с жылдамдықты құрайды.

Атомның (молекуланың) берілген орнында электронның болу мүмкіндігін және оның энергиясын есептеу - күрделі математикалық мәселе. Ол Шредингердің толқындық функциясы деп аталатын теңдікпен шешіледі.

Шредингер теңдеуі толқындық функцияны 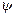электронның потенциал энергиясы U мен оның толық энергиясын Е байланыстырады:

,

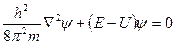мұндағы бірінші мүше электронның кинетикалық энергиясына сәйкес келеді;

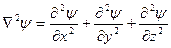- х, у және z координаталары бойынша толқындық функцияның 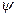екінші туындысының қосындысы, m – электрон массасы, h – Планк тұрақтысы.

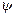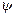Толқындық теңдеудің математикалық мағынасын айқындамай-ақ, оның шешімін электрон энергиясының толық анықталған дискреттік мәні деуге болады. Толқындық теңдеу шешімі деп аталатын әртүрлі функциялар ₁, ₂, 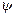₃,..., энергияның өзіндік мәніне Е₁, Е₂, Е₃,..., Е_n сәйкес келеді.

Толқындық функция, орбиталь деп аталатын Шредингер шешімі болады.

КВАНТ САНДАРЫ

Атомдық орбиталь үш квант санымен ( 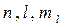), ал электрон – төрт квант санымен сипатталады ( ).

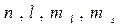Бас квант саны (n) электронның энергетикалық деңгейін сипаттайды, n – оң бүтін сандар болады, бірден шексіз санға дейін болуы мүмкін n =1,2,3 . . . ∞.

Энергетикалық деңгейлерді бас әріппен де белгілейді:

n
	К	L	M	N	O	P

Энергетикалық деңгейлерді кейде энергетикалық қабаттар деп атайды. Энергетикалық деңгей саны химиялық элемент атомы орналасқан период номерімен аңықталады.

Период	Энергетикалық деңгей саны
I
II
III
IV

Энергетикалық деңгейдегі максимал электрон саны төмендегі теңдеумен өрнектеледі:

N = 2 n²

n = 1	N = 2 • 12 = 2	1s2	2е
n = 2	N = 2 • 22 = 8	1s2 2s2 2p6	8е
n = 3	N = 2 • 32 =18	1s2 2s2 2p6 3s2 3p6 3d10	18е

Кванттау ережесі бойынша электрон атомда белгілі кванттық күйде болады және оның энергиясы төмендегі қатынаспен анықталады:

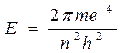(25)

мұнда m – электрон массасы;

е – электрон заряды;

һ – Планк тұрақтысы;

n – бас квант саны.

Егерде алдындағы теңдікке барлық белгілі тұрақтыларды қойса, онда мына қатынасты алуға болады:

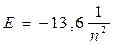(эВ) (26)

Электронның бір энергетикалық күйден екінші энергетикалық күйге ауысуы энергияның күрт өзгеруімен байланысты. График түрде оны былай сипаттауға болады.