Водные растворы сильных электролитов
Для сильных электролитов изотонический коэффициент теоретически должен быть равен числу ионов, на которые распадается молекула при диссоциации: при α = 1 i = ν (например, для KCl и NH4Cl ν = 2, для K2SO4 и CuCl2 ν = 3, для AlCl3 ν = 4 и т.д.). Однако обычно экспериментальные величины i < ν .
Поведение сильных электролитов в растворах не соответствует их полной ионизации, что обнаруживается экспериментально. Так, для растворов хлорида натрия, который полностью распадается на ионы, следовало бы ожидать, что изотонический коэффициент i = 2. Однако этого не наблюдается. Только в предельно разбавленных растворах NaCl значение i приближается к двум. Эквивалентная электропроводность растворов сильных электролитов не остается постоянной при изменении концентрации, как этого можно ожидать при полной диссоциации, а увеличивается при разбавлении растворов.
Особенности поведения сильных электролитов обусловлены тем, что ионы в растворе взаимодействуют благодаря наличию значительных электростатических сил. Взаимодействие усиливается с ростом концентрации электролита в растворе, т. е. с уменьшением расстояния между ионами. Взаимодействие противоположно и одноименно заряженных ионов (соответственно притяжение и отталкивание) приводит к тому, что вблизи каждого иона находятся преимущественно ионы с противоположным зарядом, образующие т.н. ионную атмосферу. В системе создаются условия для равномерного размещения ионов подобно их положению в кристаллах, но в более удаленных друг от друга положениях. Радиус ионной атмосферы сравнительно велик, поэтому ионные атмосферы соседних ионов пересекаются; кроме того, каждый ион окружен дипольными молекулами растворителя - сольватной оболочкой, что также отражается на их свойствах и свойствах растворителя. Таким образом, в растворе сильного электролита возникает подобие пространственной структуры, что ограничивает свободу перемещения ионов и приводит к изменению свойств раствора в том же направлении, как действовало бы уменьшение степени диссоциации. Поэтому, определяя степень диссоциации раствора сильного электролита, получают так называемую кажущуюся степень диссоциации, т.е. величину α с поправкой на межионное взаимодействие. Чем выше концентрация раствора, тем сильнее взаимодействие ионов Поэтому с повышением концентрации сильных электролитов в растворе даже при полной их диссоциации свойства раствора изменяются аналогично тому, как если бы уменьшалась степень диссоциации электролита.
Бьеррум и Семенченко для растворов сильных электролитов ввели понятие “ионная пара”. Так как с увеличением концентрации сильного электролита в растворе увеличивается взаимное притяжение разноименных ионов, что при достаточном приближении их друг к другу приводит к образованию ионных пар. Они ведут себя подобно молекулам, хотя и не являются ими. Отличие от молекул у них в том, что ионы в них непосредственно друг с другом не соприкасаются, а разделены одним или несколькими слоями молекул воды. Образование ионных пар воспринимается на опыте как отсутствие полной диссоциации сильного электролита.
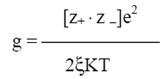 |
Для каждого электролита существует параметр Бьеррума g, представляющий собой расстояние, на которое подходят друг к другу ионы в процессе образования ионной пары. Его определяют из соотношения
где z+ и z– – заряды катиона и аниона; e – заряд электрона (4.8·10–10 эл.ст.ед.); К – постоянная Больцмана (1,38·10–16 эрг/град = 1,38·10–23 Дж/К); Т – абсолютная температура; ξ – диэлектрическая проницаемость растворителя.
При увеличении заряда иона увеличивается g, т.е. увеличивается расстояние, на котором взаимодействуют ионы. При увеличении ξ уменьшается электростатическая сила взаимодействия ионов. Поэтому полярные растворители, характеризующиеся большими значениями диэлектрической постоянной, способствуют образованию растворов, являющихся сильными электролитами. При увеличении температуры g падает, и взаимодействие между ионами ослабевает. Параметр Бьеррума имеет вполне определенное значение для каждого растворителя при заданных значениях температуры и зарядов ионов. Так, для одновалентных ионов в воде при Т = 298 К g = 3,57·10-8= 3,57°A.
Тогда при g < 3,57 °A молекула считается недиссоциированной, при g 3,57°A ионы можно считать изолированными.
Для оценки состояния ионов сильных электролитов в растворе пользуются величиной, называемой активностью. Данное понятие введено американским ученым Г. Льюисом в 1907 г. Эта характеристика компонента, которая связана с другими термодинамическими величинами (∆G и др.) так же, как в идеальном растворе связана с ними концентрация. Иными словами, под активностью иона понимают ту эффективную условную концентрацию его, соответственно которой он действует в химических реакциях. Активность количественно отражает взаимодействия ионов между собой и с молекулами растворителя. Введение понятия об активности не раскрывает механизма процессов этих взаимодействий. Это лишь удобный прием, позволяющий определять свойства любых растворов. Активность а связана с аналитической концентрацией С следующим уравнением
a = f·С,
где a – активность раствора, f – коэффициент активности.
Коэффициенты активности различных ионов различны. Кроме того, они изменяются при изменении концентрации раствора. В концентрированных растворах f обычно меньше единицы, а с разбавлением раствора он приближается к единице. Значение f < 1 указывает на взаимодействие между ионами, приводящее к их связыванию. В очень разбавленных растворах расстояние между ионами достаточно велико, действие межионных сил мало, и f ≈ 1.
Активности индивидуального иона для катионов и анионов обозначаются соответственно как а+ и а–; определяются они следующим образом:
a+ = f+ С + ; а– = f– С –
Средняя ионная активность симметричного электролита a± равна
a± = (a+ а–)1/2
Коэффициент средней ионной активности определяется как
f± = (f+ f–)1/2
Для несимметричного электролита Сν+Аν−, который диссоциирует на ν+ положительных ионов и ν− отрицательных ионов, средняя активность a± равна
a± = [(a+)ν+ (а–)ν−]1/ν,
а средний коэффициент активности f± равен
f± = [(f+)ν+ (f–)ν−]1/ν
Хотя коэффициенты активности индивидуального иона нельзя измерить непосредственно, коэффициенты средней ионной активности можно определить с достаточной степенью точности. Исходя из измеренных коэффициентов средней ионной активности, с помощью различных методов можно вывести полуэмпирические значения коэффициентов активности индивидуальных ионов.
В разбавленных растворах природа иона мало влияет на значение f. Поэтому считают, что коэффициент активности данного иона зависит только от его заряда и от ионной силы раствора I. Ионная сила раствора – это мера интенсивности электрического поля, создаваемого ионами в растворе. Ионная сила – это полусумма произведений концентраций всех ионов, находящихся в растворе, на квадрат их заряда:
I = 1/2(C1z12 + C2z22 + ... + Cnzn2).
Для одно, одновалентных (1,1 – электролитов) (z+ = z− = 1) ионная сила равна концентрации электролита в растворе.
Для очень разбавленных растворов сильных электролитов в одном и том же растворителе эмпирически устанавлен закон ионной силы: во всех растворах в данном растворителе с одинаковой ионной силой коэффициент активности иона одинаков независимо от типа других присутствующих в растворе ионов.
Понятие ионной силы полезно при сравнении растворов различного состава, так как позволяет учесть электростатическое взаимодействие разноименных ионов. Поскольку электростатическое взаимодействие ионов представляет собой функцию квадрата их заряда, ионная сила является более полезным критерием поведения раствора, чем его концентрация. Хотя ионную силу нельзя рассматривать как панацею от всех бед, однако с ее помощью можно избежать ошибок, связанных с игнорированием частного взаимодействия между составными частями раствора. При определении ионной силы приходится прибегать к ряду допущений. При расчете ионной силы мы должны знать главные ионы, присутствующие в растворе. Если путем теоретических или экспериментальных исследований установлено присутствие и других компонентов, их также нужно ввести в расчет значения ионной силы.
На рис. 16 представлены типичные кривые, отражающие зависимость между экспериментально измеряемыми средними коэффициентами активности и ионной силой. Эта диаграмма показывает влияние валентности на величину коэффициента активности. Так, одно-одновалентная соль КСl имеет наибольшую величину коэффициента активности; для солей Nа2SO4 и СuСl2, представляющих собой соединения двухвалентного иона с двумя одновалентными, кривые совпадают до значения ионной силы 0,1; двух-двухвалентная соль СuSO4 характеризуется наименьшим коэффициентом активности.
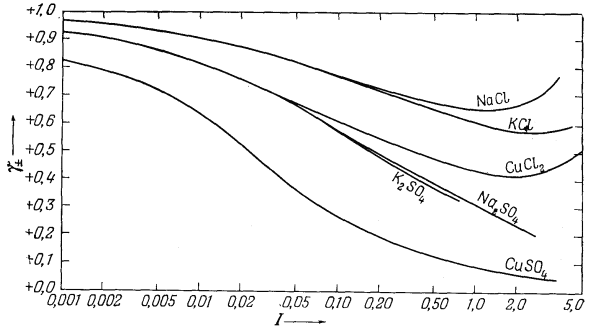
Рис. 16. Зависимость средних коэффициентов активности некоторых типичных солей от ионной силы раствора (шкала логарифмическая).
Как уже упоминалось, существует возможность точного экспериментального определения коэффициентов средней ионной активности, однако коэффициент активности индивидуального иона непосредственно измерить нельзя. Это затруднение можно обойти, допустив, что для стандартного 1,1–электролита f+=f– в условиях интересующих нас значений ионной силы. Основой расчета коэффициентов активности индивидуального иона служит поведение КСl в растворе. Различными способами доказано, что в этом случае fK+ и fCl– имеют одинаковые значения. Отсюда мы можем вывести приближенное равенство
f±КСl = [((f+)1/2 (f–)1/2)]1/2 = fK+ = fCl–
Используя это соотношение, по имеющимся коэффициентам средней ионной активности можно составить таблицу значений коэффициентов активности индивидуальных ионов.
Так, для одновалентного хлорида
f±MСl = [(fM+)·(fCl–)]1/2 = [(fM+)·(f±KСl)]1/2,
fM+ = f±2МСl2 / f±2КСl
Для двухвалентного хлорида
f±2МСl2 = [(fM2+)·(fCl–)2]1/3 = [(f±M2+)·(f±KСl)2]1/3,
fM2+ = f±3МСl2 / f±2КСl
Для прочих солей калия можно использовать обратную зависимость и получить коэффициенты активности анионов. Например,
f±K2SO4 = [(fK+)2 (fSO42–)]1/3 = [(f±KСl)2 (fSO42–)]1/3,
fSO42– = f±3K2SO4 / f±2КСl
Чтобы определить fCu2+ для солей типа СuSO4, необходим более сложный расчет. Сначала составим уравнение
f±CuSO4 = [(fCu2+)·(fSO42–)]1/2,
а затем, подставив значение fSO42–и сделав соответствующие преобразования, найдем
fCu2+ = [(f±2 CuSO4)·(f±2КСl) / f±3K2SO4
Подобный способ вычисления коэффициентов активности индивидуального иона по коэффициентам средней активности называют среднесолевым методом (mean salt method).
П.Дебаем и Г.Хюккелем (1923) была разработана количественная теория сильных электролитов. Уравнение Дебая - Хюккеля, определяющее коэффициент активности индивидуального иона в разбавленных растворах, выглядит следующим образом:
–lg fi = (A zi2I1/2) / (1 + а°iBI1/2)
Значения zi и I этого уравнения были указаны при определении понятия ионной силы; А и В - характеристические константы растворителя при данных температуре и давлении. В табл. 7 приведены значения А и В для воды как функции температуры (при давлении 1 атм).
Таблица 7.
Значения констант А и В из уравнения Дебая-Хюккеля (водный раствор)
| Температура, °С | А | В (´10-8) | Температура, °С | А | В (´10-8) |
| 0,4883 | 0,3241 | 0,5175 | 0,3297 | ||
| 0,4921 | 0,3249 | 0,5221 | 0,3305 | ||
| 0,4960 | 0,3258 | 0,5271 | 0,3314 | ||
| 0,5000 | 0,3262 | 0,5319 | 0,3321 | ||
| 0,5042 | 0,3273 | 0,5371 | 0,3329 | ||
| 0,5085 | 0,3281 | 0,5425 | 0,3338 | ||
| 0,5130 | 0,3290 |
Величина множителя а°i зависит от "эффективного диаметра" данного иона в растворе и преимущественно определяется экспериментальным путем. Список значений а°i (для разных ионов) приведен в табл. 8. Физический смысл величины а°i которая обычно связывается с диаметром данного иона в растворе, заслуживает краткого разъяснения. Значения как правило, превышают а°i величину ионных диаметров, установленную для ионов в кристаллах. Вероятно, эта разница возникает за счет оболочки из молекул воды, которые окружают данный ион в растворе. Были предприняты попытки структурной интерпретации величины а°i, однако четкого представления относительно координации молекул воды вокруг заряженных ионов до сих пор не выработано.
Таблица 8.
Величина а°i для некоторых индивидуальных ионов в водных растворах
| а°i (´108) | Ионы |
| 2,5 | Rb+, Cs+, NH+4 T1+, Ag+ |
| 3,0 | K+, Cl‾, Br‾, I‾, NO3‾ |
| 3,5 | OH‾, F‾, HS‾, ВrO3‾, IO4‾, МnО4‾ |
| 4,0-4,5 | Na+, НСО3‾, H2PO4‾, НSO3‾, Hg22+, SO42‾, SeO42‾, CrO42‾, HPO42‾, PO43‾ |
| 4,5 | Pb2+, CO32‾, SO32‾, MoO42‾ |
| 5,0 | Sr2+, Ba2+, Ra2+, Cd2+, Hg2+, S2‾, WO42‾ |
| Li+, Ca2+, Cu2+, Zn2+, Sn2+, Mn2+, Fe2+, Ni2+, Co2+ | |
| Mg2+, Be2+, | |
| H+, Al3+, Сr3+, трехвалентные редкие земли | |
| Th4+, Zr4+, Ce4+, Sn4+ |
Теория Дебая – Хюккеля применима только при концентрациях, не превышающих 0,05 моль/л. Наилучшим методом определения активности индивидуального иона в растворах с ионной силой, превышающей 0,05, считается среднесолевой метод. В растворах с меньшей ионной силой среднесолевой метод и расчеты по уравнению Дебая - Хюккеля обычно дают сходные результаты; с помощью уравнения Дебая - Хюккеля, кроме того, можно проводить экстраполяцию в область бесконечного разбавления. Если величина ионной силы становится очень низкой, то для бинарного электролита приведенное выше уравнение Дебая - Хюккеля сокращается до следующего предельного выражения:
–lg fi = A zi2I1/2
Или для водных растворов при температурах, близких к комнатным:
–lg fi = 0,5 zi2I1/2
То же выражение для среднего коэффициента активности электролита, образованного лишь двумя различными ионами, в предельном случае бесконечно разбавленного раствора выглядит следующим образом:
–lg f± = A|z+· z–|I1/2
(символ | | обозначает абсолютную величину).
На рис. 17 приведены значения коэффициентов активности индивидуального иона для некоторых обычных ионов, определенные среднесолевым методом и вычисленные по уравнению Дебая - Хюккеля. При анализе рисунка следует обратить внимание на то, что значения fi для всех одновалентных ионов быстро сближаются как друг с другом, так и с предельными величинами, вычисленными по теории Дебая - Хюккеля; это сближение происходит при значениях ионной силы, меньших примерно 0,02. За исключением иона NO3‾, значения коэффициентов активности, рассчитанные по теории Дебая - Хюккеля и по среднесолевому методу, достаточно близко совпадают вплоть до ионной силы I = 0,1. Значения коэффициентов активности для двух двухвалентных ионов SO42‾ и Са2+ больше различаются между собой и более далеки от значений по Дебаю - Хюккелю. Однако практически можно считать, что величины коэффициентов активности индивидуального иона, рассчитанные этими двумя методами, достаточно близко совпадают при ионной силе раствора, не превышающей примерно 0,05.
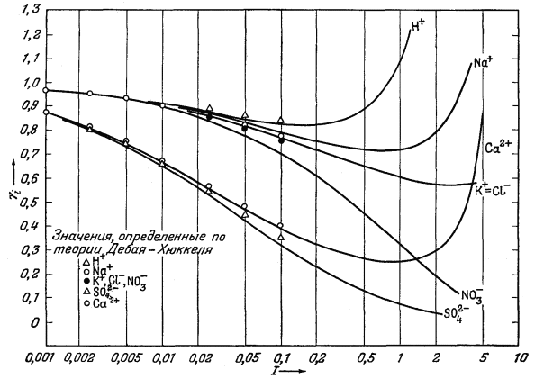
Рис. 17 . Зависимость коэффициентов активности индивидуальных ионов от ионной силы раствора для некоторых обычных ионов. Сплошными линиями показаны значения, рассчитанные среднесолевым методом. При I < 0,01 значения fi, рассчитанные по методу Дебая - Хюккеля, для всех рассматриваемых одновалентных ионов одинаковы (в пределах ошибки эксперимента).
