Рекомендации к оформлению лабораторной работы
Оформление лабораторной работы должно осуществляться следующим образом:
1. Название.
2. Цель.
3. Основные теоретические положения, схема установки, расчетные уравнения.
4. Экспериментальная часть:
1) Последовательность выполнения работы.
2) Запись измерения температур во время опыта :
| Время от начала опыта, мин. | Предварительный период | Главный период | Заключительный период | ||||||
| t0C |
4. Обработка экспериментального материала:
1) Построение графика,
2) Результаты вычислений.
5. Вывод.
З А Н Я Т И Е № 4
Т Е М А: «ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЭНТРОПИЯ И ЕЕ ИЗМЕНЕНИЕ В РАЗЛИЧНЫХ ПРОЦЕССАХ».
I. МОТИВАЦИЯ ЦЕЛИ:
Второй закон термодинамики – закон о возможности протекания самопроизвольных процессов. Он устанавливает критерии необратимости термодинамических процессов. На его основании можно предсказать, при каких внешних условиях возможен процесс и в каком направлении он будет протекать, что представляет большой практический и теоретический интерес.
Третий закон термодинамики – закон об абсолютном значении энтропии, который был сформулирован уже в начале XX столетия. На его основе можно вычислить константу равновесия химической реакции, а следовательно, и максимально возможный выход продукта реакции, не прибегая к опытному ее определению ни при одной из температур.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
1. Усвоить содержание II и III начал термодинамики, знать их различные характеристики.
2. Научиться рассчитывать абсолютную и стандартную энтропии, изменение энтропии в различных физико-химических процессах.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ:
a. Понятие о термодинамических функциях состояния, системах, параметрах.
b. Первый закон термодинамики.
c. Приемы дифференцирования и интегрирования.
IV. П Л А Н И З У Ч Е Н И Я Т Е М Ы:
1. Самопроизвольный процесс. Признаки самопроизвольного процесса.
2. Равновесные и неравновесные процессы.
3. Обратимые и необратимые процессы. Критерии термодинамически обратимого процесса.
4. Тепловая машина Карно. КПД тепловой машины. Цикл Карно как основа II начала термодинамики.
5. Второй закон термодинамики: словесные формулировки и математические уравнения, его выражающие. Статистическая природа II начала термодинамики.
6. III закон термодинамики. Абсолютная и стандартная энтропии.
7. Тепловая теорема Нернста.
8. Энтропия – определение понятию. Многоплановый смысл и свойства энтропии:
- функция состояния;
- мера «связанной энергии»;
- мера необратимости процесса;
- мера неупорядоченности в системе;
- критерий направленности и предела самопроизвольного процесса в изолированных системах.
9. Связь энтропии с термодинамической вероятностью системы в данном состоянии – уравнение Больцмана. Статистический характер энтропии.
10. Изменение энтропии в обратимом и необратимом процессах для изолированной и неизолированной систем.
11. Расчет изменения энтропии в различных процессах.
12. Связь I и II законов термодинамики.
V. ЛИТЕРАТУРА:
1. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 15-18, 35-42.
2. Киреев В. А. Краткий курс физической химии М. 1978, с. 202-217.
3. К.С. Краснов Физическая химия. - М., Высшая школа, 2001, с. 235-241, 251-260.
4. Стромберг А. Г., Семченко Д.П., Физическая и коллоидная химия, М. 1999, с. 81-93.
5. Лекционный материал
VI. В О П Р О С Ы Д Л Я С А М О К О Н Т Р О Л Я:
1. Дайте определение энтропии, исходя из соотношения

2. Напишите математическое соотношение между изменением энтропии и теплотой необратимого процесса, протекающего в неизолированной системе.
3. Как изменяется энтропия в изолированной системе при самопроизвольном течении процесса?
4. В каком соотношении находятся молярные энтропии трех агрегатных состояний одного вещества: газа, жидкости и твердого тела?
5. В изолированной системе самопроизвольно протекает химическая реакция с образованием некоторого количества конечного продукта. Как изменяется энтропия системы?
6. Как изменяется энтропия:
а) при кристаллизации 1 моль жидкой воды;
б) при плавлении 1 моль льда;
в) при нагревании 1 моль воды от 20 ОС до 50 ОС.
7. Приведите уравнение для расчета изменения энтропии 1 моль бензола при нагревании его от 0 ОС до 20 ОС. Температура плавления бензола 5,5 ОС.
8. Как изменяется энтропия изолированной системы, в которой обратимо кристаллизуется вещество?
9. Дайте определение:
а) абсолютной энтропии;
б) стандартной энтропии.
10. Приведите уравнение Больцмана, устанавливающее связь между энтропией и термодинамической вероятностью состояния системы.
11. Приведите толкование понятия "связанная энтропия" (TS).
12. Как изменяется связанная энергия системы TS при:
а) нагревании газа;
б) при конденсации водяного пара в жидкость?
Ответ обосновать.
13. К какому значению стремится энтропия правильно образованного кристалла при приближении температуры к абсолютному нулю.
14. Напишите математическое выражение второго закона термодинамики для бесконечно малого изменения состояния в обратимом и необратимом процессах, протекающих в неизолированной системе.
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 4-1 Рассчитайте изменение энтропии при нагревании 0.7 моль моноклинной серы от 25 до 200 оС при давлении 1 атм. Мольная теплоемкость серы равна:
Cp(Sтв) = 23.64 Дж/(моль. К),
Cp(Sж) = 35.73 + 1.17. 10-3. T Дж/(моль. К).
Температура плавления моноклинной серы 119 оС, удельная теплота плавления 45.2 Дж/г.
Решение. Общее изменение энтропии складывается из трех составляющих: 1) нагревание твердой серы от 25 до 119 оС, 2) плавление, 3) нагревание жидкой серы от 119 до 200 оС.
 4.54 Дж/К.
4.54 Дж/К.
 2.58 Дж/К.
2.58 Дж/К.

 S =
S =  S1 +
S1 +  S2 +
S2 +  S3 = 11.88 Дж/К.
S3 = 11.88 Дж/К.
Ответ. 11.88 Дж/К.
Пример 4-2. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от объема V1 до объема V2: а) обратимо; б) против внешнего давления p.
Решение. а) Изменение энтропии газа при обратимом изотермическом расширении можно найти с помощью термодинамического определения энтропии с расчетом теплоты расширения по первому закону:
 .
.
Так как расширение обратимое, то общее изменение энтропии Вселенной равно 0, поэтому изменение энтропии окружающей среды равно изменению энтропии газа с обратным знаком:
 .
.
б) Энтропия - функция состояния, поэтому изменение энтропии системы не зависит от того, как совершался процесс - обратимо или необратимо. Изменение энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело - энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе:
 .
.
В этом выводе мы использовали тот факт, что  U = 0 (температура постоянна). Работа, совершаемая системой против постоянного внешнего давления равна: A = p(V2-V1), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.
U = 0 (температура постоянна). Работа, совершаемая системой против постоянного внешнего давления равна: A = p(V2-V1), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.
Общее изменение энтропии газа и окружающей среды больше 0:
 ,
,
как и полагается для необратимого процесса.
Пример 4-3.Расчитайте изменение энтропии 1000 г воды в результате ее замерзания при -5 ОС. Теплота плавления льда при 0оС равна 6008 Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3 Дж/(моль. К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс - самопроизвольный.
Решение. Необратимый процесс замерзания воды при температуре -5 ОС можно представить в виде последовательности обратимых процессов: 1) нагревание воды от -5 ОС до температуры замерзания (0 ОС); 2) замерзание воды при 0 ОС; 3) охлаждение льда от 0 до -5 ОС:

Изменение энтропии в первом и третьем процессах (при изменении температуры) рассчитывается по формуле (4.9):
 77.3 Дж/К.
77.3 Дж/К.
 -35.6 Дж/К.
-35.6 Дж/К.
Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода (4.13). Необходимо только иметь в виду, что теплота при замерзании выделяется:
 -1223 Дж/К.
-1223 Дж/К.
Т.к. энтропия - функция состояния, общее изменение энтропии равно сумме по этим трем процессам:
 S =
S =  S1 +
S1 +  S2 +
S2 +  S3 = -1181 Дж/К.
S3 = -1181 Дж/К.
Энтропия при замерзании убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при замерзании воды возрастает, как и полагается в необратимом процессе.
Ответ. -1181 Дж/К.
4-1. Приведите пример термодинамического процесса, который может быть проведен как обратимо, так и необратимо. Рассчитайте изменение энтропии системы и окружающей среды в обоих случаях.
4-2. Рассчитайте изменение энтропии при образовании 1 м3 воздуха из азота и кислорода (20 об.%) при температуре 25 оС и давлении 1 атм.
4-3. Рассчитайте мольную энтропию неона при 500 К, если при 298 К и том же объеме энтропия неона равна 146.2 Дж/(моль. К).
4-4. Рассчитайте изменение энтропии при нагревании 11.2 л азота от 0 до 50 оС и одновременном уменьшении давления от 1 атм до 0.01 атм.
4-5. Один моль гелия при 100 оС и 1 атм смешивают с 0.5 моль неона при 0 оС и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм.
4-64-7. Три моль идеального одноатомного газа (CV = 3.0 кал/(моль. К)), находящегося при T1 = 350 K и P1 = 5.0 атм, обратимо и адиабатически расширяются до давления P2 = 1.0 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии, энтальпии и энтропии в этом процессе.
4-8. Рассчитайте изменение энтропии при нагревании 0.4 моль хлорида натрия от 20 до 850 оС. Мольная теплоемкость хлорида натрия равна:
Cp(NaClтв) = 45.94 + 16.32. 10-3. T Дж/(моль. К),
Cp(NaClж) = 66.53 Дж/(моль. К).
Температура плавления хлорида натрия 800 оС, теплота плавления 31.0 кДж/моль.
4-9. Рассчитайте изменение энтропии при смешении 5 кг воды при 80 оС с 10 кг воды при 20оС. Удельную теплоемкость воды принять равной: Cp(H2O) = 4.184 Дж/(г. К).
4-10.Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 оС, к 200 г воды (90 оС) в изолированном сосуде. Теплота плавления льда равна 6.0 кДж/моль.
4-11. Запишите выражение для расчета абсолютной энтропии одного моль воды при температуре 300 0С и давлении 2 атм.
4-12. Нарисуйте график зависимости стандартной энтропии воды от температуры в интервале от 0 до 400 К.
4-13. Рассчитайте изменение энтропии 1000 г метанола в результате его замерзания при -105 ОС. Теплота плавления твердого метанола при -98 оС (т.пл.) равна 3160 Дж/моль. Теплоемкости твердого и жидкого метанола равны 55.6 и 81.6 Дж/(моль. К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс - самопроизвольный.
4-14.Пользуясь справочными данными, рассчитайте стандартное изменение энтропии в реакции H2(г) + ЅO2(г) = H2O(г) а) при 25 оС; б) при 300 оС.
4-15. Теплоемкость некоторого вещества в интервале температур от T1 до T2 изменяется следующим образом:

Постройте график зависимости энтропии вещества от температуры в этом интервале температур.
4-16. Пользуясь справочными данными, приведите пример самопроизвольной химической реакции, для которой стандартное изменение энтропии меньше 0.
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
5. Выполнение лабораторной работы “Определение теплоты растворения хорошо растворимой соли”
Лабораторная работа№2
«Определение теплоты растворения хорошо растворимой соли».
При растворении соли в жидкости имеют место два процесса: разрушение кристаллической решетки – эндотермический процесс и сольватация (гидратация) ионов - экзотермический процесс. В зависимости от соотношения этих тепловых эффектов, которое определяется природой растворенного вещества и растворителя, теплота растворения соли может быть как положительной (DН > 0), так и отрицательной (DН < 0) величиной.
Выделяют понятие интегральная теплота растворения – тепловой эффект растворения 1 моль вещества в таком количестве растворителя, который образует раствор определенной моляльности (b).
| ВИД ДЕЙСТВИЯ | СПОСОБ ДЕЙСТВИЯ |
| 1. Собрать калориметр и провести «предварительный период» калориметрического опыта. | 1. Смотреть 1 и 2 этапы работы предыдущего занятия. |
| 2. Провести «главный» и «заключительный периоды» калориметрического опыта. | 1. На 5-й минуте опыта, не отключая мешалку и секундомер, открыть пробку и быстро всыпать 5 г хлорида аммония. 2. Продолжить записывать температуру через каждую минуту до тех пор, пока вся соль не растворится и не установится изменение температуры, не превышающее 0,010С. После этого записать еще 3-4 показания термометра. |
| 3. Определить изменение температуры Dt калориметрического опыта. | 1. Результаты измерений «предварительного” и “заключительного периодов” калориметрического опыта занести в таблицу (см. приложение к лабораторной работе №1) 2. На основании полученных данных построить график t = f(t). По графику определить Dt. |
| 4. Рассчитать удельную и интегральную теплоты растворения соли. | 5. Используя значение постоянной калориметра из предыдущего занятия, рассчитать удельную теплоту растворения по формуле:  , где К – постоянная калориметра, m – масса растворенной соли, г, а также интегральную теплоту растворения: , где К – постоянная калориметра, m – масса растворенной соли, г, а также интегральную теплоту растворения:  , где М – молярная масса соли. , где М – молярная масса соли. |
| 5. Вычислить погрешность опыта, используя табличное значение интегральной теплоты растворения хлорида аммония. |
З А Н Я Т И Е № 5
Т Е М А: «ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ. ХИМИЧЕСКИЙ ПОТЕНЦИАЛ».
I. МОТИВАЦИЯ ЦЕЛИ: Термодинамическими потенциалами, или характеристическими функциями, называют термодинамические функции, которые содержат в себе всю термодинамическую информацию о системе. Наибольшее значение имеют четыре основных термодинамических потенциала:
1) внутренняя энергия U(S,V),
2) энтальпия H(S,p) = U + pV,
3) энергия Гельмгольца F(T,V) = U - TS,
4) энергия Гиббса G(T,p) = H - TS = F + pV.
В скобках указаны термодинамические параметры, которые получили название естественных переменных для термодинамических потенциалов. Все эти потенциалы имеют размерность энергии и не имеют абсолютного значения, поскольку определены с точностью до постоянной, которая равна внутренней энергии при абсолютном нуле.
Зависимость термодинамических потенциалов от их естественных переменных описывается основным уравнением термодинамики, которое объединяет первое и второе начала. Это уравнение можно записать в четырех эквивалентных формах:
dU = TdS - pdV (5.1)
dH = TdS + Vdp (5.2)
dF = - pdV - SdT (5.3)
dG = Vdp - SdT (5.4)
Эти уравнения записаны в упрощенном виде - только для закрытых систем, в которых совершается только механическая работа.
Зная любой из четырех потенциалов как функцию естественных переменных, можно с помощью основного уравнения термодинамики найти все другие термодинамические функции и параметры системы (см. пример 5-1).
Другой важный смысл термодинамических потенциалов состоит в том, что они позволяют предсказывать направление термодинамических процессов. Так, например, если процесс происходит при постоянных температуре и давлении, то неравенство, выражающее второй закон термодинамики:

эквивалентно неравенству dGp,T  0 (мы учли, что при постоянном давлении
0 (мы учли, что при постоянном давлении  Qp = dH), где знак равенства относится к обратимым процессам, а неравенства - к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.
Qp = dH), где знак равенства относится к обратимым процессам, а неравенства - к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.
В общем случае, любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии:
| Потенциал | Естественные переменные | Условие самопроизвольности | Условия равновесия |
| U | S = const, V = const | dU < 0 | dU = 0, d 2U > 0 |
| H | S = const, p = const | dH < 0 | dH = 0, d 2H > 0 |
| F | T = const, V = const | dF < 0 | dF = 0, d 2F > 0 |
| G | T = const, p = const | dG < 0 | dG = 0, d 2G > 0 |
II. ЦЕЛЬ САМОПОДГОТОВКИ:
1. Изучить термодинамические потенциалы как меру работоспособности системы и как критерии направления процесса.
2. Усвоить соотношения между основными характеристическими функциями системы.
3. Овладеть методом расчета изменения термодинамических потенциалов в химических реакциях.
4. Научиться оценивать возможность, направление и предел протекания химической реакции с позиций химической термодинамики.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ: изменение внутренней энергии, энтропии, энтальпии, способы их расчета, законы термодинамики.
IV. П Л А Н И З У Ч Е Н И Я Т Е М Ы:
1. Максимальная и максимальная полезная работа.
2. Энергия Гиббса. Физический смысл. G как функция состояния.
3. Энергия Гельмгольца. Физический смысл. F как функция состояния.
4. Связь изменения энергии Гиббса или энергии Гельмгольца с работой процесса.
5. Свободная и связанная энергия.
6. Характеристические функции, взаимосвязь между ними.
7. Зависимости энергии Гиббса и энергии Гельмгольца от параметров состояния и состава системы.
8. Объединенное уравнение I и II законов термодинамики. Уравнение Гиббса-Гельмгольца.
9. Термодинамические критерии направления и предела протекания самопроизвольных процессов.
10. Способы расчета изменений энергии Гиббса и энергии Гельмгольца в химических реакциях. Стандартная энергия Гиббса.
11. Полный и частный дифференциал для систем с постоянным и переменным составом.
12. Химический потенциал как фактор интенсивности. Химический потенциал идеального и реального газа. Фугитивность и аддитивность реального газа, методы их определения.
V. ЛИТЕРАТУРА:
1. К.С. Краснов Физическая химия. - М., Высшая школа, 2001, с. 241-251.
2. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 42-50.
3. Киреев В. А. Краткий курс физической химии М. 1978, с.217-237.
4. Стромберг А. Г., Семченко Д.П., Физическая и коллоидная химия, М. 1999, с. 94-107.
5. Лекционный материал.
VI. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Приведите математическое выражение, отражающее соотношение между:
а) энергией Гиббса и энергией Гельмгольца;
б) энергией Гиббса и энтальпией системы;
в) энергией Гельмгольца и внутренней энергией.
2. Какой термодинамический потенциал следует выбрать в качестве критерия протекания самопроизвольного процесса при условии постоянства:
а) температуры и давления;
б) температуры и объема.
3. Перечислите условия, выполнение которых служит критерием термодинамического равновесия в системе:
а) изолированной;
б) находящейся при p = const и T = const;
в) находящейся при V = const и T = const;
в) находящейся при V = const и S = const
в) находящейся при p = const и S = const
4. Какой знак будет иметь величина 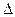 G для процесса перехода жидкого бензола при 273 К в твердое состояние при той же температуре? Температура плавления бензола равна 278,5 К. Какое состояние бензола - жидкое или твердое - является более устойчивым при 273 К?
G для процесса перехода жидкого бензола при 273 К в твердое состояние при той же температуре? Температура плавления бензола равна 278,5 К. Какое состояние бензола - жидкое или твердое - является более устойчивым при 273 К?
5. Для реакции Н2 + Cl2  2HCl изменение энергии Гиббса при 248 К равно - 190,5 кДж. Может ли эта реакция протекать самопроизвольно? Ответ обосновать.
2HCl изменение энергии Гиббса при 248 К равно - 190,5 кДж. Может ли эта реакция протекать самопроизвольно? Ответ обосновать.
6. При работе гальванического элемента Даниэля-Якоби протекает химическая реакция:
Zn + CuCl2  ZnCl2 + Cu
ZnCl2 + Cu
Как изменяется величина 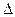 G этой реакции?
G этой реакции?
7. Какие условия необходимо соблюдать, чтобы максимальная работа в системе совершалась за счет убыли энергии Гиббса?
8. В каком соотношении находятся полезная работа, совершенная системой над окружающей средой, и изменение энергии Гельмгольца, если процесс протекает:
а) обратимо;
б) необратимо.
9. Как изменяется энергия Гельмгольца при изотермическом сжатии газа в идеальном состоянии?
10. Напишите уравнение, связывающее изменение энергии Гиббса, температурный коэффициент изменения энергии Гиббса и тепловой эффект процесса при постоянном давлении.
11. Назовите три этапа в расчете изменения изобарного потенциала химической реакции, протекающей в стандартных условиях, если известны значения стандартных теплот образования и стандартных энтропий участников химической реакции.
12. Дайте определение понятию "стандартная энергия Гиббса образования".
13. Приведите уравнение для расчета изменения энергии Гиббса химической реакции по значениям стандартных энергий Гиббса образования всех участников этой реакции.
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 5-1. Внутренняя энергия некоторой системы известна как функция энтропии и объема, U(S,V). Найдите температуру и теплоемкость этой системы.
Решение. Из основного уравнения термодинамики (5.1) следует, что температура - это частная производная внутренней энергии по энтропии:
 .
.
Изохорная теплоемкость определяет скорость изменения энтропии с температурой:
 .
.
Воспользовавшись свойствами частных производных, можно выразить производную энтропии по температуре через вторую производную внутренней энергии:
 .
.
Пример 5-2. Используя основное уравнение термодинамики, найдите зависимость энтальпии от давления при постоянной температуре: а) для произвольной системы; б) для идеального газа.
Решение. а) Если основное уравнение в форме (5.2) поделить на dp при постоянной температуре, получим:
 .
.
Производную энтропии по давлению можно выразить с помощью соотношения Максвелла для энергии Гиббса (5.13):
 .
.
б) Для идеального газа V(T) = nRT / p. Подставляя эту функцию в последнее тождество, получим:
 .
.
Энтальпия идеального газа не зависит от давления.
Пример 5-3. Выразите производные  и
и  через другие термодинамические параметры.
через другие термодинамические параметры.
Решение. Основное уравнение термодинамики (5.1) можно переписать в виде:
 ,
,
представив энтропию как функцию внутренней энергии и объема. Коэффициенты при dU и dV равны соответствующим частным производным:
 .
.
Пример 5-4. Два моль гелия (идеальный газ, мольная теплоемкость Cp = 5/2 R) нагревают от 100 оС до 200 оС при p = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия -  = 131.7 Дж/(моль. К). Можно ли считать этот процесс самопроизвольным?
= 131.7 Дж/(моль. К). Можно ли считать этот процесс самопроизвольным?
Решение. Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре (5.6):
 .
.
Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:
 .
.
Интегрирование этого выражения от 373 К до T дает:
 .
.
Подставляя это выражение в интеграл от энтропии, находим:

Процесс нагревания не обязан быть самопроизвольным, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при T = const и p = const.
Ответ.  G = -26850 Дж.
G = -26850 Дж.
Пример 5-5. Рассчитайте изменение энергии Гиббса в реакции
CO + 1/2O2 = CO2
при температуре 500 K и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.
Решение. Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
| Вещество | Энтальпия образования  , кДж/моль , кДж/моль | Энтропия  , Дж/(моль.К) , Дж/(моль.К) | Теплоемкость  , Дж/(моль.К) , Дж/(моль.К) |
| CO | -110.5 | 197.6 | 29.14 |
| O2 | 205.0 | 29.40 | |
| CO2 | -393.5 | 213.7 | 34.57 |
| Реакция | 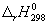 , кДж/моль , кДж/моль |  , Дж/(моль. К) , Дж/(моль. К) |   , Дж/(моль.К) , Дж/(моль.К) |
| CO + 1/2O2 = CO2 | -283.0 | -86.4 | -9.27 |
Примем, что  Cp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
Cp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
 f = f(CO2) - f(CO) - f(O2).
f = f(CO2) - f(CO) - f(O2).
Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме:

Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле:

Стандартное изменение энергии Гиббса при 500 К:

Для расчета изменения энергии Гиббса при парциальных давлениях 3 атм необходимо проинтегрировать формулу

и использовать условие идеальности газов (  V =
V =  n RT / p,
n RT / p,  n - изменение числа молей газов в реакции):
n - изменение числа молей газов в реакции):

Эта реакция может протекать самопроизвольно при данных условиях.
Ответ.  G = -242.5 кДж/моль.
G = -242.5 кДж/моль.
5-1. Выразите внутреннюю энергию как функцию переменных G, T, p.
5-2. Используя основное уравнение термодинамики, найдите зависимость внутренней энергии от объема при постоянной температуре: а) для произвольной системы; б) для идеального газа.
5-3. Известно, что внутренняя энергия некоторого вещества не зависит от его объема. Как зависит давление вещества от температуры? Ответ обоснуйте.
5-4. Напишите выражение для бесконечно малого изменения энтропии как функции внутренней энергии и объема. Найдите частные производные энтропии по этим переменным и составьте соответствующее уравнение Максвелла.
5-5. Для некоторого вещества известно уравнение состояния p(V, T). Как изменяется теплоемкость Cv с изменением объема? Решите задачу: а) в общем виде; б) для какого-либо конкретного уравнения состояния (кроме идеального газа).
5-6. Нарисуйте график зависимости энергии Гиббса индивидуального вещества от температуры в интервале от 0 до T > Tкип.
5-7. Вычислите изменение H, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0.5 м3 до 1.35 м3 0.7 молей азота (CV = 5/2 R). Энтропия газа в исходном состоянии равна 150 Дж/(моль. К), газ можно считать идеальным.
5-8. Вычислите изменение энергии Гиббса при сжатии от 1 атм до 3 атм при 298 К: а) одного моля жидкой воды; б) одного моля водяного пара (идеальный газ).
5-9. Изменение энергии Гиббса в результате испарения воды при 95 оС и 1 атм равно 546 Дж/моль. Рассчитайте энтропию паров воды при 100 оС, если энтропия жидкой воды равна 87.0 Дж/(моль. К). При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 95 оС?
5-10. Вычислите стандартную энергию Гиббса образования (  ) жидкой и газообразной воды, если известны следующие данные:
) жидкой и газообразной воды, если известны следующие данные:  (H2O(г)) = -241.8 кДж/моль,
(H2O(г)) = -241.8 кДж/моль,  (H2O(ж)) = -285.6 кДж/моль,
(H2O(ж)) = -285.6 кДж/моль,  (H2) = 130.6 Дж/(моль. К),
(H2) = 130.6 Дж/(моль. К),  (O2) = 205.0 Дж/(моль. К),
(O2) = 205.0 Дж/(моль. К),  (H2O(г)) = 188.5 Дж/(моль. К),
(H2O(г)) = 188.5 Дж/(моль. К),  (H2O(ж)) = 69.8 Дж/(моль. К).
(H2O(ж)) = 69.8 Дж/(моль. К).
5-11.Рассчитайте  Go при 25 оС для химической реакции:
Go при 25 оС для химической реакции:
4HCl(г) + O2(г) = 2Cl2(г) + 2H2O(ж).
Стандартные значения энтальпии образования и абсолютной энтропии при 25 оС равны:  fHo(HСl) = -22.1 ккал/моль,
fHo(HСl) = -22.1 ккал/моль,  fHo(H2O(ж)) = -68.3 ккал/моль; So(HCl) = 44.6 кал/(моль. K), So(O2) = 49.0 кал/(моль. K), So(Сl2) = 53.3 кал/(моль. K), So(H2O(ж)) = 16.7 кал/(моль. K).
fHo(H2O(ж)) = -68.3 ккал/моль; So(HCl) = 44.6 кал/(моль. K), So(O2) = 49.0 кал/(моль. K), So(Сl2) = 53.3 кал/(моль. K), So(H2O(ж)) = 16.7 кал/(моль. K).
5-12. Рассчитайте  Go при 25 оС для химической реакции:
Go при 25 оС для химической реакции:
CO2(г) + 4H2(г) = CH4(г) + 2H2O(ж).
Стандартные значения энтальпии образования и абсолютной энтропии при 25 оС равны:  fHo(СO2) = -94.1 ккал/моль,
fHo(СO2) = -94.1 ккал/моль,  fHo(СH4) = -17.9 ккал/моль,
fHo(СH4) = -17.9 ккал/моль,  fHo(H2O(ж)) = -68.3 ккал/моль; So(СO2) = 51.1 кал/(моль. K), So(H2) = 31.2 кал/(моль. K), So(СH4) = 44.5 кал/(моль. K), So(H2O(ж)) = 16.7 кал/(моль. K).
fHo(H2O(ж)) = -68.3 ккал/моль; So(СO2) = 51.1 кал/(моль. K), So(H2) = 31.2 кал/(моль. K), So(СH4) = 44.5 кал/(моль. K), So(H2O(ж)) = 16.7 кал/(моль. K).
5-13. Рассчитайте стандартные энергии Гиббса и Гельмгольца  Go и
Go и  Fo при 300 оС для химической реакции:
Fo при 300 оС для химической реакции:
CO(г) + 3H2(г) = CH4(г) + H2O(г).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-14. Найдите энергию Гиббса образования NH3 при температурах 298 и 400 K, если известны следующие данные:  (NH3) = -46.2 кДж/моль,
(NH3) = -46.2 кДж/моль,
| Вещество | N2 | H2 | NH3 |
| Cp,298, Дж/(моль. К) | 29.1 | 28.8 | 35.7 |
 , Дж/(моль. К) , Дж/(моль. К) | 191.5 | 130.6 | 192.5 |
Считать, что теплоемкости в указанном интервале температур постоянны.
5-15. Рассчитайте стандартные энергии Гиббса и Гельмгольца  Go и
Go и  Fo при 60 оС для химической реакции:
Fo при 60 оС для химической реакции:
CH3COOH(ж) + 2H2(г) = C2H5OH(ж) + H2O(ж).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-16. Рассчитайте стандартные энергии Гиббса и Гельмгольца  Go и
Go и  Fo при 700 оС для химической реакции:
Fo при 700 оС для химической реакции:
CaCO3(тв) = CaO(тв) + CO2(г).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
5. Выполнение лабораторной работы “Определение теплоты нейтрализации сильного основания сильной кислотой”.
Лабораторная работа №3
“Определение теплоты нейтрализации сильного основания сильной кислотой”
Теплотой нейтрализации называют количество теплоты, выделяющееся при взаимодействии 1 моль эквивалента кислоты и 1 моль эквивалента щелочи.
Нейтрализация сильного основания сильной кислотой сопровождается протеканием химической реакции, уравнение которой в ионном виде имеет вид:
Н+ + ОН-® Н2О
или
Н3О+ + ОН- ® 2 Н2О
| ВИД ДЕЙСТВИЯ | СПОСОБ ДЕЙСТВИЯ |
| 1. Собрать калориметр и провести “предварительный период” калориметрического опыта | 1. В калориметрический стакан емкостью 100 мл внести 40 мл 0,2 Н раствора NaОН. В стакан поместить мешалку и термометр. Закрыть калориметр крышкой. 2. Медленно размешивая мешалкой содержимое стакана, сделать 11 отсчетов температуры с интервалом 30 с. 3. Полученные данные записать в таблицу. |
| 2. Провести «главный» и «заключительный периоды» калориметрического опыта | 1. После 11 отсчета температуры быстро при постоянном перемешивании внести в калориметрический стакан 10 мл 1н раствора НСl. 2. Произвести отсчет температуры. «Главный период» продолжается 2-3 мин. Затем провести 10 отсчетов температуры «заключительного периода». |
| 3. Определить изменение температуры Dt калориметрического опыта | 1. Построить график зависимости температуры от времени опыта (смотреть 3 этап работы №1). |
| 4. Рассчитать количество теплоты, выделившейся при нейтрализации сильного основания (NaОН) сильной кислотой (НСl). | 1. Рассчитать постоянную калориметра по формуле : K = S ci mi , приняв теплоемкости растворов электролитов равными теплоемкости воды. 2. Количество выделенной теплоты рассчитать по уравнению: DH = - K × Dt (кДж). |
| 5. Рассчитать теплоту нейтрализации DHнейтр | 1. Рассчитать количество вещества вступившего в реакцию эквивалента NaОН, n (NaОН) (кислота НСl взята в избытке). 2. DHнейтр рассчитать по уравнению:  |
Таблица
| Время от начала опыта, мин. | Предварительный период | Главный период | Заключительный период | ||||||
| … | |||||||||
| t0C |
Постоянную калориметра приближенно рассчитать по соотношению:
K = Cуд стекла × mстакана + Cуд NaOH × VNaOH × rNaOH + Cуд HCl ×VHCl × rHCl +
+ Cоб.рт. резерв. т-ра × Vт-ра + Смешалки
Дополнительные данные к работе:
| ВЕЩЕСТВО | УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ, Дж/г К |
| Стекло Вода Разбавленные растворы электролитов Ртуть, стекло | 0,791 4,184 4,184 1,925 (Дж/см3 К) |
Плотность растворов NaОН и НСl принять равной плотности воды и равной 1 г/см3
mстакана =
Vт-ра =
Смешалки =
З А Н Я Т И Е № 6
ТЕМА:« ТЕРМОДИНАМИКА ХИМИЧЕСКИХ РАВНОВЕСИЙ»
I. МОТИВАЦИЯ ЦЕЛИ: Теория химического равновесия имеет большое значение для интенсификации химического и фармацевтического производства, так как дает возможность найти оптимальные условия проведения того или иного химического процесса, при котором выход продуктов данной реакции становится достаточно большим.
Нужно, однако, иметь в виду, что реальные оптимальные условия проведения реакции на производстве определяются не только желанием достигнуть возможно большего выхода готового продукта, но в значительной степени зависят от скорости протекания данной реакции при различных температурах.
II. ЦЕЛЬ САМОПОДГОТОВКИ: понимать особенности состояния равновесия, знать, что такое “термодинамическое равновесие”, критерии термодинамического равновесия, возможности применения теории равновесий для описания состояния систем и возможностей протекания процессов, усвоить уравнения изобары и изохоры.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ: законы термодинамики, критерии термодинамического течения процесса, виды термодинамических систем и их связь со средой, уравнение Вант-Гоффа, уравнение Гиббса-Гелъмголъца, представления о константе равновесия.
IV. ПЛАН ИЗУЧЕНИЯ МАТЕРИАЛА ТЕМЫ:
1. Термодинамика химического равновесия.
2. Закон действующих масс.
3. Термодинамическая константа равновесия, практические константы равновесия Kp и KC. Стандартное сродство и реакционная способность
4. Особенности выражения константы равновесия для гетерогенной реакции.
5. Зависимость константы равновесия от температуры.
6. Вывод уравнения изотермы химической реакции.
7. Вывод уравнения изобары (изохоры) химической реакции.
8. Интегрирование уравнения изобары без учета и с учетом температурной зависимости теплового эффекта.
9. Вычисление константы равновесия: приближенные и точные способы.
10. Применение стандартных термодинамических величин при расчете константы равновесия. Уравнение Шварцмана-Темкина.
V. ЛИТЕРАТУРА:
1. К.С. Краснов Физическая химия. - М., Высшая школа, 2001, с. 265-272, 282-288.
2. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 42-50.
3. Стромберг А.Г., Семченко Д.П. Физическая химия М., 1999, с. 108-128.
VI. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ.
1. Что такое равновесное состояние вещества?
2. В чем особенности термодинамического равновесия?
3. Константа равновесия. Какие факторы влияют на константу термодинамического равновесия?
4. Возможны ли процессы химических превращений в состоянии термодинамического равновесия?
5. Приведите уравнение, связывающее константы термодинамического и концентрационного равновесия.
6. Приведите выражения законов термодинамики для равновесного состояния системы.
7. Приведите значения изменения изобарно-изотермического потенциала в условиях термодинамического равновесия.
8. Приведите значения изохорно-изотермического потенциала в состоянии равновесии в условиях постоянства температуры и давления.
9. Какое уравнение позволяет связать изменение энергии Гиббса с константой равновесия?
10. В чем особенность изменения состояния энтропии для различных случаев химических превращений?
11. Приведите условия состояния термодинамического равновесия для эндотермических реакции с возрастанием энтропии.
12. Какие ограничения накладываются на систему, если ее равновесность констатирована по критерию DН?
13. Запишите математическое выражение для фазового равновесия в условиях постоянства объема.
14. Чему будет равен химический потенциал в состоянии термодинамического равновесия при Т и Р = const?
15. Запишите значения изменения термодинамических функций в условиях равновесного состояния после течения самопроизвольной химической реакции с возрастанием энтропии.
16. Запишите уравнения изобары и изохоры в дифференциальной форме.
17. Что такое температурный коэффициент константы химического равновесия
18. Какие значения должен иметь температурный коэффициент если реакция сопровождается выделением энергии?
19. Роль теплового эффекта химической реакции для описания характера течения процесса
20. График зависимости константы химического равновесия химической реакции от температуры.
21. Запишите интегральную форму уравнений изохоры и изобары.
22. Принцип смещения равновесия Ле Шателье-Брауна.
23. Приведите график зависимости константы равновесия от температуры для экзотермических процессов.
24. Приведите график зависимости константы равновесия от температуры для эндотермических процессов.
25. Покажите возможность объединения уравнения изобары и уравнения Кирхгофа.
26. В чем сущность метода вычисления теплового эффекта химической реакции по второму закону термодинамики?
27. Приведите зависимость логарифма константы равновесия реакции от температуры.
28. Что обозначает тангенс угла наклона на этом графике?
29. Что обозначает отрезок, отсекаемый прямой на оси ординат?
30. Зависимость Кp некоторой реакции от обратной температуры представляет прямую линию. Экзотермическая или эндотермическая это реакция?
31. Зависимость Кр от 1/T представлена возрастающей прямой линией. Какое заключение можно сделать о характере температурной зависимости в данном интервале температур?
32. Для некоторой эндотермической реакции тепловой эффект с ростом температуры увеличивается. Каков общий вид графической зависимости Кр от 1/Т для этой реакции?
33. В каких условиях проведения эксперимента имеет смысл учитывать температурную зависимость констант равновесия.
34. Имеются экспериментальные данные о значениях константы равновесия при разных температурах. Как рассчитать истинный тепловой эффект реакции при заданной температуре?
Нарисовать кривую зависимости Кр от 1/Т для экзотермической реакции и показать на ней нахождение постоянных величин.
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 9-1. Рассчитать константу равновесия для реакции
CO(г) + 2H2(г) = CH3OH(г)
при 500 K.  fGo для CO(г) и CH3OH(г) при 500 К равны –155.41 кДж. моль–1 и –134.20 кДж. моль–1 соответственно.
fGo для CO(г) и CH3OH(г) при 500 К равны –155.41 кДж. моль–1 и –134.20 кДж. моль–1 соответственно.
Решение.  Go реакции:
Go реакции:
 rGo =
rGo =  fGo (CH3OH) –
fGo (CH3OH) –  fGo (CO) = –134.20 – (–155.41) = 21.21 кДж. моль–1.
fGo (CO) = –134.20 – (–155.41) = 21.21 кДж. моль–1.
 = 6.09
= 6.09  10–3.
10–3.
Пример 9-2. Константа равновесия реакции
N2(г) + 3H2(г) = 2NH3(г)
равна KP = 1.64  10–4 при 400o C. Какое общее давление необходимо приложить к эквимолярной смеси N2 и H2, чтобы 10% N2 превратилось в NH3? Газы считать идеальными.
10–4 при 400o C. Какое общее давление необходимо приложить к эквимолярной смеси N2 и H2, чтобы 10% N2 превратилось в NH3? Газы считать идеальными.
Решение. Пусть прореагировало  моль N2. Тогда
моль N2. Тогда
| N2(г) | + | 3H2(г) | = | 2NH3(г) | |
| Исходное количество | |||||
| Равновесное количество | 1–  | 1–3  | 2  (Всего: 2–2 (Всего: 2–2  ) ) | ||
| Равновесная мольная доля: |  |  |  |
Следовательно, KX =  и KP = KX. P–2 =
и KP = KX. P–2 =  .
.
Подставляя  = 0.1 в полученную формулу, имеем
= 0.1 в полученную формулу, имеем
1.64  10–4 =
10–4 =  , откуда P = 51.2 атм.
, откуда P = 51.2 атм.
Пример 9-3. Константа равновесия реакции
CO(г) + 2H2(г) = CH3OH(г)
при 500 K равна KP = 6.09  10–3. Реакционная смесь, состоящая из 1 моль CO, 2 моль H2 и 1 моль инертного газа (N2) нагрета до 500 K и общего давления 100 атм. Рассчитать состав равновесной смеси.
10–3. Реакционная смесь, состоящая из 1 моль CO, 2 моль H2 и 1 моль инертного газа (N2) нагрета до 500 K и общего давления 100 атм. Рассчитать состав равновесной смеси.
Решение. Пусть прореагировало  моль CO. Тогда
моль CO. Тогда
| CO(г) | + | 2H2(г) | = | CH3OH(г) | |
| Исходное количество: | |||||
| Равновесное количество: | 1–  | 2–2  |  | ||
| Всего в равновесной смеси: | 3–2  моль компонентов + 1 моль N2 = 4–2 моль компонентов + 1 моль N2 = 4–2  моль моль | ||||
| Равновесная мольная доля |  |  |  |
Следовательно, KX =  и KP = KX. P–2 =
и KP = KX. P–2 =  .
.
Таким образом, 6.09  10–3 =
10–3 =  .
.
Решая это уравнение, получаем  = 0.732. Соответственно, мольные доли веществ в равновесной смеси равны:
= 0.732. Соответственно, мольные доли веществ в равновесной смеси равны:  = 0.288,
= 0.288,  = 0.106,
= 0.106,  = 0.212 и
= 0.212 и  = 0.394.
= 0.394.
Пример 9-4. Для реакции
N2(г) + 3H2(г) = 2NH3(г)
при 298 К KP = 6.0  105, а
105, а  fHo (NH3) = –46.1 кДж. моль–1. Оценить значение константы равновесия при 500 К.
fHo (NH3) = –46.1 кДж. моль–1. Оценить значение константы равновесия при 500 К.
Решение. Стандартная мольная энтальпия реакции равна
 rHo = 2
rHo = 2  fHo (NH3) = –92.2 кДж. моль–1. Тогда:
fHo (NH3) = –92.2 кДж. моль–1. Тогда:
 = ln (6.0
= ln (6.0  105) +
105) +  = –1.73, откуда K2 = 0.18.
= –1.73, откуда K2 = 0.18.
Отметим, что константа равновесия экзотермической реакции уменьшается с ростом температуры, что соответствует принципу Ле - Шателье.
Пример 9-5.
Определите направление реакции
2C2H5OH = C4H6 + 2H2O + H2
при Т = 600 К и стандартных условиях.
Решение. Для систем, находящихся при постоянной температуре и давлении, критерием, определяющим возможность, направление и предел протекания химических реакций, является изменение свободной энергии Гиббса при стандартных условиях. Если изменение свободной энергии Гиббса в ходе реакции имеет отрицательный знак, то процесс самопроизвольно протекает в прямом направлении, т. е. слева направо. При (DrG°)pT>0 направление самопроизвольного процесса будет обратным, а при (DrG°)pT = 0 система будет находиться в состоянии равновесия. Из различных методов расчета DrG° наибольшее применение получил метод Шварцмана - Темкина, согласно которому
DrG°T = DrН°298 - ТDrS°298 – T(DaM0 + DbM1 + DcM2),
где DrН°298 и DrS°298 - тепловой эффект и изменение энтропии при Т = 298 К;
Da, Db, Dc - разность коэффициентов степенных рядов зависимости от температуры;
М1, М2, М3 - коэффициенты уравнения Шварцмана - Темкина, величина которых зависит только от температуры реакции и не зависит от ее природы.
Рассчитываем DrН°298, DrS°298, Da, Db, Dc реакции (см. примеры решения задач по расчету тепловых эффектов):
DrН°298 = 2(— 241,84) + 111,9— 2(— 235,3) =98820 Дж,
DrS°298 = 2 ´188,74+ 130,6+278,7— 2 ´ 282= 222,78 Дж/ К,
Da = 2 .30,0+27,28 - 2,96 – 2 ´ 19,07=46,18 Дж/К,
Db = (2 ´ 10,7 1+3,26+340,08 – 2 ´ 212,7) ´ 10-3 = - 60,64´10-3 Дж/К2,
Dc =(2´l08,6 - 223,7) ´ 10-6= - 6,5 ´ 10-6 Дж/К3.
Из таблицы выписываем значения коэффициентов уравнения Шварцмана — Темкина при Т = 600 К:
