Проверка гипотезы о равенстве дисперсий

При обработке экспериментальных данных часто требуется выяснить во­прос об однородности выборочных дисперсий т.е. их равенстве дисперсии ге­неральной совокупности.

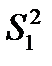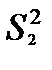Пусть для двух независимых выборок из нормальной генеральной совокуп­ности с объемами m₁ и m₂ вычислены оценки и . Требуется проверить нулевую гипотезу (Н₀) 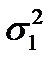= 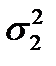относительно альтерна­тивной гипотезы (Н₁) 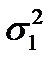> 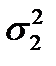. Проверка проводится при помощи критерия Фишера F.

Наблюдаемое значение критерия

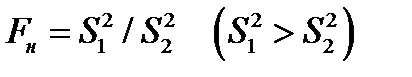(3.17)

сравнивается с критическим F_к, которое определяется из табл. П.7 для вы­бранных доверительной вероятности и m₁ и m₂. Если F_н<F_к, то выборочные данные не противоречат нулевой гипотезе.

При анализе выборочных данных могут выдвигаться гипотезы об однород­ности дисперсий в нескольких выборках. В этом случае можно использовать критерий Кохрена. Наблюдаемое значение критерия G_н определяется по фор­муле

(3.18)

где S²_imax — максимальная оценка дисперсии среди п сравниваемых дисперсий (все п выборок имеют одинаковый объем т).

Критическое значение критерия определяется из табл. П.8 в зависимости от принятых доверительной вероятности Р, объема выборок т и их числа п.

Пример 3.4. Проверить гипотезу о равенстве дисперсий в примере 3.3.

Решение. По формуле (3.17) определяем наблюдаемое значение крите­рия Фишера F_н= 4,76/3,8 = 1,25. Из табл. П.7 для Р = 0,95, m₁ = m₂ =20 находим F_к = 2,16, а для m₁ = m₂ = 30 - F_к = 1,84. Искомое значение F_к для m₁ = m₂ = 25 находим линейной интерполяцией: F_к = (1,84 + 2,16)/2=2.

Так как F_н<F_к (1,25 < 2), нулевая гипотеза о равенстве дисперсий принимается.

Пример 3.5. С четырех автоматов, настроенных на обработку одних и тех же деталей, взято по одной текущей выборке объемом т = 10. Оценки диспер­сий их размеров имели следующие значения: 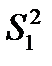= 106 мкм²; 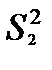= 294; =216; 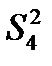= 410 мкм². Требуется определить, одинакова ли точность автоматов, т.е. можно ли принять гипотезу об однородности дисперсий.

Решение. Согласно (3.18),

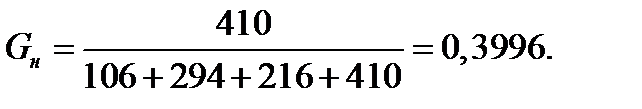
По табл. П.8 для Р = 0,95, m=10 и n = 4 находим G_к= 0,502. Поскольку G_н<G_к (0,3996<0,502), то можно считать точность автоматов практически одинаковой.

3.3.5. Проверка случайности и независимости результатов
измерений в выборке

До статистической обработки результатов измерения отклика необходимо убедиться в том, что они являются стохастически независимыми. Альтернатив­ной гипотезой может быть предположение о наличии монотонного или циклического смещения (дрейфа) значения отклика, вызванного неконтролируемым фактором. Подобный случай может иметь место при анализе размеров дета­лей, обрабатываемых на настроенном станке, когда вследствие изнашивания инструмента или нагрева станка центр группирования размеров постепенно сме­щается при неизменной стандартной погрешности. Наиболее мощным крите­рием проверки нулевой гипотезы будет критерий последовательных разно­стей τ.

Наблюдаемое значение критерия

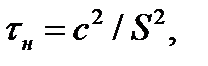
где

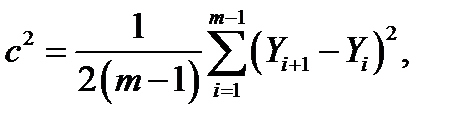
m — объем выборки; i — порядковый номер измерения отклика в выборке; S² — оценка дисперсии, вычисляемая по формулам (3.7), (3.9) или (3.10).

Критическое значение τ_к определяется из табл. П.9 в зависимости от при­нятой доверительной вероятности Р и объема выборки т. Если τ_н<τ_к, то гипо­теза о независимости и случайности измерений в выборке отвергается.

Пример 3.6. По результатам измерения деталей, обработанных на токарно­револьверном автомате, необходимо проверить наличие или от­сутствие дрейфа размеров. Объем выборки m = 40.

Решение.

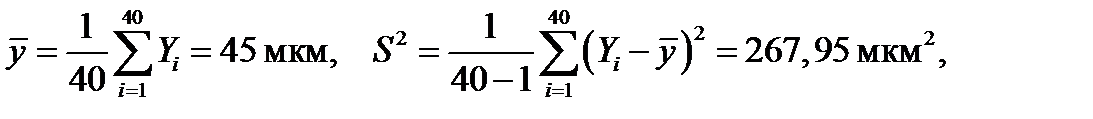
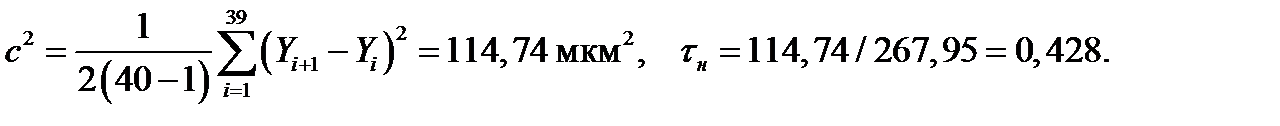
По табл. П.9 для m = 40 и Р = 0,95 получаем τ_к= 0,742. Так как τ_н<τ_к (0,428<0,742), гипотезу об отсутствии дрейфа следует отклонить. Следователь­но, размер обрабатываемых деталей зависит от неучтенного фактора, вызвав­шего циклическое смещение центра группирования размеров.