Теорема Гаусса для электрического поля в среде. Вектор электрического смещения и его связь с вектором напряженности.
Основной прикладной задачей электростатики является расчет электрических полей, создаваемых заряженными телами.
В частном случае такой расчет можно произвести с помощью закона Кулона и принципа суперпозиции электрического поля. Но в ряде случаев эта задача сильно усложняется. Например: 1) большое число точечных зарядов, создающих электростатическое поле или распределенный заряд на теле сложной формы; 2) электрическое поле создается в среде с неоднородным диэлектриком.
Во втором случае вектор напряженности электрического поля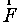 
зависит от диэлектрической проницаемости e среды, в которой создано поле
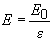, (2.1)
 | где 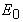 – напряженность электрического поля в вакууме; e – относительная диэлектрическая проницаемость среды. |
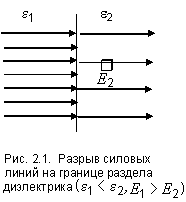
В связи с этим при переходе через границу раздела сред напряженность электрического поля и характеризующая его густота силовых линий будут скачкообразно меняться (рис. 2.1). Картина будет еще сложнее в случае неоднородного электрического поля и диэлектрика произвольной формы.
Для облегчения расчета электрических полей в неоднородных диэлектриках вводится понятие вектора электрического смещения иливектора электрической индукции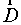 
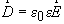, (2.2)
где e0 – электрическая постоянная; e – относительная диэлектрическая проницаемость среды;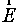 
– вектор напряженности электрического поля.
Направление вектора электрического смещения 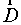совпадает с направлением вектора напряженности 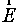. Согласно определению вектора электрического смещения 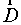и выражения (2.2) можно записать
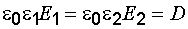. (2.3)
Из выражения (2.3) видно, что вектор электрического смещения не зависит от среды, в которой создается электрическое поле, и определяется только зарядами, создающими это поле. Графически такое поле представлено на рис. 2.2. Как видно из рисунка, силовые линии вектора электрического смещения непрерывны на границе раздела диэлектрика.
Число линий электрического смещения, пресекающих единичную поверхность, расположенную перпендикулярно линиям смещения, равно величине электрического смещения.
Рассмотрим в однородном электрическом поле плоскую поверхность S, ориентация в пространстве этой поверхности определяется направлением нормали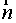 
(рис. 2.3).
 |  |
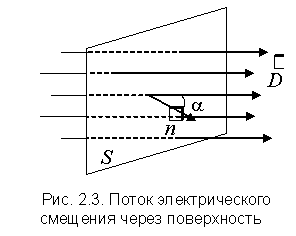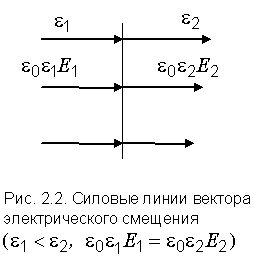Линии электрического смещения составляют угол a с направлением нормали. Величину
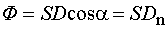(2.4)
называют потоком вектора электрического смещениячерез данную поверхность. Через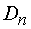 
обозначена проекция вектора 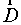на направление нормали 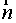. Так как число линий, приходящихся на единицу площади поверхности электрического смещения, равно 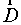, то можно сказать, что поток вектора электрического смещения через данную поверхность равен числу линий электрического смещения, проходящих через эту поверхность.
Если поле неоднородно или поверхность, через которую определяется поток, не является плоской, то эту поверхность можно разбить на бесконечно малые элементы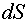 
. Тогда для любого поля поток смещения через этот элемент поверхности
.
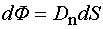Полный поток смещения через поверхность S определится суммированием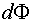 
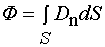. (2.5)
Отметим, что поток смещения, определяющий число проходящих линий смещения, есть величина скалярная.
Остроградским и Гауссом была установлена связь полного потока через замкнутую поверхность с зарядами, охваченными ею.
Эта связь устанавливается теоремой Остроградского–Гаусса: поток электрического смещения через любую замкнутую поверхность равен алгебраической сумме всех зарядов, расположенных внутри поверхности
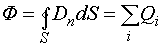. (2.6)
Если в рассматриваемом пространстве имеется распределенный в объеме заряд с объемной плотностью r = r(x,y,z), то теорему Остроградского–Гаусса можно записать в дифференциальной форме
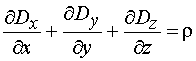. (2.7)
Выражение (2.7) носит название уравнения Пуассона.