Распределение ионов в растворах электролитов. Теория сильных электролитов

Чтобы описать ион-ионное взаимодействие в растворах электролитов необходимо знать распределение ионов в растворе и природу сил действующих между ними.

Как показали исследования оптических и спектральных свойств в растворах сильных электролитов практически не обнаруживается существование недиссоциированных молекул, в растворах же слабых электролитов недиссоциированные молекулы присутствуют.

По современным представлениям процесс диссоциации слабых электролитов является обратным процессом, т.е. теория электролитической диссоциации рассматривает процесс диссоциации молекулы на ионы и образование ее из ионов.

МА 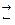М⁺ + А^–

Теория же сильных электролитов должна учитывать совокупность взаимодействия каждого данного иона со всеми остальными окружающими его ионами того и другого знака.

Так как одноименно заряженные ионы взаимно отталкиваются, а разноименно заряженные – взаимно притягиваются, то каждый ион в растворе окружается ближе к нему расположенными ионами противоположного знака, в то время как одноименно заряженные ионы располагаются в среднем дальше от него (вследствие этого притяжение преобладает над отталкиванием). Таким образом, каждый ион окружается как бы роем ионов (ионной атмосферой).

При этом каждый из ионов, составляющих данную атмосферу, очевидно, сам в свою очередь является центром ионной атмосферы, окружающей его.

В результате проявляется тенденция к более или менее закономерному размещению ионов по всему объему раствора.

Размещение это можно представить аналогичным размещению ионов в соответствующих ионных кристаллах, но отмечается большим расстоянием между ионами и присутствием растворителя, которое осложняется электростатическое взаимодействие ионов ион-дипольным взаимодействием. Кроме того, в растворах сильных электролитов при увеличении концентрации может происходить ассоциация ионов, когда противоположно заряженные ионы сближаются и влияние их друг на друга усиливается, но, не на столько сильно, как при типичном образовании молекул.

Все это при диссоциации электролита влияет аналогично тому, как если бы уменьшилась степень диссоциации.

При рассмотрении термодинамических свойств растворов электролитов широко используется понятие ионной силы (Y) раствора, которую можно рассматривать как меру интерактивности электрического поля, создаваемого ионами в растворе.

Величина ионной силы существенно влияет на термодинамические свойства электролита и определяется соотношением

Y 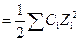(1.13)

Где С_i концентрация данного вида иона, а Z – его заряд.

А всю совокупность взаимодействий, возникающих в растворах электролитов, можно формально описать, используя вместо аналитической концентрации кажущуюся концентрацию – активность электролита или активность его ионов, т.е. ту эффективную концентрацию которая является реально действующей в химических процессах. Активность электролита обозначают буквой «а»и она равна произведению аналитической концентрации на коэффициент активности.

Поскольку концентрацию можно выражать в моляльности (С_m – количество молей в 1 л раствора), и в мольных долях (N₂ – отношение количества числа молей растворенного вещества к общему числу молей в объеме раствора), то имеются три шкалы активностей и коэффициентов активности.

Но при описании растворов электролитов концентрацию чаще всего выражают в моляльности и связь между активностью а и коэффициентом активности γ_m и моляльной концентрации С_m определяется формулой

а = γ_m * С_m (1.14)

А физический смысл коэффициента активности интерпретировать можно как работу перехода из реального состояния в идеальное, т.е. он характеризует отклонение свойств рассматриваемой реальной системы от свойств идеальных систем, или точнее от свойств, которыми обладала бы система, состоящая из данных компонентов, если бы она принадлежала к идеальным системам.

Общая активность характеризует электролит в целом и зависит от активностей отдельных ионов (а+, а-) и может быть представлена как их произведение.

В электролите концентрацию каждого вида иона можно рассчитать по формуле:

С_иона = С_эл * α * n (1.17)

Где n – число ионов данного вида на которое распадается молекула, α – степень диссоциации.

А их активности при условии полной диссоциации к моляльной концентрации определяются соотношениями

а+ = С+ * γ+= С_эл * n+ * γ+ (1.16)

а- = С- * γ-= С_эл * n- * γ- (1.17)

При рассмотрении бинарного электролита (АВ) диссоциирующего АВ = А⁺ + В^–

а_А⁺ = С_А⁺ * γ⁺= С_эл * γ⁺ (1.18)

а_В- = С_В- * γ-= С_эл * γ- (1.19)

А активность электролита можно представить как произведение активности ионов:

а_АВ = а_А⁺ * а_В^- (1.20)

Заменив активности ионов их значениями, получим

а_АВ = С_А⁺ * С_В- * γ⁺ * γ⁺= С_эл² * γ⁺ * γ^- (1.21)

Для более сложного электролита (А_nВ_m) диссоциирующего А_nВ_m = nА^m+ + mВ^n-

а _АnВm = аⁿ_Аm+ * а^m_Вn- = С^n+m * nⁿ * m^m * γ₊ⁿ * γ-^m (1.22)

Поскольку иметь дело с одним сортом ионов в растворе эквивалента невозможно, но также невозможно и раздельное определение активности ионов и коэффициентов, было введено понятие о средних величинах: активности и коэффициенте активности (а±) и (γ±).

Для электролита АВ:

γ± = 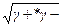или γ±² = γ+ * γ- (1.23)

а± = 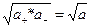или а±² = а₊ * а- = а (1.24)

Для электролита А_nВ_m:

γ± = 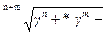(1.25)

а± = 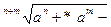(1.26)

Средний коэффициент активности оценить можно по эмпирическому правилу ионной силы. По этому правилу средний коэффициент активности при данной ионной силе раствора не зависит от природы и концентрации, но зависит от числа ионной, на которое распадается электролит и от зарядов ионов.

lg γ ± = - h * Y (1.27)

причем h = 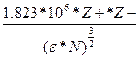(1.28)

где ε – диэлектрическая проницаемость – величина показывающая, во сколько раз сила взаимодействия двух зарядов в данной среде меньше, чем в вакууме. Если Т = 298 К, а ε = ε_воды = 78,3, то

lg γ ± = - 0,509 * Z+ * Z- * 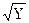(1.29)

Это уравнение называется уравнением первого приближения теории Дебая-Гюккеля. Этим уравнением также обосновывается эмпирически установленное ранее правило ионной силы, согласно которому:

Во всех разбавленных растворах сильных электролитов при одной и той же ионной силе средние коэффициенты активности при одной и той же зарядности ионов одинаковы.

Примеры решения задач.

Пример № 1.

Рассчитать ионную силу 0,001 моляльного водного раствора ВаСl₂.

Данная соль диссоциирует по уравнению ВаСl₂ 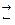Ва²⁺ + 2Сl^-,

причем С_Ва²⁺ = 2С_Сl-, а ионная сила рассчитывается по уравнению

Y 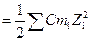и будет равна Y 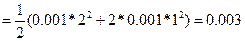(Y= 3Cm)

Пример № 2

Определите активность и среднюю активность сульфата цинка в 0,001 моляльном водном растворе.

1. Сульфат цинка диссоциирует по уравнению ZnSO₄ = Zn²⁺ + SO₄^2-,

причем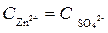

Ионную силу рассчитать по уравнению Y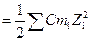

Y 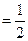(0,001 * 2² + 0,001 * 2²) = 0,004

2. По уравнению Дебая-Гюккеля рассчитать средний коэффициент активности

lg γ ± = - 0,509 * Z+ * Z- *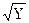

lg γ ± = - 0,509 * 2 * 2 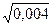= - 0,1287

lg γ ± = 0,7435

3. Рассчитать активность используя формулу.

а = а⁺ * а^-

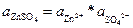
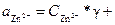
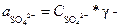
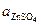= 0,001 * γ+ * 0,001 * γ- = 0,001²* γ±² = 5,5 *10^-7

а± = 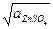= 7,43 * 10^-4