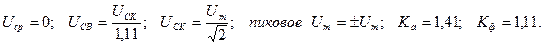Основные значения измеряемых напряжений и токов

Тема 4. Измерение напряжений и токов

Основные значения измеряемых напряжений и токов

На практике часто измеряют напряжения, несколько реже - токи. Это объясняется тем, что для измерения тока измеряемую цепь необходимо разрывать, что не всегда возможно или желательно. Измеряемые электрические сигналы (токи или напряжения) пред­ставляют собой, как правило, сложные функции времени. Поэтому для анализа и сравнения различных сигналов стремятся использовать такие их значения, которые характеризовали бы сигналы любой формы. Наи­более распространенными явля­ются следующие значения (параметры) напряжений и токов: амплитуд­ное, среднее, средневыпрямленное и среднеквадратическое. Рассмотрим суть этих значений применительно к напряжению.

Амплитудное (пиковое) значение представляет собой наибольшее или наименьшее мгновенное значение переменной составляющей сиг­нала за время измерения

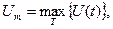(4.1)

где 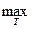- операция нахождения максимального значения сигнала U(t) на интервале измерения Т.

В общем случае положительные и отрицательные пиковые значения переменного напряжения могут быть различными.

Среднее значение (постоянная составляющая) напряжения опреде­ляется выражением

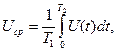(4.2)

где Т₁ - время наблюдения или период электрического колебания; Т₂ - время действия измеряемого напряжения.

Интервалы Т₁ и Т₂ не всегда равны друг другу. При измерении среднего значения импульсных напряжений время действия измеряемого напряжения меньше периода электрического колебания (Т₂ < Т₁).

По физическому смыслу U_сp - это постоянная составляющая сиг­нала U(t) за время Т₁, а графически — это высота прямоугольника с основанием Т₁, площадь которого равна площади, определяемой функ­цией U{t) и осью времени за один .

Средневыпрямленное значение напряжения

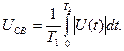(4.3)

Графически U_св - это высота прямоугольника с основанием Т₁, площадь которого равна площади, определяемой функцией U(t) над и под осью времени. При таком определении считается, что операция нахождения средневыпрямленного значения осуществляется с помощью двух полупериодного детектора средневыпрямленных значений. Заме­тим, что для однополярных сигналов U_сp и U_св равны между собой.

Среднеквадратическое значение напряжения - это корень квадрат­ный из среднего значения квадрата напряжения:

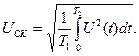(4.4)

Среднеквадратическое значение периодического сигнала сложной формы может определяться также как сумма квадратов постоянной со­ставляющей и среднеквадратических значений отдельных гармоник, т.е.

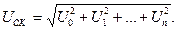(4.5)

Постоянную составляющую U₀ и гармоники U₁,U₂,…U_n нахо­дят путем разложения сложной функции времени U{t) в ряд Фурье.

Пиковое, среднеквадратическое и средневыпрямленное значения на­пряжений сигналов любой формы связаны между собой коэффициента­ми амплитуды К_а, формы K_ф и усреднения K_у:

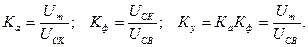(4.6)

Конкретные значения Ка и Кф зависят от формы сигналов и вы­числяются с использованием формул (4.2), (4.3) и (4.4). Например, основные со­отношения между значениями для синусоидального сигнала U(t) = U_msinωt будут равны: