Требования к уровню подготовки студентов. ¾ Знать понятия: электролиты и неэлектролиты, степень диссоциации, сильные и слабые электролиты (примеры)
¾ Знать понятия: электролиты и неэлектролиты, степень диссоциации, сильные и слабые электролиты (примеры), константа диссоциации слабого электролита.
¾ Знать причины отклонения растворов электролитов от закона Рауля и уравнения Вант-Гоффа для осмотического давления.
¾ Знать, что такое изотонический коэффициент, каковы его физический смысл и связь со степенью диссоциации электролита.
¾ Знать особенности состояния ионов в растворах сильных электролитов, понятие кажущейся степени диссоциации.
¾ Иметь представление об активности ионов и активности электролита, коэффициенте активности, его приближенном расчете для разбавленных растворов электролитов через ионную силу раствора.
Задания для самоконтроля
3.5.1 Вычислить изотонический коэффициент и кажущуюся степень диссоциации 2%-ного водного раствора хлорида натрия, если он замерзает
при – 1,26 0С.
3.5.2 Определить кажущуюся степень диссоциации хлорида натрия, если в его 0,12 М растворе при 200С осмотическое давление составляет 500 кПа.
3.5.3 Вычислить, при какой температуре будет замерзать 1%-ный раствор хлорида натрия, если изотонический коэффициент равен 1,92?
3.5.4 Какова активность Ba(NO3)2 в его 0,007 М растворе, если средний коэффициент активности ионов равен 0,74?
3.5.5 Какова величина среднего коэффициента активности ионов в растворе NaCl с ионной силой 0,01 ?
3.5.6 Какова ионная сила 0,021 н. раствора FeCl3 с учетом полной диссоциации соли?
3.5.7 Какова величина среднего коэффициента активности ионов в растворе NaOH с ионной силой 0,0081 ?
3.5.8 Какова активность MgCl2 в его 0,004 М растворе, если средний коэффициент активности ионов равен 0,80 ?
3.5.9 Какие из перечисленных веществ являются слабыми электролитами: а) NH4Cl; б) H2CO3; в) NaCl; г) H2S ?
3.5.10 Какие из перечисленных веществ являются сильными электролитами: а) NaOH; б) H3BO3; в) Ca3(PO4)2; г) KCN? Малорастворимые электролиты не относить ни к сильным, ни к слабым электролитам.
3.5.11 Какова ионная сила 0,03 н. раствора Na2CO3 с учетом полной диссоциации соли?
3.5.12 Какова величина среднего коэффициента активности ионов в растворе ZnSO4 с ионной силой 0,0049 ?
3.5.13 Какова активность Pb(NO3)2 в его 0,01 М растворе, если средний коэффициент активности ионов равен 0,89 ?
3.5.14 Какова ионная сила 0,01 н. раствора ZnCl2 с учетом полной диссоциации соли?
3.5.15 Найдите приближенное значение коэффициента активности для ионов [Fe(CN)6]4 - в растворе с ионной силой 0,0001.
3.5.16 Вычислить активность Ba(NO3)2, а также среднюю активность его ионов в растворе, если средний коэффициент активности ионов f±=0,74, а концентрация соли в растворе составляет 0,006 моль/л.
3.5.17 Определить активность CuSO4 в водном растворе, если для приготовления раствора на 1000 г воды взяли 1,5 г CuSO4.
Лабораторная работа №4
Изучение взаимной растворимости жидкостей в трехкомпонентной системе с ограниченной растворимостью в жидком состоянии
Цель: наблюдение за полной и частичной растворимостью трех жидкостей друг в друге, за появлением порога нерастворимости; ознакомление с методом представления состава трехкомпонентной системы на плоскости в виде треугольной диаграммы Гиббса-Розебома и построение изотермы растворимости.
Оборудование и реактивы: ацетон и толуол (ацетон можно заменить этиловым спиртом, а толуол – хлороформом, ксилолом, четыреххлористым углеродом), дистиллированная вода, 8 конических колбочек на 25 или 50 мл с пробками, которые можно заменить демонстрационными пробирками, бюретка, две мерные пробирки, две пипетки на 1 мл с резиновой грушей для забора жидкости и градуировкой по долям миллилитра.
Теоретические пояснения
При сливании вместе трех жидкостей А, В и С при ограниченной растворимости может наблюдаться три основных типа их распределения друг в друге:
¾ ни одна из жидкостей полностью не растворяется в другой и вещества А, В и С дают три пары частично смешивающихся друг с другом жидкостей: А в В, А в С и В в С;
¾ одна из жидкостей (например, А) полностью растворяется в другой (например, В) и тогда могут возникнуть только две частично растворимые пары: А в С и В в С;
¾ одна из жидкостей (например, А) полностью растворяется как в жидкости В, так и в жидкости С, тогда может возникнуть только одна пара частично смешивающихся друг с другом жидкостей: В в С.
В настоящей лабораторной работе рассматривается последний случай распределения. Установлено, что для систем такого типа увеличение концентрации компонента А приводит к повышению взаимной растворимости компонентов В и С вплоть до образования гомогенной системы.
Для построения диаграммы состояния трехкомпонентной системы требуется четыре координаты: давление, температура, доли двух компонентов из трех, отражающие состав системы.
Для представления состояния трехкомпонентной системы на плоскости необходимо принять условие постоянства температуры и давления. Состав же тройной системы удобно выражать при помощи треугольной диаграммы Гиббса-Розебома, показанной на рисунке 4.1.
Вершины равностороннего треугольника соответствуют чистым веществам А, В и С. Точки на сторонах треугольника отвечают составам двухкомпонентных систем А-В, А-С, В-С. Каждая точка внутри треугольника отражает состав тройной смеси.
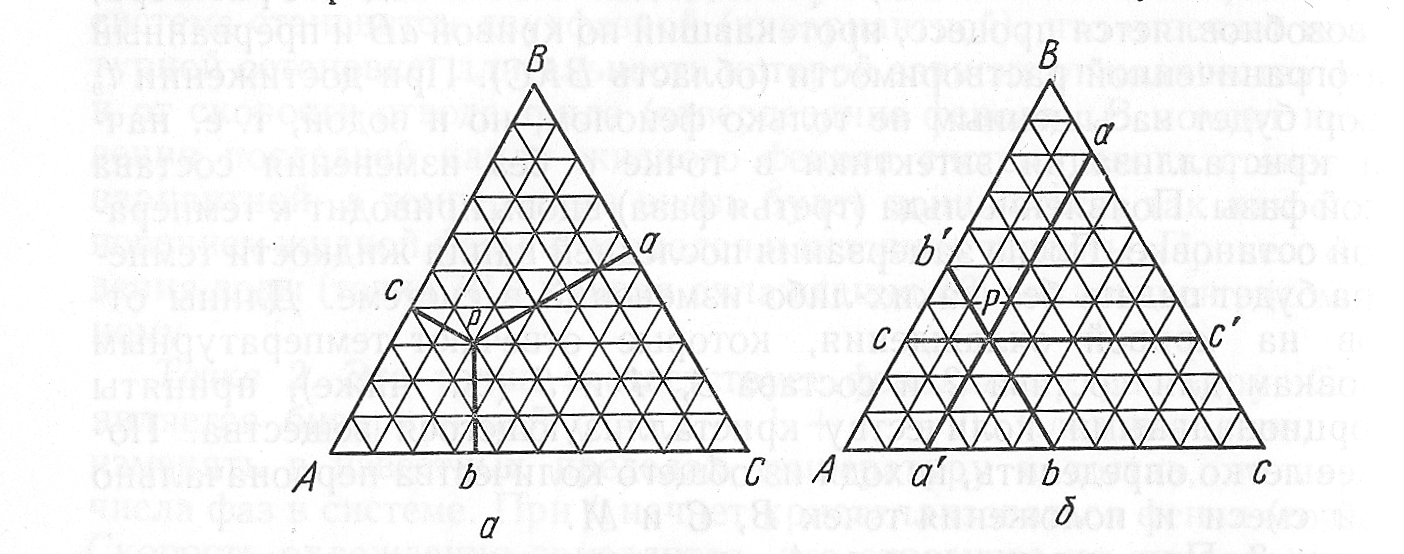
Рисунок 4.1 – Выражение состава трехкомпонентной системы: а) по методу Гиббса; б) по методу Розебома
Существует два метода определения состава по треугольной диаграмме. По методу Гиббса за 100% принимается высота правильного треугольника. При этом сумма длин перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, есть величина постоянная, равная высоте этого треугольника.
Процентное содержание каждого компонента определяется расстоянием от точки Р, отражающей состав системы, до стороны треугольника, противолежащей вершине, соответствующей чистому компоненту.
На рисунке 4.1а отрезок Ра соответствует процентному содержанию компонента А, отрезок Рb – содержанию компонента В, отрезок Рс – содержанию компонента С.
По методу Розебома (рисунок 4.1б) за 100% принимается длина стороны правильного треугольника. Сумма длин трех отрезков, проведенных параллельно сторонам треугольника из точки Р (Ра+ Рb+ Рс) равна стороне треугольника. Содержание компонента А соответствует длине отрезков Ра=bC=Вb'=ac', соержание компонента В соответствует длине отрезков Pb=a'b=Ac=Сc', для компонента С содержание соответствует длине отрезков Рc=Aa'=b'с=Bа.
Оба метода приводят к одинаковым результатам, так как стороны и высоты равностороннего треугольника пропорциональны друг другу.
