Оцінка випадкових похибок опосередкованих вимірювань
Оцінку випадкових похибок опосередкованих вимірювань необхідно здійснювати за такою методикою:
1. Визначити для результатів прямих вимірювань 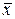 і
і 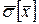 ;
;
2. Визначити значення невідомої величини 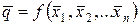 ;
;
3. Обчислити частинні випадкові похибки опосередкованих вимірювань
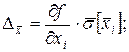
4. Знайти оцінку СКВ результату опосередкованих вимірювань
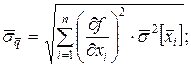
5. Знайти (табл.1) коефіцієнт kt Стьюдента за заданою довірчою ймовірністю Р і кількістю вимірювань n.
6. Знайти граничні значення випадкової складової похибки, яку приймають за похибку опосередкованого вимірювання
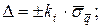
7. Записати результат опосередкованого вимірювання:
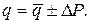
Таблиця 1 – значення коефіцієнта Стьюдента
| n-1 | P=0,95 | Р=0,99 | n-1 | P=0,95 | P=0,99 |
| 3,182 | 5,841 | 2,120 | 2,921 | ||
| 2,776 | 4,604 | 2,101 | 2,878 | ||
| 2,571 | 4,032 | 2,086 | 2,845 | ||
| 2,447 | 3,707 | 2,074 | 2,819 | ||
| 2,367 | 3,500 | 2,064 | 2,797 | ||
| 2,306 | 3,335 | 2,056 | 2,779 | ||
| 2,262 | 3,250 | 2,048 | 2,763 | ||
| 2,228 | 3,169 | 2,043 | 2,750 | ||
| 2,179 | 3,055 | ||||
| 2,145 | 2,977 | ∞ | 1,960 | 2,576 |
Для визначення похибки результату опосередкованого вимірювання необхідно застосувати такі правила:
1. Якщо результат вимірювання представляється сумою або різницею двох і більше виміряних величин:
q = x +…+ z – (u +…+ w),
і похибки Δх, …, Δw незалежні і випадкові, то абсолютна похибка результату може бути визначена за формулою
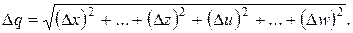
Коли похибки аргументів корельовані, значення Δq може перевищувати отримане за попередньою формулою, але завжди буде задовільняти умову
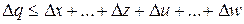 .
.
2. Якщо кінцевий результат вимірювання представляється добутком або часткою двох і більше виміряних значень:
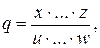
і похибки δх,…,δw незалежні і випадкові, то відносна похибка результату опосередкованого вимірювання визначається
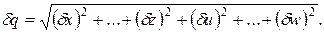
3. Якщо результат опосередкованого вимірювання є функцією однієї величини, q = f(x), то похибка результату визначається
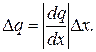
4. В загальному випадку похибка функції декількох величин q = f(x, y, …, w), похибки яких незалежні і випадкові, знаходяться
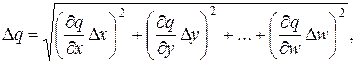
але сумарна похибка ніколи не перевищить значення
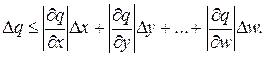
Приклади
Приклад №1
Обчислити щвидкість осідання частинок кремнезему у воді, коли: радіус частинки рівний 2мкм, густина частинки - 3120 кг/м3, густина води - 1000 кг/м3, динамічна в¢язкість води - 1005мкПа×с.
Дано:
r = 2мкм=2·10-6м
ρ = 3120 кг/м3
ρ0 = 1000 кг/м3
η = 1005мкПа×с = 10,05·10-4 Па×с
υ - ?
Розв’язок
Швидкість седиментації частинок описується формулою:. 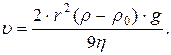
Оскільки в наших умовах прискорення, яке надається частинкам рівне прискоренню вільного падіння то:
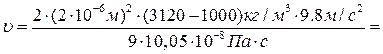 1,84 м/с.
1,84 м/с.
Відповідь: v = 1,84 м/с.
Приклад №2
При розділенні двохкомпонентної суміші на хроматографічній колонці довжиною 50 см було встановлено, що швидкості руху компонентів А і В вздовж колонки відповідно рівні: 2×10-5 м/с і 6×10-6 м/с. Визначити константу розділення для цих компонент.
Дано:
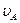 =2×10-5 м/с
=2×10-5 м/с
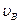 =6×10-6 м/с
=6×10-6 м/с
L=50 см =0,5м
________________
Крозд. - ?
Розв’язок
Константа розділення рівна відношенню часу затримки компонентів суміші, тобто:
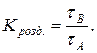 Час затимки компоненту визначається:
Час затимки компоненту визначається: 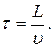 Тоді:
Тоді: 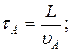
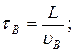
Отже: 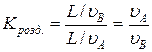 ;
; 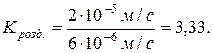
Відповідь: Крозд. = 3,33.
Приклад №3
При проходжені світла через шар 10% -ного розчину цукру товщиною 10 см площина поляризації світла повернулась на кут 16,50, а при поляриметрії розчину невідомої концентрації, з товщиною шару 25 см, площина поляризації повернулась на кут 33,00. Визначити концентрацію досліджуваного розчину.
Дано:
с = 10%
l = 10 см
l1 = 25 см
β = 16,50
β1 = 33,00
____________
с1 - ?
Розв’язок
При поляриметричних дослідженнях концентрація розчину визначається за формулою:
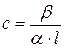 , де: α – питоме обертання площини поляризації, β –кут обертання площини поляризації розчином, l – товщина кювети. Тоді:
, де: α – питоме обертання площини поляризації, β –кут обертання площини поляризації розчином, l – товщина кювети. Тоді: 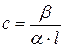 , а
, а 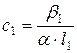 . Розділимо с на с1:
. Розділимо с на с1:
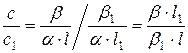 . Отже:
. Отже: 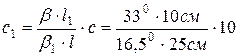 % = 8%.
% = 8%.
Відповідь: с1 = 8%.
Приклад №4
При фотометрії калібровочних розчинів іонів міді Си2+ в присутності диетилдитіокарбамінату свинцю з хлороформом отримали такі значення оптичної густини:
| с ммоль/л | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 |
| D | 0,06 | 0,11 | 0,14 | 0,20 | 0,25 | 0,31 | 0,36 | 0,40 | 0,43 | 0,45 | 0,46 |
За даними таблиці побудувати графік залежності оптичної густини розчину D від концентрації іонів заліза c і графічно визначити, в межах яких концентрацій залежність D = f(c) відповідає основному закону світлопоглинання.
Розв’язок
За даними таблиці будуємо графік залежності оптичної густини розчину D від концентрації іонів міді c ммоль/л:
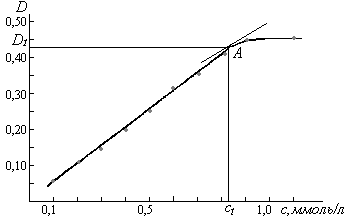
Методом дотичних знаходимо на графіку точку А(C1;D1) - точку початкового нахилу кривої. До цієї точки залежність D = f(c) носить прямопропорційний характер. Проводимо перпендикуляр і графічно знаходимо значення кординати С1 = 0,83 ммоль/л.
Відповідь: В межах концентрацій 0,10 ≤ С ≤ 0,83 ммоль/л залежність D = f(c) носить прямолінійний характер і відповідає закону Бугера – Ламберта – Бера.
Приклад №5
При поляриметрії калібровочних розчинів глюкози отримали такі значення кута обертання площини поляризації:
| с г/100мл | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 |
| β0 | 39,3 | 44,3 | 49,2 | 54,1 | 59,0 | 63,9 | 68,8 | 73,7 | 78,7 |
Накреслити графік залежності β = f(c) і графічно визначити концентрацію досліджуваного розчину глюкози, який обертає площину поляризації світла на кут β1 = 63,50.
Розв’язок
За даними таблиці будуємо графік залежності кута повороту площини поляризації β від концентрації глюкози в розчині c г/100мл.
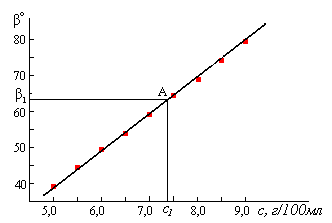
За значенням величини β1 = 63,50 знаходимо на графіку β = f(c) точку А(с1; β1). З точки А проводимо перпендикуляр до осі абсцис і знаходимо значення с1 = 7, 4 г/100мл.
Відповідь: с1 = 7,4 г/100мл.
Приклад №6
При кондуктометричному титруванні 100 мл розчину НСl 0,8 нормальним розчином NaОН отримали такі дані:
| VNaOH, 10-5м3 | 0,25 | 0,50 | 0,75 | 1,00 | 1,25 | 1,50 |
| χ, Ом-1 | 0,030 | 0,025 | 0,018 | 0,016 | 0,017 | 0,019 |
Побудувати криву титрування, знайти точку еквівалентності і визначити концентрацію розчину соляної кислоти.
Розв’язок
За даними таблиці будуємо криву титрування зміни провідності титрованого розчину χ від об’єму добавленого титрату.
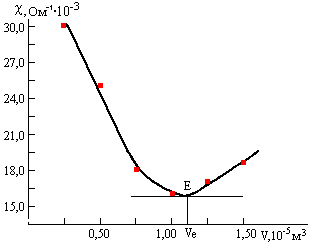
На кривій χ = f(V) методом дотичних знаходимо точку еквівалентності Е, і провівши перпендикуляр на вісь абсцис, знаходимо еквівалентне значення об’єму титрату, що пішов на титрування соляної кислоти в розчині Ve = 1,12·10-5 м3, тобто 11,2 мл. Знаючи об’єм Vе і концентрацію се титрату знаходимо за формулою титрування 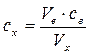 концентрацію досліджуваного розчину сх.
концентрацію досліджуваного розчину сх.
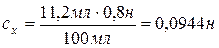 .
.
Відповідь: сх = 0,0944моль/л.
Приклад №7
При потенціометричному окисно-відновному титруванні 50 мл розчину хлориду трьохвалентного заліза 0,1н розчином хлориду двохвалентного олова отримали такі дані:
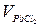 мл мл | |||||||||||
| Е, мВ |
Побудувати криву титрування, знайти еквівалентний об’єм і визначити концентрацію розчину хлориду заліза.
Розв’язок
За даними таблиці будуємо криву титрування зміни окисно-відновного потенціалу титрованого розчину Е від об’єму добавленого титрату.
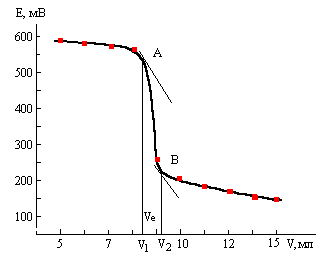
Методом дотичних знаходимо точки А і В максимального перегину кривої титрування. Проводячи перпендикуляри на вісь абсцис знаходимо значення V1 =8,3мл і V2 =9,1мл. За формулою знаходимо еквівалентний об’єм титрату:
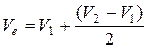 ,
, 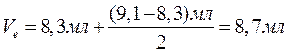 .
.
Знаючи об’єм Ve і концентрацію титрату се знаходимо концентрацію досліджуваного розчину сх за формулою титрування 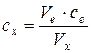 .
. 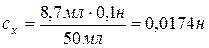 .
.
Відповідь: сх = 0,0174моль/л.
Приклад №8
Обчислити концентрацію іонів міді сх в досліджуваному розчині методом стандартних розчинів, якщо оптична густина досліджуваного розчину Dx = 0,42, а оптична густина та концентрація стандартного розчину відповідно рівні: Dст. = 0,20 ; сст.=0,3 ммоль/л.
Дано:
Сст. = 0,3 ммоль/л
Dст. = 0,20
Dx = 0,42
____________
сх - ?
Розв’язок
Знаючи оптичну густину і концетрацію стандартного розчину, концентрацію досліджуваного розчину визначаємо за формулою: 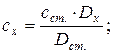
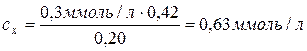 .
.
Відповідь: сх = 0,63 ммоль/л.
Приклад №9
При полярографічному дослідженні 40 мл розчину солі срібла висота полярографічної хвилі рівна Нх = 18 мм, а при додаванні в полярографічну комірку 20 мл стандартного розчину цієї солі, висота полярографічної хвилі збільшилась на 7 мм. Знайти концентрацію сх іонів срібла в досліджуваному розчині методом добавок, якщо концентрація стандартного розчину сст. = 8·10-4 мг/мл.
Дано:
сст. = 8·10-4 мг/мл
Нх = 18мм
ΔН = 7мм
Vст. = 20мл
Vх = 40мл
____________
сх - ?
Розв’язок
Концентрацію досліджуваного розчину обчислюємо методом стандартних добавок за формулою: 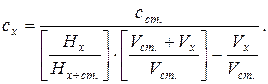
де: сх і сст. – концентрації досліджуваного і стандартного розчинів, Hx – величина півхвилі досліджуваного розчину, Hx+ст. – величина півхвилі досліджуваного розчину після додавання до нього стандартного розчину, Vx і Vст. – об’єми досліджуваного і стандартного розчинів.
Знаходимо Нх+ст. = 18мм + 7мм = 25мм і обчислюємо концентрацію
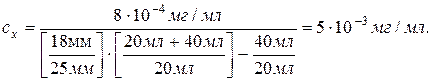
Відповідь: концентрація іонів срібла рівна 5·10-3 мг/мл.
Приклад №10
Знайти концентрацію розчину піперидину, якщо рН такого розчину визначений потенціометрично рівний рН = 7,5, а ступінь дисоціації основи α = 0,28.
Дано:
рН = 7,5
α = 0,28
____________
сх - ?
Розв’язок
Знаючи рН розчину основи, знайдемо рОН цього розчину за формулою: рОН = 14 – рН. Отже: рОН = 14-7,5 = 6,5. За величиною рОН знаходимо концентрацію [ОН-] в розчині піперидину.
Оскільки 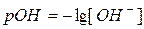 , то [ОН-] = 10-6,5моль/л = 3,16·10-7моль/л.
, то [ОН-] = 10-6,5моль/л = 3,16·10-7моль/л.
Знаючи концентрацію іонів гідроксилу і ступінь дисоціації піперидину знайдемо його концентрацію в розчині, яка буде рівна: 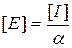 , де: [Е] – концентрація електроліту, [I ] – концентрація іону, α – ступінь дисоціації електроліту.
, де: [Е] – концентрація електроліту, [I ] – концентрація іону, α – ступінь дисоціації електроліту.
Отже:  .
.
Відповідь: в досліджуваному розчині концентрація піперидину рівна 1,13·10-6моль/л.
Приклад №11
Обчислити відносну, динамічну і кінематичну в¢язкість ефірної олії на основі вимірювань часу падіння кульки по методу Стокса, коли:
густина ефірної олії – 0,920 г/см3;
густина стандарту - 0,948 г/см3;
густина кульки – 7,87 г/см3;
динамічна в¢язкість стандарту - 9,86 Пз;
час падіння кульки в олії - 32 с;
час падіння кульки в стандарті – 48 с.
Дано:
ρк= 7,87 г/см 3
ρст.= 0,948 г/см3
ρр= 0,920 г/см3
ηст. = 9,86Пз
tст. = 48с
tх. = 32с
____________
ηх - ?
Розв’язок
Відносну в¢язкість за методом Стокса визначають за формулою: 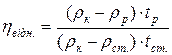 . Де: ρк – густина кульки, ρр - густина досліджуваної рідини, ρст. – густина рідини стандарту, tст. – час падіння кульки в рідині стандарту, tр - час падіння кульки в досліджуваній рідині.
. Де: ρк – густина кульки, ρр - густина досліджуваної рідини, ρст. – густина рідини стандарту, tст. – час падіння кульки в рідині стандарту, tр - час падіння кульки в досліджуваній рідині.
Отже: 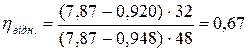 . Динамічна в¢язкість
. Динамічна в¢язкість 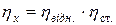 = 0,67·9,86Пз =6,61Пз = 0,661Па·с.
= 0,67·9,86Пз =6,61Пз = 0,661Па·с.
Кінематична в¢язкість рівна 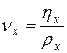 =
= 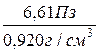 =7,18Ст = 7,18·10-4м2/с.
=7,18Ст = 7,18·10-4м2/с.
Відповідь: динамічна в¢язкість ефірної олії рівна 0,661Па·с, а кінематична - 7,18·10-4м2/с.
