Кинетика процесса цементации

Скорость процесса цементации при отсутствии побочных реакций выражается массой вытесняемого металла, осевшего на поверхности вытесняющего металла в единицу времени, или массой вытесняющего металла, переходящего в ионное состояние. Поскольку при токе I (А), протекающем от катодных участков к анодным, скорость (моль/с) процесса катодного восстановления ионов или анодного окисления металла выражается отношением I/zF, то именно эта величина и будет скоростью процесса цементации. С другой стороны, если цементацию ведут при постоянном объеме электролита V (м³), то уменьшение массы вытесняемого металла в единицу времени составит –VdC₂/dτ (где C₂ — концентрация ионов вытесняемого металла) и основное уравнение процесса цементации запишется так:

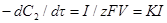
где К = 1/zFV.

Заменим в этом уравнении ток I плотностью тока i = I/S (здесь S — поверхность, м²):

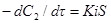
Это уравнение справедливо во всех случаях, когда отсутствуют побочные реакции. В более общем виде уравнение скорости можно

записать так:

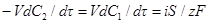
Здесь С₁ — концентрация ионов вытесняющего металла.

Для решения уравнения необходимо все величины, которые могут изменяться со временем, выразить через функции, связывающие изменение этих величин с изменением концентрации ионов вытесняемого металла. В связи с разнообразием контролирующих стадий процесса и их возможной сменой в ходе цементации описание всех случаев кинетики цементации единым уравнением не пред- ставляется возможным. Поэтому рассмотрим наиболее важные уравнения скорости цементации для главного периода, отвечающие той или иной контролирующей стадии *.

Случай 1. Скорость контролируется процессом восстановления ионов вытесняемого металла, протекающим на предельном токе. Осаждение идет на внешней поверхности катодных участков. Катодная поверхность все время остается постоянной.

Подставим в основное уравнение кинетики выражение для предельного тока диффузии:

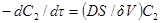
Если толщина δ диффузионного слоя не изменяется, т. е. процесс идет при постоянных гидродинамических условиях, то в правой части уравнения все величины в скобках постоянны и

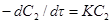
Интегрирование уравнения приводит к выражению:

ln С₂ = – Κτ + const

При τ = 0 концентрация ионов вытесняемого металла равна начальной их концентрации 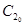откуда

const = ln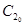

и окончательно:

ln С₂ = ln 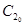– Κτ

Это уравнение оправдывается в большом числе случаев как в условиях неопределенного гидродинамического режима (например, при вытеснении ионов селена медью по данным В. К. Гаркуна и И. А. Кузина, приведенным на рис. 14.16), так и при проведении процесса на вращающемся диске. В последнем случае, как установили М. А. Епископосян и И. А, Каковский на примерах цементации ионов меди и серебра железом, подтверждается требуемая теорией зависимость скорости процесса от корня квадратного из скорости вращения диска, соответствие рассчитанных и экспериментальных значений констант скоростей и, наконец, значение энергии активации (12 — 16 кДж/моль), характерное для процессов, контролируемых диффузией.

* В процессе цементации коэффициент активности, как правило, изменяется незначительно. Поэтому в этом разделе активности заменены концентрациями.

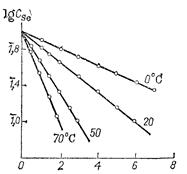
Рис. 14.16. Зависимость логарифма остаточной концентрации селена от времени цементации.

Случай 2. Разряд ионов вытесняемого металла происходит при предельном токе на внешней поверхности вытесняемого металла, но значение активной поверхности обратно пропорционально количеству осевшего металла. Тогда

S = K₁/( 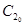– C₂)

и после разделения переменных уравнение –dC₂/dτ = (DS/δV)C₂ превращается в

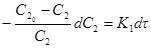
Записываем это уравнение в виде

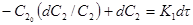
и после интегрирования получаем

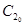– ln C₂ + C₂ = K₁τ + const

Как и раньше, при τ = 0 С₂ = 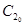. Тогда

const = – 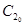ln +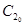

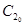
Следовательно

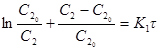
и окончательно

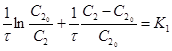
Это уравнение, выведенное Б. В. Дроздовым, охватывает случай цементации ионов меди из сульфатного раствора никелевым порошком (рис. 14.17).

Случай 3. Восстановление ионов вытесняемого металла происходит на наружной поверхности, а скорость процесса определяется диффузией ионов вытесняющего ме-талла через поры цементного осадка.

В начальный период цементации увели- чивается концентрация ионов вытесняемого

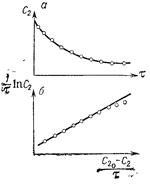
Рис. 14.17. Проверка уравнения Дроздова на примере цементации ионов меди никелем:

а — зависимость концентрации ионов меди от времени; б —тоже в координатах Дроздова.

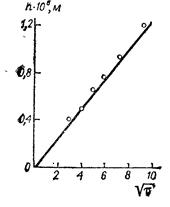
Рис. 14.18. Проверка уравнения Бермана на примере цементации ионов меди железом.

h — толщина слоя меди, пропорциональная уменьшению концентрации ионов меди в электролите.

металла у его поверхности и достигает величины, близкой к насыщению. Диф-фузия в раствор происходит со скоростью (D₁/δ)( 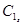– C₁). Поскольку концентрация C₁ изменяется в течение опыта незначительно, можно принять ( 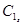– C₁) = const. Толщина диффузионного слоя изменяется во времени пропорционально количеству сцементированного металла ( 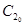– C₂).

Тогда

– dC₂/dτ = K/( 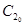– C₂) и 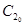dC₂ – C₂dC₂ = – Kdτ

Интегрирование дает:

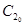C₂ – ½C₂² = – Kτ + const

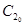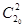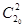При τ = 0 С₂ = . Следовательно, const = ½ и – 2 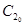С₂ + + C₂² = 2Kτ или 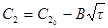. Это уравнение впервые предложил И. А. Берман. Его справедливость подтверждается рис. 14.18.

Случай 4. Осаждение происходит на внешней поверхности вытесняемого металла. Омическое сопротивление пренебрежимо мало. Следовательно, поверхность эквипотенциальна. Скорости как катодной, так и анодной реакций определяются практически целиком электрохимической поляризацией. Поверхности, на которых протекают катодная и анодная реакции, все время остаются постоянными. Область потенциалов при цементации достаточно удалена от потенциалов чистых металлов, так что скоростями обратных реакций в кинетических уравнениях можно пренебречь. При соблюдении указанных допущений

I_k = I_a

причем

I_k = i_kS_k; I_a = i_aS_a

Для плотности катодного и анодного токов напишем кинетические выражения теории замедленного разряда в виде:

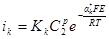и 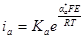Здесь р — порядок реакций; α_к* и α_а* — кажущиеся коэффициенты переноса.

Запишем для тока:

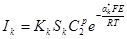и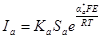

Прологарифмируем эти выражения и исключим из них потенциал

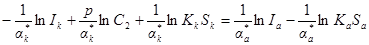
С учетом выражения I_к = I_a получим

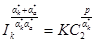или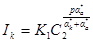

Подставив значение I_к в основное уравнение, имеем:

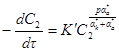
Здесь в константу K’ собраны все постоянные величины. Выражение получили В. Л. Хейфец и А. Л. Ротинян.

Отличительной особенностью данного уравнения является зависимость порядка реакции от величин коэффициентов переноса и порядка катодной реакции по восстанавливающимся ионам. Если p = 1 (что наиболее часто встречается), то уравнение приводит к дробному показателю степени у концентрации С₂. И только при α_k* = 0, т. е. если допустить, что катодный процесс протекает в режиме безактивационного разряда, скорость реакции цементации будет первого порядка. Довольно часто при двухэлектронной суммарной реакции катодный процесс восстановления ионов металла протекает при замедленной стадии присоединения первого электрона (α_к* = 0,5), а анодный — при замедленной стадии отщепления второго электрона (α_а* = 1,5), В этом случае показатель степени у концентрации оказывается равным ³/₄, если р = 1, и ³/₂, если р = 2, т. е. если в катодном процессе участвуют двухъядерные комплексы цементируемого металла.

М. И. Алкацев установил, что при цементации ионов меди железом в условиях воздействия на электролит ультразвука зависимость скорости процесса от концентрации ионов меди в растворе перестает быть прямолинейной, т. е. уравнение скорости первого порядка перестает оправдываться (рис. 14.19, а). Это может быть обусловлено тем обстоятельством, что в условиях ультразвукового перемешивания процесс не контролируется диффузионными ограничениями. Тогда можно ожидать, что скорость процесса будет определяться электрохимическим контролем. Если это предположение справедливо, то в координатах lg i — lg C кривая рис. 14. 19, а должна превратиться в прямую линию.

Прямая на рис. 14.19, б действительно подтверждает приведенное выше предположение, причем тангенс угла наклона равен 0,7. Таким образом, эти данные свидетельствуют о том, что в условиях

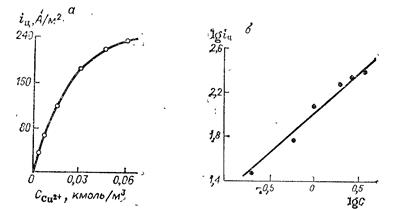
Рис. 14.19. Проверка уравнения на примере цементации ионов меди железом из подкисленного сульфатного раствора в условиях перемешивания раствора ультразвуком:

а — зависимость скорости цементации i_ц от концентрации ионов меди 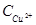; б — то же в логарифмических координатах.

опытов процесс контролируется электрохимическими стадиями, причем в катодном процессе восстановления ионов меди замедленным является присоединение первого электрона, а в анодном процессе ионизации атомов железа — отщепление второго электрона.