Математикалық формуласы
Карно принципі бойынша жылу машинасы жұмыс жасауы үшін жылу көзі кемінде екеу болуға тиісті : бірі-қыздырғыш, екіншісі – суытқыш. Бірінің Т1 , екіншісінің температурасы (Т2 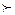 Т2). Жұмыскер дене идеал газды қарастырайық. Газ поршеньді целиндрге орналассын, көлемі V1 . Целиндрдің поршені ешқандай үйкеліссіз, яғни идеал жағдайларда қозғалады дейік. Жылу машинасының п.ә.к. және машина жұмысының тиімділігі қандай факторларға байланысты ? Бұл сұраққа француз инженері Карно идеал машинаны қарастыру арқылы жауап берген, сөйтіп өзінің Карно принципін ұсынған.
Т2). Жұмыскер дене идеал газды қарастырайық. Газ поршеньді целиндрге орналассын, көлемі V1 . Целиндрдің поршені ешқандай үйкеліссіз, яғни идеал жағдайларда қозғалады дейік. Жылу машинасының п.ә.к. және машина жұмысының тиімділігі қандай факторларға байланысты ? Бұл сұраққа француз инженері Карно идеал машинаны қарастыру арқылы жауап берген, сөйтіп өзінің Карно принципін ұсынған.
12- суретте (б) идеал жылу машинасының жұмысы график арқылы көрсетілген. Мұнда а нүктесінде газдың көлемі – V1 , температурасы–Т1.
Осы газға Т1 температуралы жылу көзін қосайық. Жылу көзінен алынған жылудың шамасы Q1 жұмысқа айналып газдың көлемін V1-ден V2 дейін ұлғайтады, демек поршень жоғары көтеріліп A1 жұмысы өндіріледі. Тұрақты температурада (T1=const) идеал газдарда өндірілетін ұлғаю жұмысы
A1=RT1lnV2/V1, Q1=A1,
осыдан A1=Q1=RT1lnV2/V1
Графикте бұл процесс ab қисығымен көрсетілген, оның астындағы V1abV2 аудан A1 жұмыстың мәніне тең, ab қисығы изотерма деп аталады.
b нүктесінде жылу көзі жоқ болғанда газдың көлемін V3-ке дейін ұлғайтайық. Сырттан жылу берілмей өтетін процесс адиабатты процесс болады, bс қисығы адиабата деп аталады. Бұл жағдайда ұлғаю жұмысы жүйенің өз жылуы нәтижесінде жасалатындықтан жүйе суыйды. Яғни газ суып температурасы Т1-ден Т2 дейін төмендейді. Жүйе с нүктесіне келеді.
Бұл кездегі жұмыс A2=cv(T1-T2), мұнда cv –жылу сыйымдылық с нүктесінде жұмыскер дене Т2 температурада суытқышқа Q2 жылуды береді. Осының нәтижесіндегі жұмыс арқылы газ сығылып көлемі V3–тен V4 дейін азаяды.
Газды сығуға жұмсалған жұмыс А3
A3=Q2=-RT2lnV3/V4
A1 және A3 жұмыстардың бір-біріне айырмашылығы мынадай: бірі жүйеде жасалған жұмыс болса (А1), екіншісі жүйеге сырттан жұмсалған жұмыс (А3). Термодинамикада сырттан жұмсалған жұмыс теріс таңбамен алынады[1].
Жылу қозғалтқышының жұмысы міндетті түрде циклді болуы керек. Карно машинасының жұмысы циклді болуы үшін жүйені d нүктесінен а нүктесіне қайтып оралтуымыз керек. Ол үшін d нүктесінде жылу көзі жоқ болғанда адиабатты сығылу процесін жүргізіп көлемді V4-ден V1-дейін азайтамыз. Адиабатты процестерде жүйеге жылу сырттан берілмейтіндіктен ішкі энергиясы есебінен жұмыс істейді. Бұл кезде ішкі энергия азаяды:
A4=cv(T2-T1), T1>T2
болғандықтан A4=-cv (T1-T2)
Жүйедегі өндірілген жалпы жұмыс барлық жұмыстардың қосындысына тең, ал график бойынша (2-сурет, б) циклдің ауданына тең:
Ажалпы=A1+A2+A3+A4=Q1-Q2=RT1ln(V2/V1)-RT2ln(V4/V3)
Идеал газдың адиабаттық процесінің заңдары бойынша:
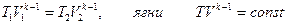
Графикте V2 жәнеV3 бір адиабатаға жатады, оларға сәйкес температуралар Т1 және Т2. Бұл шамалар үшін:
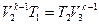
Бұл қатынастарды бір-біріне бөлгенде:
V2/V1=V3/V4
Сонда
Ажалпы=RT1ln(V2/V1)-RT2ln(V3/V4)=Rln(V2/V1)(T1-T2)
Жылу машинаның п.ә.к. жұмсалған жылудың қандай бөлігі пайдалы жұмысты беретіндігін көрсетеді:
п.ә.к. 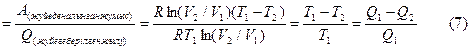
Мұнда Q1 – қыздырғыштан алынған жылу; Q2 – суытқышқа берілген жылу.
(IV.1) – теңдеу бойынша жылу қозғалтқыштардың п.ә.к. қыздырғышпен суытқыштың температураларының айырымына байланысты. Бұл айырымның үлкендігіне байланысты п.ә.к. өседі. Яғни, жылу қозғалтқыштың тиімділігі қыздырғыш пен суытқыштың температураларына тәуелді. Бірақ жылу қозғалтқыштың п.ә.к. үнемі бірден кем болады.
Жоғарыда қарастырған процесте жылу қыздырғыштан поршеньді цилиндрге өздігінен ауысып жұмыс береді. Ал суық денеден ыстық денеге жылу өздігінен ауыспайды. Бұл процесс Карноның кері циклінде өтеді.
Мұны жүргізу үшін жүйеде газдың көлемін адиабаттық жағдайда а нүктесінен d-нүктесіне дейін ұлғайтайық (2-сурет, б). Бұл процесте ішкі энергия өзгереді (азаяды). Жүйенің температурасы Т1-ден Т2 дейін төмендейді. d-нүктеде жүйені жылу көзіне қосамыз. Тұрақты Т2 температурада жүйе көлемі V4-тен V3 дейін ұлғаяды. Бұл кезде жүйе берілген жұмыс есебінен жұмыс жасайды, мұндағы жылудың мәні изотермиялық процестегі жылуға тең. с-нүктесінен b-нүктесіне дейін адиабаттық процесс арқылы газдың көлемін V2 дейін азайтамыз. Бұл кезде ішкі энергия өседі, ал температура Т2-ден Т1 дейін көтеріледі. b-нүктесінен а-нүктесіне дейін
процесті изотермиялық жағдайда жүргіземіз. Бұнда жүйеден сыртқа жылу бөлінеді де, көлемі V2-ден V1-дейін азаяды.
Жүйеде төрт түрлі процесс өтті, тек олардың бағыты тура циклдегі процестерге қарама-қарсы. Q1 мен Q2 айырмасы (Q1 - Q2) сырттан жұмсалғанжұмыс әсерінен туады. Сөйтіп жылу суық денеден ыстық денеге ауысты, бірақ бұл процесс өздігінен жүрмей сыртқы жұмыстың нәтижесінде жүреді. Карноның тура цикліндегі пайдалы процесс – жылудың бір бөлігінің жұмысқа айналуы, ал қатар өтетін пайдасыз процесс (компенсация) – жылудың қалған бөлігінің суытқышқа берілуі болады.
Карноның кері цикліндегі пайдалы процесс – жылу алынуы, ал сырттан жүйеге жұмыс жұмсалынуы (компенсация) пайдасыз процесс. Мұндай процестерге мұздатқыштардың жұмыс істеуі негізделген.
Карно циклінде жұмыскер дене ретінде идеал газ қарастырылғандықтан, ондағы процестердің бәрі идеал жағдайда өтеді. Бұдан шығатын қорытынды: п.ә.к. бірден кем (п.ә.к.<1). Ал реал жүйелерде п.ә.к. одан да кіші болуға тиісті, себебі реал процестерде жылу қосымша кедергілерге, мысалы, үйкеліске қарсы жұмсалады. Карно циклінде өтетін процесс қайтымды, ал оның жұмысы максимал. Реал жүйеде қайтымсыз процестер өтетіндіктен ондағы өндірілетін жұмыс Карно цикліндегіден аз.
Карно циклінен термодинамиканыңекінші заңының негізгі теңдеуін алдық. Бұл теңдеу жылу машиналарының пайдалы әсер коэффициентінің (п.ә.к.=h) қыздырғышпен суытқыш температуралараның айырмасына ғана байланысты екенін көрсетеді.
h=(Q1-Q2)/Q1=(T1-T2)/T1
Біз жоғарыда екінші заң процестің өту-өтпеуін, оның бағытын, шегін көрсетеді дедік. Мұндай проблемаларды шешу жолында Клаузиус екі теорема ұсынады. Бұл теоремалар Карно циклінен алынған қорытындыларға негізделген. Процестің өту бағытын осы теоремалар бойынша табуға болады.
Бірінші теорема.
Жұмыскер дене ретінде идеал газды қолданатын жылу машинасымен қатар тағы бір машина қарастырайық. Бұл машинада жұмыскер дене ретінде идеал газ емес, басқа бір зат, мысалы, бу не сұйық зат алынсын. Екі машинаның да жылу көзі мен суытқышы ортақ және температура аралығы бірдей: Т1 –ден Т2 дейін өзгереді.
Бірінші машина жылу көзінен Q1 жылу алып суытқышқа Q2 жылу берсін. Жасалатын жұмысы А1=Q1-Q2, ал h1=(Q1-Q2)/Q1=(T1-T2)/T1.
Екінші машинаның жылу көзінен алатын жылуы біріншісінің алатын жылуына Q1 тең дейік.
Егер екінші машинаның өндірген жұмысы А’ бірінші машинаның жұмысына А1 тең болса (А’ =А1), бұл екі машинаның п.ә.к. бірдей болғаны (h1=h’). Суытқышқа беретін жылулары да бірдей (Q’2= Q2).
Клаузиус бірінші теореманы ұсынарда мынадай жорамалдау жасады. Екі машитнаның п.ә.к. бірдей емес (h1>h’), онда А1> А’, демек, бірінші машинада жылудың көбірек мөлшері жұмысқа айналады, суытқышқа азырақ мөлшері ауысады (Q2<Q’2). Енді бірінші машинада жасалған жұмысты кері циклмен жұмыс істейтін екінші машинаға жұмсайық. Бұл жағдайда екінші машинаның жұмыскер денесі Т2 температурада көлемін ұлғайтып суытқыштан Q2 жылуды алады, ал Т1 температурада керісінше көлемі сығылып жылу көзіне Q1 жылуды береді. Сөйтіп бірінші машина қыздырғыш ретінде, ал екінші машина мұздатқыш ретінде жұмыс істейді. Мұздатқыш машинасы әрбір циклде А’ жұмысты пайдаланып Q’ жылуды суық денеден ыстық денеге ауыстырады. Бұл ыстық дене бірінші машина үшін жылу көзі болады да, оған Q2 жылудың үстіне тағы да қосымша жылу береді. Толық бір циклде оның жылуы Q’1= Q1 болады.
13-суретте осы машиналардың жұмыс схемасы келтірілген. Бірінші машинаның жұмысы екінші машинаның жұмысынан көп деп жорамалдайық (А>А’). Сонда екі машинадан бір циклде жасалған жалпы жұмыстың таңбасы оң болады (А1-А’) >0, суытқыштан алынған жылу бұл жұмысқа эквивалентті, суытқыш бірінші машинадан Q2 жылуды алса, екінші машинаға жылуды береді. A=Q1-Q2, A’=Q’1-Q’2, Q1=Q’1, сондықтан Q’2-Q=A-A’. Жылу көзінің күйі өзгермейді, себебі ол бірінші машинаға қанша жылу берсе, екінші машинадан сонша жылуды алады.

 T1 Q1 Q’1
T1 Q1 Q’1
 | |||
 |
I II



 A1 A’
A1 A’
 |
T2 Q2 Q’2
13-сурет
Қорытып айтқанда бұл жүйеде жылудың жұмысқа айналуы ешқандай компенсациясыз жүріп тұр. Осыдан Карно машинасының жұбы екінші текті перпетуум-мобиле беретінін көреміз. Демек h1>h2 деген жорамалымыз дұрыс емес, ол термодинамиканың екінші заңына қайшы келеді. Егер, керісінше h1<h’ деп жорамалдасақ, онда жоғарыдағыдай қос машинадан тұратын жүйені құрып, идеал газбен жұмыс істейтін машинаны суытқыш ретінде алсақ, тағы да екінші заңға қайшы келетін қорытынды шығады. Осыдан Клаузиустың бірінші теоремасы шығады: қайтымды Карно машинасының п.ә.к. жұмыскер дененің табиғатына тәуелсіз.
Екінші теорема.
Карно-Клаузиустың бірінші теоремасы бойынша жылу машиналарының п.ә.к. қыздырғыш пен суытқыш температураларының айырмасынан ғана анықталады.
Екінші теорема бойынша берілген температураларда басқа циклдермен салыстырып қарағанда, Карно циклі – ең тиімді цикл. Карно циклі екі адиабатадан және екі изотермадан тұратынын біле отырып, бұл теореманы дәлелдеу үшін (7)-теңдеуді төмендегідей түрлендірейік:
п.ә.к. =h=(Q1-Q2)/Q1=(T1-T2)/T1,
осыдан
Q2/Q1=T2/T1, немесе Q1/T1=Q2/T2
Бір адиабатадан екінші адиабатаға ауысудың жылулары мен температуралары барлық изотермалар үшін бірдей қатынаста болады.
14-суретте белгілі бір жұмыскер дененің беретін циклі келтірілген. Циклді арақашықтықтары бірдей болатын бірнеше адиабаталарға бөлейік. Сонда (ІV.2)-теңдеу бойынша
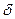 Q1 / Т1 =
Q1 / Т1 = 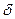 Q2 / T2=
Q2 / T2= 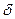 Q3 / Тз=... (IV.3)
Q3 / Тз=... (IV.3)
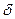 Q1,
Q1, 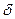 Q2,
Q2, 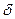 Q3... изотермиялық жағдайда бір адиабатадан көрші екіншісіне ауысу жылулары, ал Т1,Т2,Т3 - осы ауысудың температуралары. Денеге берілген жылудың температураға қатынасы келтірілген жылу деп аталады. 14-суреттегі цикл адиабаталар мен изотермалар арқылы өте көп Карно циклдеріне бөлінген.
Q3... изотермиялық жағдайда бір адиабатадан көрші екіншісіне ауысу жылулары, ал Т1,Т2,Т3 - осы ауысудың температуралары. Денеге берілген жылудың температураға қатынасы келтірілген жылу деп аталады. 14-суреттегі цикл адиабаталар мен изотермалар арқылы өте көп Карно циклдеріне бөлінген.
Жұмыскер дененің жылу көзінен алатын жалпы жылуы
Q1= 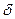 Q'1+
Q'1+ 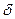 Q'2+
Q'2+ 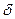 Q'3+...
Q'3+...
Бұдан (ІV.З) - теңдеу бойынша:
Q1=T'1( 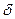 Q'1) / Т 1 + T'2(
Q'1) / Т 1 + T'2( 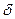 Q'2) / Т2+...
Q'2) / Т2+...
немесе
Q1=(T'1 + T'2+...)( 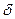 Q'1/T'1)
Q'1/T'1)
Дәл осы сияқты жұмыскер дененің суытқышқа беретін жылуы
Q0= 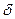 Q'1+
Q'1+ 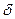 Q'2+
Q'2+ 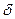 Q'3+...
Q'3+...
Qo=T1( 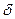 Q1 / T1)+Т2(
Q1 / T1)+Т2( 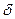 Q2 / Т2)+...
Q2 / Т2)+...
Q0=(T1+T2+T3+...)( 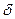 Q1 / Т1)
Q1 / Т1)
Q және Qo мәндерін (ІV.І-теңдеуге қойсақ:
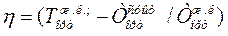
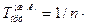 (Т'1+Т'2+Т'3+...)
(Т'1+Т'2+Т'3+...)
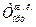 - жылу көзінің орташа абсолюттік температурасы;
- жылу көзінің орташа абсолюттік температурасы;
п -изотермалардың саны.
Бұлар үлкен циклдің жоғарғы шегін көрсетеді (14-сурет). Сол сияқты 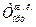 =1 /п(Т1 + Т2+.Тп) бұл суытқыштардың орташа абсолюттік температурасы.
=1 /п(Т1 + Т2+.Тп) бұл суытқыштардың орташа абсолюттік температурасы.
(IV.4) - теңдеу барлық кез келген циклдерге қолданылады. Осыдан пайдалы әсер коэффициенті екі температураға байланысты екені түсінікті
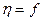 (T1 ,T2)
(T1 ,T2)
Карно-Клаузиус теоремасы универсалды температуралық шкаланы жасауға көмектеседі. Бұрын термометрлердің (мысалы, сынап, спирт, газ термометрлері) шкаласы әр түрлі болған. 1852 ж. ағылшын ғалымы Томсон (лорд Кельвин) температураның термодинамикалық жаңа шкаласын ұсынды. Оны абсолюттік температура шкаласы деп атайды.
(8) – теңдеуді пайдаланып жылулардың бір-біріне қатынасы бүтін аз сандардың қатынастарындай десек, онда қыздырғыш пен суытқыш жылуларының айырмасы төмендегідей болады:
(Q’1-Q1):(Q’2-Q2):(Q’3-Q3)…=1:2:3:…
(Q’1-Q1)/1:(Q’2-Q2)/2:(Q’3-Q3)/3:… =
Температура аралығы бір градусқа тең деп алсақ, онда термометрдегі заттың табиғатына тәуелсіз шкаланы аламыз. Бұл шкала (IV.3) – теңдеудегі, яғни екі түрлі температураның қатынасы қайтымды түрде жұмыс істейтін машинаның қыздырғыштан алатын жылуы мен суытқышқа беретін жылуының қатынастарына тең болатындығына негізделген. Сөйтіп екінші заң температураның әмбебап шкаласы болатынын және температураны абсолюттік нөлден бастап өлшеуге болатынын көрсетті. Температураның әмбебап шкаласы туралы Томсонның ұсынысы тек 1954 ж. физика-химиктердің халықаралық 10-конференциясында қабылданды. Осы конференцияда температураның термодинамикалық шкаласының негізгі нүктесі ретінде судың үштік нүктесі алынсын деген қорытындыға келді. Үштік нүкте судың үш түрлі агрегаттық күйінің (бу, сұйық, мұз) тепе-теңдік нүктесі, бұл нүктенің температурасы 273,16 Кельвин градусына тең деп алынды.
