Распределение ионов в растворе электролита и потенциал ионной атмосферы

Чтобы описать ион-ионное взаимодействие, необходимо знать распределение ионов в растворе и природу сил, действующих между ионами. Поскольку и ионы, и диполи растворителя находятся в хаотическом движении, а ионы могут образовывать ассоциаты, комплексы и недиссоциированные молекулы, то в общем виде задача о распределении ионов оказывается чрезвычайно сложной. Можно предположить, что электролит полностью диссоциирован (α=1), растворитель представляет собой непрерывную среду с диэлектрической постоянной ε, а ионы взаимодействуют в нем только по закону Кулона. В этих условиях вопрос о распределении и взаимодействии ионов в растворах электролитов был решен П. Дебаем и Э. Хюккелем (1923 г.). Среди множества ионов, участвующих в хаотическом тепловом движении, в теории Дебая и Хюккеля выбирается один - так называемый центральный ион, который рассматривается как неподвижный. Иначе говоря, начало выбираемой системы координат привязывается к центру этого иона. Вблизи центрального иона некоторым образом распределяются другие ионы. Характер этого распределения обусловлен, во-первых, полем центрального иона, которое, согласно формуле (2.3.2), убывает с расстоянием r от центрального иона, и, во-вторых, тепловым движением ионов. Поэтому чем ближе к центральному иону, тем больше вероятность того, что там окажется ион противоположного знака (рис. 3.1, а). Центральный ион как бы окружен ионной атмосферой. Выбор центрального иона является условным, т. е.

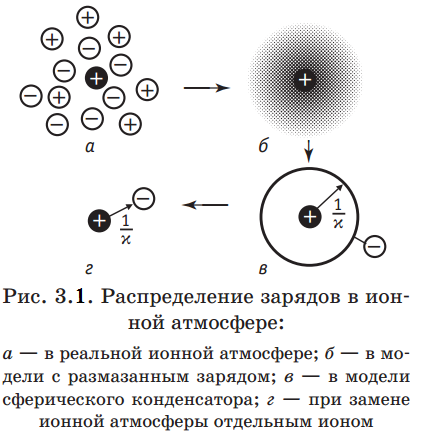Каждый ион можно рассматривать в качестве центрального и в то же время входящего в состав ионной атмосферы других ионов. Тепловое движение ионов в ионной атмосфере приводит к тому, что дискретные заряды этих ионов как бы размазываются. В результате ионную атмосферу, состоящую из отдельных ионов, в среднем за некоторый промежуток времени можно моделировать облаком размазанного заряда, плотность которого ρ уменьшается по мере удаления от центрального иона (рис. 3.1, б). Общий заряд ионной атмосферы из-за условия электронейтральности должен быть по абсолютной величине равен заряду центрального иона z_ie₀ и противоположен ему по знаку.

Первое приближение теории Дебая - Хюккеля соответствует условию точечных ионов, а потому

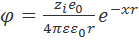. (3.2.1)

Для вычисления ион-ионного взаимодействия представляет интерес не общий потенциал ϕ, а та его часть ϕ_a, которая создается ионной атмосферой в месте расположения центрального иона. Величина ϕ_a называется потенциалом ионной атмосферы. При расчете ϕ_a используют принцип суперпозиции (т. е. наложения) электрических полей, согласно которому для точечных ионов

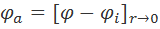, (3.2.2)

где

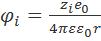(3.2.3)

представляет собой потенциал, создаваемый центральным ионом [см. формулу (2.3.3)]. Подставляя уравнения (3.2.1) и (3.2.3) в (3.2.2), получаем:

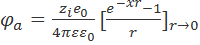. (3.2.4)

Для определения предела можно воспользоваться правилом Лопиталя или же разложить экспоненту в ряд. В результате находим, что предел выражения в квадратных скобках равен –х и, следовательно,

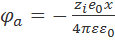. (3.2.5)

Сравнение формул (3.2.3) и (3.2.5) показывает, что ионная атмосфера оказывает на центральный ион такое же влияние, какое оказывала бы на него тонкая сферическая оболочка, имеющая заряд – z_ie₀ и расположенная на расстоянии 1/ъ от точечного центрального иона (рис. 3.1, в). Величина 1/x называется радиусом ионной атмосферы. Наконец, основываясь на аналогии формул (3.2.3) и (3.2.5), взаимодействие центрального иона с ионной атмосферой можно свести к кулоновскому взаимодействию двух ионов с зарядами z_ie₀ и –z_ie₀, находящихся друг от друга нарасстоянии 1/x (рис. 3.1,г). Энергия такого взаимодействия, как следует из уравнения (2.2.5), равна 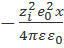и поровну распределяется между двумя ионами. Таким образом, изменение энергии центрального иона за счет его взаимодействия с ионной атмосферой составляет

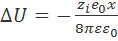. (3.2.6)

Формулу (3.2.6) можно получить также двумя другими способами. В первом из них, описанном в оригинальной работе П. Дебая и Э. Хюккеля, ∆U рассчитывали на основе мысленного процесса заряжения центрального иона и всех ионов, входящих в ионную атмосферу. При этом в процессе заряжения учитывалось перераспределение ионов, возникающее благодаря их электростатическому взаимодействию. Работа заряжения, рассчитанная этим способом (процесс заряжения по Дебаю), относилась ко всем ионам системы, а потому для нахождения величины ∆U ее нужно было продифференцировать по числу ионов данного вида i.

Во втором способе, который получил название процесса заряжения по Гюнтельбергу, предполагалось, что процесс мысленного заряжения ионов не сопровождается их перераспределением (т.е. что ионы уже до заряжения приобрели окончательное распределение, характерное для заряженной ионной атмосферы).

Этот способ эквивалентен процессу заряжения конденсатора, состоящего из центрального иона и окружающей его сферической оболочки с постоянным радиусом 1/х. Работа заряжения по методу Гюнтельберга сразу дает величину ∆U.

Следует подчеркнуть, что различные способы расчета изменения энергии центрального иона вследствие его взаимодействия с ионной атмосферой дают совпадающие результаты лишь при выполнении соотношения

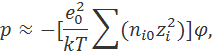
В условиях нелинейной зависимости ρ от ϕ различные способы расчета ∆U приводят к разным результатам.

Теория Дебая-Хюккеля

Используя выражение для коэффициента активности, можно рассчитать все парциальные моляльные термодинамические характеристики раствора (моляльную энтропию, мольный объем, теплоемкость, сжимаемость, термическое расширение и т. д.) при низких концентрациях. Теория Дебая-Хюккеля позволила предсказать эффект выделения теплоты при разбавлении растворов электролитов, вызванный тем, что при разбавлении уменьшается взаимодействие между ионами. В разбавленных растворах теплота разбавления по этой теории должна быть пропорциональна 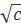, что было подтверждено на опыте. Учитывая, что предельный закон не содержит эмпирических параметров, отмеченные успехи теории Дебая-Хюккеля следует признать весьма значительными. Однакo с увеличением концентрации расхождение между теорией и опытом становится все более существенным.

Справедливость теории Дебая-Хюккеля только в разбавленных растворах (первое приближение этой теории) обусловлена следующими причинами:

1. Предположение о том, что заряд ионов размазан (непрерывен) в ионной атмосфере, выполняется лишь при условии, что можно пренебречь собственным объемом ионов, т.е. в достаточно разбавленных растворах. Только в этих условиях справедливо уравнение Пуассона, положенное в основу теории Дебая-Хюккеля.

2. Распределение Больцмана с дополнительным условием z_ie₀ϕ << kT также справедливо только в разбавленных растворах. Используя формулу (3.2.1) при r =1/x и выражение, приходим к выводу, что в водных растворах 1,1-валентного электролита при 25°С это неравенство выполняется при с 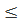0,01 моль/л. При более низких ε граничное значение смещается в область более низких концентраций (например, в бутаноле с 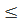0,0003 моль/л).

3. В теории Дебая-Хюккеля не учитывается изменение диэлектрической проницаемости раствора по сравнению с диэлектрической проницаемостью растворителя. В действительности величина ε уменьшается, так как диполи растворителя ориентируются по полю, создаваемому ионами (эффект диэлектрического насыщения). В разбавленных растворах этот эффект можно не учитывать, так как доля растворителя, связанного ионами, мала по сравнению с общим количеством растворителя.

4. Предельный закон Дебая-Хюккеля получен при рассмотрении ионов в виде математических точек. Очевидно, что такое допущение справедливо только в разбавленных растворах, когда можно пренебречь собственным объемом ионов.

5. Теория Дебая-Хюккеля учитывает только кулоновское ион-ионное взаимодействие и игнорирует другие виды взаимодействий (например, ион-дипольное взаимодействие, образование ассоциатов, комплексов и т. д.).

Во втором приближении П. Дебай и Э. Хюккель учли собственные размеры ионов, что позволило расширить диапазон концентраций ее применимости. Окончательно уравнение для среднего коэффициента активности приобретает вид:

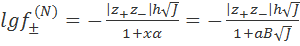, (3.3.1)