Химическое равновесие. Константа равновесия
Все химические реакции можно разбить на две группы: необратимые и обратимые реакции. Необратимые реакции протекают до конца — до полного израсходования одного из реагирующих веществ. Обратимые реакции протекают не до конца: при обратимой реакции ни одно из реагирующих веществ не расходуется полностью. Это различие связано с тем, что необратимая реакция может протекать только в одном направлении. Обратимая же реакция может протекать как в прямом, так и в обратном направлениях.
Например, взаимодействие между цинком и концентрированной азотной кислотой протекает согласно уравнению:
Zn + 4HNO3 → Zn(NO3)2 + 2NO2 ↑+ 2Н2О
При достаточном количестве азотной кислоты реакция закончится только тогда, когда весь цинк растворится. Кроме того, если попытаться провести эту реакцию в обратном направлении — пропускать диоксид азота через раствор нитрата цинка, то металлического цинка и азотной кислоты не получится — данная реакция не может протекать в обратном направлении. Таким образом, взаимодействие цинка с азотной кислотой — необратимая реакция.
Например, синтез аммиака протекает согласно уравнению:
N2 + 3 Н2 ↔ 2 NН3
Если смешать один моль азота с тремя молями водорода, осуществить в системе условия, благоприятствующие протеканию реакции, и по истечении достаточного времени произвести анализ газовой смеси, то результаты анализа покажут, что в системе будет присутствовать не только продукт реакции (аммиак), но и исходные вещества: азот и водород. Если теперь в те же условия в качестве исходного вещества поместить не азото-водородную смесь, а аммиак, то можно будет обнаружить, что часть аммиака разложится на азот и водород, причем конечное соотношение между количествами всех трех веществ будет такое же, как в том случае, когда исходили из смеси азота с водородом. Таким образом, синтез аммиака - обратимая реакция.
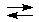
В уравнениях обратимых реакций вместо знака равенства можно ставить стрелки; они символизируют протекание реакции как в прямом, так и обратном направлениях.
На рис. 14 показано изменение скоростей прямой и обратной реакций с течением времени. Вначале, при смешивании исходных веществ, скорость прямой реакции велика, а скорость обратной реакции равна нулю. По мере протекания реакции исходные вещества расходуются и их концентрации падают. В результате этого уменьшается скорость прямой реакции.
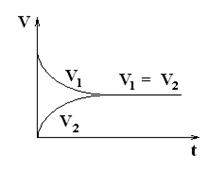
Рисунок 14. Изменение скорости прямой (v1) и обратной (v2) реакций с течением времени
Одновременно появляются продукты реакции и их концентрация возрастает. Вследствие этого начинает идти обратная реакция, причём ее скорость постепенно увеличивается. Когда скорости прямой и обратной реакций становятся одинаковыми, энтальпийный (ΔН) и энтропийный (ΔS) факторы (две противоположные тенденции) уравновешивают друг друга, т.е.
∆Н = Т • ∆S
В этом случае соблюдается уравнение
∆G = 0,
которое является термодинамическим условием химического равновесия. Так, в последнем примере устанавливается равновесие между азотом, водородом и аммиаком. Химическое равновесие – динамическое равновесие.
 Таким образом, химическое равновесие представляет собой динамическое состояние системы, при котором скорость прямой и обратной реакции равны и постоянны.
Таким образом, химическое равновесие представляет собой динамическое состояние системы, при котором скорость прямой и обратной реакции равны и постоянны.
Например, реакция N2 + 3 Н2 2 NН3. Реакцию, протекающую слева направо (→), называют прямой и обозначают v1, реакцию, протекающую справо налево (←), называют обратной и обозначают v2. Кинетическим условием химического равновесия является равенство v1= v2., термодинамическое условие равенства ∆G = 0, неравенство ∆G < 0 отвечает неравенству v1>v2, при этом самопроизвольно протекает прямая реакция, неравенство ∆G > 0 отвечает неравенству v1 < v2, при этом самопроизвольно протекает обратная реакция.
Говоря о равновесии, подчеркивают, что при равновесии протекают и прямая, и обратная реакции, но их скорости одинаковы, вследствие чего изменений в системе не заметно. В условиях химического равновесия концентрации исходных веществ и продуктов реакции не изменяются во времени и называются равновесными, обозначаются символом вещества в квадратных скобках: [Cl2], [Y2], [Н2О] и т.п.
Количественной характеристикой химического равновесия служит величина, называемая константой химического равновесия. Рассмотрим константу химического равновесия процесса
 аА + bB cC + dD
аА + bB cC + dD
для этого процесса изменение стандартной энергии Гиббса запишется:
ΔG0 = -RT ln ([C]c[D]d/ [A]a [B]b ),
где ΔG0 – изменение стандартной энергии Гиббса, R – универсальная газовая постоянная, Т – температура, [C]c ,[D]d, [A]a, [B]b – равновесные молярные концентрации продуктов реакции и исходных веществ соответственно, в степенях их стехиометрических коэффициентов.
Выражение в скобках получило название константы химического равновесия.
Константа химического равновесия – отношение произведения равновесных концентраций (или равновесных парциальных давлений) продуктов реакции к произведению равновесных концентраций исходных веществ (или равновесных парциальных давлений) в степенях их стехиометрических коэффициентов.
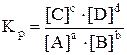
Это уравнение является вариантом математического выражения закона действующих масс, открытого норвежскими учеными К. Гульдбергом и П. Вааге (1867). Константа химической реакции не зависит от концентрации реагентов и может быть рассчитана, если известно стандартное значение энергии Гиббса
Кр = exp(–ΔG0/RT)
Химическое равновесие можно сместить, изменяя условия протекания реакции.
Принцип Ле-Шателье:
Если на систему, находящуюся в равновесии, оказывается внешнее воздействие, равновесие смещается в направлении протекания реакции, ослабляющей это воздействие.
Рассмотрим 3 случая принципа Ле-Шателье.
1) Влияние состава реакционной смеси.
При увеличении концентраций (парциальных давлений) исходных веществ или при уменьшении концентраций продуктов реакции равновесие смещается в сторону протекания прямой реакции (вправо).
При увеличении концентраций продуктов реакции или уменьшении концентраций исходных веществ равновесие смещается в сторону протекания обратной реакции (влево).
2) Влияние температуры.
При увеличении температуры равновесие смещается в сторону протекания эндотермическойреакции (DН > 0).
При уменьшении температуры равновесие смещается в сторону протекания экзотермического процесса (DН < 0).
3) Влияние общего давления в системе.
При увеличении общего давления (уменьшении объема) равновесие смещается в сторону протекания той реакции, при которой уменьшается количество газообразных веществ (в сторону уменьшения суммарного объема газов).
Например, для реакции N2 + 3H2 ↔ 2NH3, где DH<0
1. Константа равновесия зависит от температуры
ln Кр= -ΔH0/RT + ΔS0/R
или
Кр = exp(-ΔH0/RT) • exp(ΔS0/R)
Если ΔН0, ΔS0 независимы от температуры, то производная логарифма константы равновесия по температуре будет:
(d ln Кр /dT ) = ΔH0/RT2
таким образом, Кр убывает с уменьшением температуры и Кр возрастает с увеличением температуры.
При возрастании температуры для реакции синтеза аммиака равновесие смещается влево.
2. Увеличение давления.
Слева 4 моль газообразного вещества, а справа 2. Следовательно, равновесие сместится вправо.
3. Увеличение концентрации азота – равновесие сместится вправо.

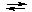 Пример 50. Реакция идет по уравнению 4HCl + O2 2H2O + 2Cl2. Через некоторое время после начала реакции концентрации участвующих в ней веществ были [HCl] =0,75 кмоль/м3, [O2] = 0,42 кмоль/м3, [Cl2] = 0,20 кмоль/м3. Какими были концентрации этих веществ в начале реакции?
Пример 50. Реакция идет по уравнению 4HCl + O2 2H2O + 2Cl2. Через некоторое время после начала реакции концентрации участвующих в ней веществ были [HCl] =0,75 кмоль/м3, [O2] = 0,42 кмоль/м3, [Cl2] = 0,20 кмоль/м3. Какими были концентрации этих веществ в начале реакции?
Дано: 4HCl + O2 2H2O + 2Cl2
[HCl] =0,75 кмоль/м3, [O2] = 0,42 кмоль/м3, [Cl2] = 0,20 кмоль/м3.
Найти: С0(HCl), С0(O2), С0(Cl2) - ?
Решение:1.Исходная концентрация хлора в начале реакции была равна нулю, тогда согласно уравнению реакции:
 4HCl + O2 2H2O + 2Cl2
4HCl + O2 2H2O + 2Cl2
Δ[O2] было израсходовано в 2 раза меньше чем образовалось хлора (0,20/2) кмоль/м3,
Δ[HCl] было израсходовано в 2 раза больше чем образовалось хлора (0,20•2) кмоль/м3
2.Находим исходные концентрации заданных веществ:
С0(HCl) = С кон (HCl) +Δ[HCl] =0,75 + 0,20•2=1,15 (кмоль/м3)
С0(O2) = С кон(O2) +Δ[O2] =0,42 + 0,20/2=0,52 (кмоль/м3)
С0(Cl2) = 0 (кмоль/м3)
Ответ: С0(HCl), С0(O2), С0(Cl2) веществ в начале реакции были соответственно: 1,15 кмоль/м3, 0,52 кмоль/м3, 0 кмоль/м3.
Пример 51.Вычислить, используя правило Вант-Гоффа, на сколько градусов нужно повысить температуру, чтобы скорость реакции возросла в 80 раз. Температурный коэффициент скорости реакции равен 3.
Дано: vt 2/ vt 1 =80; g = 3.
Найти: Δ t - ?
Решение:1.Согласно закону Вант-Гоффа:
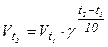
где 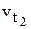 - скорость реакции при t2,
- скорость реакции при t2,
g - коэффициент Вант-Гоффа, показывающий во сколько раз увеличится скорость реакции при увеличении температуры на 10 градусов.
Тогда: 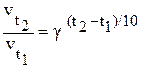 , подставляем заданные величины
, подставляем заданные величины 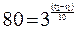 ,
,
2.Логарифмируем это уравнение:
lg80 = [( t2 – t1)/10] • lg3; Δt = t2 – t1= lg80/0,048= 1,90/0,048 = 39,8 (0C)
Ответ:чтобы скорость заданной реакции возросла в 80 раз, необходимо температуру реакции повысить примерно на 40 градусов.
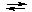 Пример 52.Для реакцииN2 + 3 Н2 2 NН3 опытным путем были определены костанты скорости прямой реакции при 716 К – 0,0067, а при 718К – 0,1059. Определить энергию активации данной реакции.
Пример 52.Для реакцииN2 + 3 Н2 2 NН3 опытным путем были определены костанты скорости прямой реакции при 716 К – 0,0067, а при 718К – 0,1059. Определить энергию активации данной реакции.
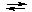 Дано: N2 + 3 Н2 2 NН3
Дано: N2 + 3 Н2 2 NН3
Т2 = 718 K; Т1 = 716 K; К2 = 0,1059; К1 = 0,0067.
Найти: Еа - ?
Решение: 1. Используем уравнение Аррениуса для двух температур:
ln К2/К1 = (Еа /R)•(1/Т1 - 1/Т2),
где К2, К1 –константы скорости при Т2,Т1, соответственно.
Или 2,303•lgК2/К1 = (Еа /R)•(1/Т1 - 1/Т2),
Еа –энергия активации процесса, Дж/моль,
R – газовая постоянная, Дж/(моль•К)
2. Выражаем из уравнения Аррениуса изменение энергии активации
Еа = R•2,303•lgК2/К1 • 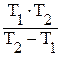
 Еа = 8,314•2,303•lg(0,1059/0,0067) • 257044=9795,6 (кДж/моль)
Еа = 8,314•2,303•lg(0,1059/0,0067) • 257044=9795,6 (кДж/моль)
Ответ: энергии активации реакцииN2 + 3Н2 2NН3 составило 9795,6 кДж/моль.
 Пример 53. При нагреавнии водорода с йодом в замкнутом сосуде до 717К протекает реакция Н2 + I2 2HI. Равновесная смесь при этой температуре содержит 5,64 кмоль йодистого водорода, 0,12 кмоль йода и 5,28 кмоль водорода. Вычислить Кр указанной реакции, а также исходные количества ввеществ йода и водорода.
Пример 53. При нагреавнии водорода с йодом в замкнутом сосуде до 717К протекает реакция Н2 + I2 2HI. Равновесная смесь при этой температуре содержит 5,64 кмоль йодистого водорода, 0,12 кмоль йода и 5,28 кмоль водорода. Вычислить Кр указанной реакции, а также исходные количества ввеществ йода и водорода.
 Дано: Н2 + I2 2HI
Дано: Н2 + I2 2HI
n(HI) = 5,64 кмоль; n(Н2) = 5,28 кмоль; n(I2) = 0,12 кмоль;T = 717 K.
Найти: Кр, n 0(Н2), n 0(I2)
Решение: 1. Так как константа химического равновесия – отношение произведения равновесных концентраций (или равновесных парциальных давлений) продуктов реакции к произведению равновесных концентраций исходных веществ (или равновесных парциальных давлений) в степенях их стехиометрических коэффициентов, то, константа равновесия для реакции
Н2 + I2 ↔2 HI будет записываться так
Кр =[HI]2 /([Н2]•[I2])
По условию задачи, данная реакция идет без изменения объема, тогда выражение константы равновесия вместо молярных концентраций веществ можно подставить количества веществ:
Кр = 5,642/(0,12•5,28) =50,19
2.Определяем исходные количества йода и водорода. По уравнению реакции 1 кмоль Н2 и еще 1 кмоль I2 расходуется на образование 2 кмолей HI. Так как образовалось к моменту равновесия 5,64 кмоль HI, то к этому же моменту израсходуется (5,64/2) Н2 и столько же прореагирует I2. Рассчитываем начальные количества веществ:
n 0(I2) = 5,64 /2 + 0,12 =2,94 (кмоль)
n 0(Н2) =5,64 /2 +5,28= 8,1 (кмоль)
Ответ: константа равновесия для заданной реакции составит 50,19, начальные количества веществ n 0(I2) = 2,94 (кмоль), n 0(Н2) = 8,1 (кмоль).
Комплексная задача № 10
В замкнутом технологическом режиме протекает процесс, указанный в варианте задания (табл. 24).
Для указанного процесса записать и рассчитать:
1. Математическое выражение для скорости прямой и обратной реакции;
2. Вычислить, используя правило Вант-Гоффа, на сколько градусов нужно повысить температуру, чтобы скорость реакции возросла в 50 раз. Температурный коэффициент скорости реакции равен 2,5;
3. Выражение для расчета Кр указанной реакции в общем виде.
Таблица 23
Варианты заданий
| № п/п | Химический процесс | № п/п | Химический процесс |
| 1. | C6H6(ж) + O2(г) ⇄ CO2(г) + H2O(г). | 21. | CH3OH(ж) + O2(г) ⇄ CO2(г) + H2O(ж) |
| 2. | NH3(г) + O2(г) ⇄ N2(г) + Н2О(ж); | 22. | C2H2(г) + O2(г) ⇄ СO2(г) + H2O(ж) |
| 3. | NH3(г) + O2(г) ⇄ NO(г) + H2O(ж); | 23. | H2(г) + CO2(г) ⇄ CO(г) + H2O(ж) |
| 4. | NH3(г) + O2(г) ⇄ N2(г) + H2O(ж); | 24. | CS2(г) + O2(г) ⇄ CO2(г) + SO2(г) |
| 5. | HCl(г) + O2(г) ⇄ H2O(г) + Сl2(г); | 25. | O2(г) ⇄ O3(г) |
| 6. | PbS(кр) + O2(г) ⇄ PbO(кр) + SO2(г). | 26. | Н2 (г) + С(к) = СН4 (г) |
| 7. | CO(г) + H2(г) ⇄ CH3OH(ж); | 27. | Fe3O4(кр) + CO(г) ⇄ FeO(кр) + CO2(г); |
| 8. | PCl5(г) ⇄ PCl3(г) + Сl2(г) | 28. | C2H5OH(ж) + O2(г) ⇄ CO2(г) + H2O(ж) |
| 9. | СН4(г) + Н2О(г) = СО(г) + 3Н2(г) | 29. | РН3(г) + О2(г) ⇄ Р2О5(к) + Н2О(ж) |
| 10. | NO2(г) ↔ N2O4(г) | 30. | Н2(г) + Сl2(г) = 2 HCl(г) |
| 11. | O2(г) + 2 H2S(г) = 2 Н2О(ж) + 2 SO2(г) | 31. | NО2(г) + SO2(г) ⇄NO(г) + SO3(г) |
| 12. | I2(г) + H2S(г) = 2HI (г) + S(к) | 32. | Сl2(г) +2HI(г) = I2(г) + 2HCl(г) |
| 13. | H2S(г) + O2(г) ⇄ SO2(г) + Н2O(г) | 33. | N2Н4(ж) + O2(г) ⇄ N2(г) + Н2O(г) |
| 14. | C2H2(г) ⇄ C6H6(г) | 34. | CH4(г) + 4 Cl2(г) = ССl4(г) + 4 НCl(г) |
| 15. | Н2(г) + I2(г) = 2 HI (г) | 35. | C3H7OH(ж) + O2(г) ⇄ CO2(г) + H2O(ж) |
| 16. | Ag2О(т) + CО(г) ⇄ Ag(т) + CО2(г). | 36. | C6H5СН3(ж) + O2(г) ⇄ CO2(г) + H2O(г) |
| 17. | PbS(т) + O3(г) ⇄ PbSO4(т) + O2(г). | 37. | C3H4(г) + H2(г) ↔ C2H6(г) |
| 18. | Сl2(г) + Н2О(ж) ⇄ НСl(ж) + НСlО(ж) | 38. | C2H4(г) + Cl2(г) ↔ C2H4Cl2(г) |
| 19. | C2H2(г) + H2(г) ↔ C2H4(г) | 39. | C2H4(г) + Br2(г) ↔ C2H4Br2(г) |
| 20. | СO(г) + Сl(г) ↔ СОСl2(г) | 40. | C6H8(ж) + Cl2(г) ↔ C6H8Cl2(ж) |
ПРИЛОЖЕНИЯ
Приложение 1
Таблица 1
Варианты заданий для выполнения контрольной работы
| № варианта | Комплексная задача | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - |
Продолжение таблицы 1
| № варианта | Комплексная задача | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - |
Окончание таблицы 1
| № варианта | Комплексная задача | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - | |||||||||
| - | - |
Приложение 2
Таблица 1
